第三章 复习与提高
A 组
1.向水面上扔一个石块,形成如图 3–1 所示的波形,已知相邻实线间的距离等于一个波长,不考虑水波的反射,试大致画出水波通过图 3–1 甲的孔 A 和 B 以及遇到图 3–1 乙中障碍物 C 和 D 之后的传播情况。
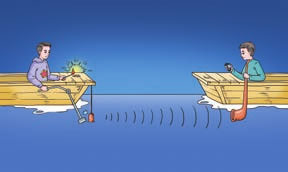
2.第一次测定声音在水中的传播速度是 1827 年在日内瓦湖上进行的,现有两位同学模拟当年情景(图 3–2):两条船相距 14 km,一位同学在一条船上敲响水里的一口钟,同时点燃船上的火把使其发光;另一条船上的同学在看到火把发光后 10 s,通过水里的听音器听到了水下的钟声。试根据这些数据计算水中的声速。
3.图 3–3 的横波正在沿 x 轴的正方向传播,波速为 0.5 m/s,分别画出经过 1 s 和 4 s 后的两个波形图。
4.一列简谐横波在 t = 0 时的波形图如图 3–4 所示。介质中 x = 2 m 处的质点 P 沿 y 轴方向做简谐运动的表达式为 y = 10sin(5πt)(y 的单位是 cm)。
(1)由图确定这列波的波长 λ 与振幅。
(2)求出这列波的波速。
(3)试判定这列波的传播方向。
5.某波源 S 发出一列简谐横波,波源 S 的振动图像如图 3–5 所示。在波的传播方向上有 A、B 两点,它们到 S 的距离分别为 45 m 和 55 m。测得 A、B 两点开始振动的时间间隔为 1.0 s。
(1)求这列波的波长 λ。
(2)当 B 点离开平衡位置的位移为 6 cm 时,A 点离开平衡位置的位移是多少?
B 组
1.如图 3–6 甲,两列沿相反方向传播的横波,形状相当于正弦曲线的一半,上下对称,其振幅和波长都相等。它们在相遇的某一时刻会出现两列波“消失”的现象,如图乙。请判断:从此时刻开始 a、b 两质点将向哪个方向运动?
2.振源 A 从 0 时刻开始带动细绳上各点上下做简谐运动,振幅为 0.2 m。0.4 s 时绳上形成的波形如图 3–7 所示。规定向上为质点振动位移的正方向,试画出 A 点的振动图像。
3.图 3–8 中的 a 是一列正弦波在某时刻的波形曲线,b 是 0.2 s 后它的波形曲线。试求这列波可能的传播速度。
4.如图 3–9,S 点是波源,振动频率为 100 Hz,产生的简谐波向右传播,波速为 80 m/s。波在传播过程中经过 P、Q 两点,已知 SP 为 4.2 m,SQ 为 5.4 m。
(1)在某一时刻 t,当 S 点通过平衡位置向上运动时,P 点和 Q 点是处于波峰还是处于波
谷,或者处于其他位置?
(2)取时刻 t 为时间的起点,分别作出 S、P、Q 三点的振动图像。
5.在学校运动场上 50 m 直跑道的两端,分别安装了由同一信号发生器带动的两个相同的扬声器。两个扬声器连续发出波长为 5 m 的声波。一同学从该跑道的中点出发,向某一端点缓慢行进 10 m。求在此过程中他听到扬声器声音由强变弱的次数?
6.如图 3–10,一列简谐横波在 x 轴上传播,图甲和图乙分别为 x 轴上 a、b 两质点的振动图像,且 xab 为 6 m。试求出这列波的波长与波速?
7.两列简谐横波分别沿 x 轴正方向和负方向传播,两波源分别位于 x = − 0.2 m 和 x = 1. 2 m 处,两列波的波速均为 0.4 m/s,波源的振幅均为 2 cm。图 3–11 为 0 时刻两列波的图像,此刻平衡位置在 x = 0.2 m 和 x = 0.8 m 的 P、Q 两质点刚开始振动。质点 M 的平衡位置处于 x = 0.5 m 处。
(1)求两列波相遇的时刻。
(2)求 1.5 s 后质点 M 运动的路程。
“复习与提高”参考答案与提示
A 组共 5 道习题。第 1 题考查发生明显衍射现象的条件,第 2 题让学生了解早期测量声速的方法,第 3 题结合波速、波长与周期关系画波的图像,第 4、5 题分别考查由质点振动方程和质点振动图像获取波速、波长、周期、振幅等物理量及振动与波动的关系。
B 组共 7 道习题。第 1 题考查波的独立传播与叠加原理,第 2 题考查由波形图画出质点振动图像,第 3 题是根据波在两个时刻的波形图来计算波速的问题,第 4 题是根据题目信息确定质点所处的位置及推理质点振动情况,第 5 题理论结合实际,考查波的干涉的定量计算,第 6 题根据两质点振动图像求波长和波速,第 7 题为机械波综合问题,主要考查波的干涉、波的叠加原理。
A 组
1.如图 3–8 所示。
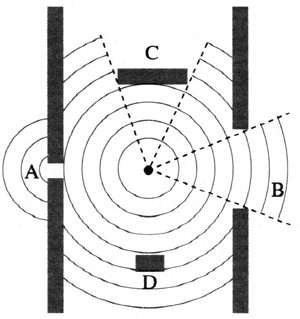
图 3–8
提示:A 孔与 D 障碍物尺寸比较小,波传播时容易绕到背后“阴影”区,B 孔与 C 障碍物尺寸较大,不容易发生明显的衍射现象,波传播时几乎沿直线传播。
2.1.4×103 m/s
3.1 s 后波形如图 3–9 中虚线所示,4 s 后波形如图中实线所示。
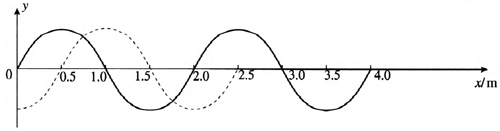
图 3–9
4.(1)振幅 A = 10 cm,波长 λ = 4 m
(2)10 m/s
(3)波向 x 正方向传播
5.(1)20 m
(2)− 5 cm
B 组
1.a 向下,b 向上
2.如图 3–10 所示。
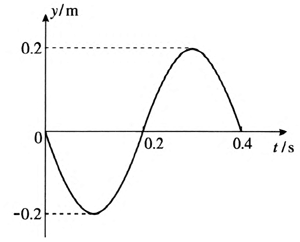
图 3–10
3.若波沿 x 轴正方向传播,波速是(20n + 5)m/s,n = 0,1,2,…;若波沿 x 轴负方向传播,波速是(20n + 15)m/s,n = 0,1,2…
提示:若波沿 x 轴正方向传播,波传播的距离 x = nλ + \(\dfrac{\lambda }{4}\),波速 v = \(\dfrac{x}{t}\) = (20n + 5)m/s,n = 0,1,2,…;若波沿 x 轴负方向传播,波传播的距离 x = nλ + \(\dfrac{{3\lambda }}{4}\),波速 v = \(\dfrac{x}{t}\) = (20n + 15)m/s,n = 0,1,2,…。
4.(1)P 在波谷,Q 在波峰;
(2)如图 3–11 所示。
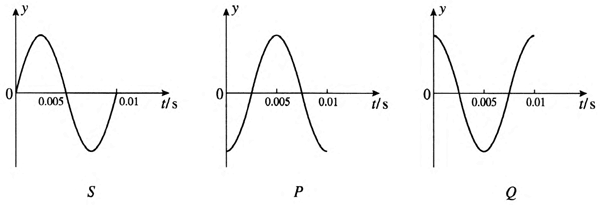
图 3–11
5.提示:设该同学缓慢行进时距最近的扬声器的距离为 x(15 m≤ x ≤25 m),则该同学距最远的扬声器的距离为 50 − x,该同学听不到声音的条件是(50 − x)− x = \(\dfrac{\lambda }{4}\)(2n − 1),n = ±1,±2,±3,…代入数据解得 \(\dfrac{1}{2}\) ≤ n ≤ \(\dfrac{9}{2}\),即 n = 1,2,3,4,故他听到扬声器声音由强变弱的次数为 4 次。
6.设由 a 指向 b 为 x 轴正方向,若波沿 x 轴正方向传播,波长 λ = \(\dfrac{{24}}{{4n + 1}}\) m,波速 v = \(\dfrac{\lambda }{T}\) = \(\dfrac{{6}}{{4n + 1}}\) m/s;若波沿 x 轴负方向侍播,波长 λ = \(\dfrac{{24}}{{4n + 3}}\) m,波速 v = \(\dfrac{\lambda }{T}\) = \(\dfrac{{6}}{{4n + 3}}\) m/s。
提示:由振动图像无法比较 a、b 两质点振动的先后,所以无法判断波的传播方向。若波沿 x 轴正方向传播,由振动图像读出 t = 0 时刻“质点经过平衡位置向下运动,而 b 位于波峰,结合波形图得到 xab = nλ + \(\dfrac{\lambda }{4}\)(n = 0,1,2,…),即波长 λ = \(\dfrac{{24}}{{4n + 1}}\) m,波速 v = \(\dfrac{\lambda }{T}\) = \(\dfrac{{6}}{{4n + 1}}\) m/s。同理可知,若波沿 x 轴负方向传播,波长 λ = \(\dfrac{{24}}{{4n + 3}}\) m,波速 v = \(\dfrac{\lambda }{T}\) = \(\dfrac{{6}}{{4n + 3}}\) m/s。
7.(1)0.75 s;(2)12 cm
提示:(1)两列简谐波的波前相距 s = 0.6 m,设两列波经时间 t 相遇,则 s = 2vt,可解得 t = 0.75 s。
(2)两列波经 t = 0.75 s 相遇在 PQ 的中点 M,所以 M 点在 t = 0.75 s 时开始振动。两列波的周期 T = \(\dfrac{\lambda }{v}\) = 1.0 s,由图可知,两列波同时到达 M 点时,引起质点振动的方向均沿 y 轴负方向。所以,两列波在 M 点的振动加强,即 M 点的振幅 A′ =2A = 4 cm。t = 1.5 s 时,M 点振动了 Δt = 0.75 s,即 \(\dfrac{3}{4}\)T。根据简谐运动的周期性,M 点运动的路程 s = 3A′ = 12 cm。
发布时间:2020/9/12 下午8:51:41 阅读次数:2842
