第一章 第 3 节 位置变化快慢的描述——速度
生活和科学研究中经常需要知道物体运动的快慢和方向,你还记得初中是怎样描述物体运动快慢的吗?运动员在比赛中的不同时段,运动的快慢一样吗?

不同的运动,位置变化的快慢往往不同,也就是说,运动的快慢不同。我们已经用位移来表示位置的变化,那么,怎样比较物体运动的快慢呢?物理学中用位移与发生这段位移所用时间之比表示物体运动的快慢,这就是速度(velocity)。
速度通常用字母 v 表示,如果在时间 Δt 内物体的位移是 Δx ,它的速度就可以表示为
\[v = \frac{{\Delta x}}{{\Delta t}}\]
在国际单位制中,速度的单位是米每秒,符号是 m/s 或 m·s−1。常用的单位还有千米每时(km/h 或 km·h−1)、厘米每秒(cm/s 或 cm·s−1)等。
速度是矢量,它既有大小,又有方向。速度 v 的方向与时间 Δt 内的位移 Δx 的方向相同。
这里的速度和初中所学的速度含义不完全相同。
一般来说,物体在某一段时间内,运动的快慢通常是变化的。所以,由 \(\frac{{\Delta x}}{{\Delta t}}\) 求得的速度 v,表示的只是物体在
时间 Δt 内运动的平均快慢程度,叫作平均速度(average velocity)。
平均速度描述物体在一段时间内运动的平均快慢程度及方向。那么,怎样描述物体在某一时刻运动的快慢和方向呢?
可以设想,用由时刻 t 到 t + Δt 一小段时间内的平均速度来代替时刻 t 物体的速度,如果 Δt 取得小一些,物体在 Δt 这样一个较小的时间内,运动快慢的差异就不会太大。Δt 越小,运动快慢的差异就越小。当 Δt 非常非常小时,运动快慢的差异可以忽略不计,此时,我们就把 \(\frac{{\Delta x}}{{\Delta t}}\) 叫作物体在时刻 t 的瞬时速度(instantaneous velocity)。
匀速直线运动是瞬时速度保持不变的运动。在匀速直线运动中,平均速度与瞬时速度相等。
瞬时速度的大小通常叫作速率(speed)。汽车速度计不能显示车辆运动的方向,它的示数实际是汽车的速率(图 1.3–1)。日常生活中说到的“速度”,有时是指速率,要根据上下文判断。

测量纸带的平均速度和瞬时速度
测量平均速度 我们知道,用手拉通过打点计时器的纸带时,确定时间内纸带运动的信息就被记录下来,据此,可以计算纸带的运动速度。
图 1.3–2 是打点计时器打出的一条纸带示意图。若想计算实验时运动的纸带在 D、G 两点间的平均速度 v,只需测出 D、G 间的位移 Δx 和所用的时间 Δt,就可以算出平均速度
\[v = \frac{{\Delta x}}{{\Delta t}}\]
请根据上述方法,计算上节实验中运动的纸带某些点间的平均速度。
每隔 0.1 s (或更短)计算一次平均速度。
1.在图 1.3–2 中选取纸带上一点为起始点 0,后面每 5 个点取一个计数点,分别用数字 1,2,3,… 标出这些计数点;
2.测量各计数点到起始点 0 的距离 x,记录在表 1 中;
3.计算两相邻计数点间的位移 Δx,同时记录对应的时间 Δt;
4.根据 Δx 和 Δt 计算纸带在相邻计数点间的平均速度 v。
表 1 手拉纸带的位移和平均速度
| 位置 | 0 | 1 | 2 | 3 | 4 | … |
| x /m | ||||||
| Δx /m | ||||||
| Δt /s | ||||||
| v /(m·s−1) |
测量瞬时速度 如何测量运动物体在某一时刻或某一位置(例如图 1.3–2 中 E 点)的瞬时速度?
我们可以这样考虑:E 点在 D、G 两点之间,D、G 两点间的平均速度我们可以求出。如果不要求很精确,用这个平均速度粗略地代表 E 点的瞬时速度,也未尝不可。不过,如果把包含 E 点在内的间隔取得小一些,例如取图 1.3–3 中的 DF 线段,那么经过 D、F 两点所用的时间 Δt 就会变短,用两点间的位移 Δx 和时间 Δt 算出的平均速度代表纸带在 E 点的瞬时速度,就会精确一些。D、F 两点离 E 点越近,算出的平均速度越接近 E 点的瞬时速度。
D、F 两点间距离过小,测量误差会增大。所以,实际测量中要根据需要及所用仪器的情况,在要测量的点附近选取合适的位移和时间。请考虑此实验中产生误差的原因。
请根据上述测量瞬时速度的方法,计算上节实验中纸带上各计数点的瞬时速度。每隔 0.06 s 计算一次速度。
1.从纸带起始点 0 算起,后面每 3 个点取一个计数点;
2.测量各计数点到起始点 0 的距离 x,记录在表 2 中;
3.计算两相邻计数点间的位移 Δx,同时记录对应的时间 Δt;
4.根据 Δx 和 Δt 算出的速度值就可以代表在 Δx 这一区间内任意一点的瞬时速度。
将算出的各计数点的速度值记录在表 2 中。
表 2 手拉纸带的瞬时速度
| 位置 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| x /m | ||||||||
| Δx /m | ||||||||
| Δt /s | ||||||||
| v /(m·s−1) |
物体运动的速度随时间变化的情况可以用图像来直观表示。以时间 t 为横轴,速度 v 纵轴,坐标中的图像即为速度–时间图像或 v–t 图像。
在方格纸上建立直角坐标系,根据自己算出的手拉纸带的 v、t 数据,在坐标系中描点,练习画 v–t 图像。
图 1.3–4 甲是根据某同学的实测数据所描的点,从这些点的走向能够大致看出纸带运动速度的变化规律。如果用一条平滑的曲线来描出这些点,曲线所反映的情况就会与实际更加接近(图 1.3–4 乙)。
借助传感器与计算机测速度
随着信息技术的发展,中学物理的实验手段也在不断进步。用“位移传感器”把物体运动的位移、时间转换成电信号,经过计算机的处理,可以立刻在屏幕上显示物体运动的速度,自动绘制出物体运动的v-t图像(图1.3–5)。这样,同学们就可以用更多的时间和精力对物理过程进行分析。
图 1.3–6 是利用位移传感器测量速度的示意图。这个系统由发射器 A 与接收器 B 组成,发射器 A 能够发射红外线和超声波信号,接
收器 B 可以接收红外线和超声波信号。发射器 A 固定在被测的运动物体上,接收器 B 固定在桌面上或滑轨上。测量时 A 向 B 同时发射一个红外线脉冲和一个超声波脉冲(即持续时间很短的一束红外线和一束超声波)。B 接收到红外线脉冲开始计时,接收到超声波脉冲时停止计时。根据两者的时差和空气中的声速,计算机自动算出 A 与 B 的距离(红外线的传播时间可以忽略)。
经过短暂的时间 Δt 后,传感器和计算机系统自动进行第二次测量,得到物体的新位置。算出两个位置差,即物体运动的位移 Δx ,系统按照
\[v = \frac{{\Delta x}}{{\Delta t}}\]
算出速度 v,显示在屏幕上。所有这些操作都可以在不到 1 s 的时间内自动完成。
这样测出的速度是发射器 A 在时间 Δt 内的平均速度。然而 Δt 很短,通常设置为 0.02 s,所以 Δx 与 Δt 之比可以代表此刻发射器 A(即运动物体)的瞬时速度。
还有另外一种位移传感器,如图 1.3–7 所示。这个系统只有一个不动的小盒 C,工作时小盒 C 向被测物体 D 发出短暂的超声波脉冲,脉冲被运动物体反射后又被小盒 C 接收。根据发射与接收超声波脉冲的时间差和空气中的声速,可以得到小盒 C 与运动物体 D 的距离 x1、x2 以及 Δx 和 Δt,从而系统也能算出运动物体 D 的速度 v。
1.把纸带的下端固定在重物上,纸带穿过打点计时器,上端用手提着。接通电源后将纸带释放,重物便拉着纸带下落,纸带被打出一系列点,其中有一段如图 1.3–8 所示。
(1)图中所示的纸带,哪端与重物相连?
(2)怎样计算在纸带上打 A 点时重物的瞬时速度?说出你的理由。
2.图 1.3–9 是甲、乙两物体沿某一直线运动的 v–t 图像,至少从以下三个方面分别说明它们的速度是怎样变化的。
(1)物体是从静止开始运动还是具有一定的初速度?
(2)速度的大小变化吗?是加速还是减速?
(3)运动的方向是否变化?
3.汽车从制动到停止共用了 5 s。这段时间内,汽车每 1 s 前进的距离分别是 9 m、7 m、5 m、3 m、1 m(图1.3–10)。
(1)求汽车前 1 s、前 2 s、前 3 s、前 4 s 和全程的平均速度。在这五个平均速度中,哪一个最接近汽车刚制动时的瞬时速度?它比这个瞬时速度略大些,还是略小些?
(2)汽车运动的最后 2 s 的平均速度是多少?
教学目标和教学建议
1.教学目标
(1)通过抽象概括,理解速度的含义。知道速度的定义式、单位和方向。
(2)理解平均速度和瞬时速度的区别与联系,初步体会极限方法在研究物理问题中的应用和意义。知道匀速直线运动的特点及速率的含义。能在实际问题中正确辨析、应用以上关于速度的概念。
(3)会使用打点计时器测量平均速度和瞬时速度。认识如实记录数据、实事求是的重要性,培养科学的态度。
(4)理解 v−t 图像的含义,能用实验数据绘制 v−t 图像,并会根据 v−t 图像分析物体运动的速度随时间的变化。
(5)联系与速度有关的实例,体会物理学在生产和生活中的用途,增强物理学习的兴趣。
2.教材分析与教学建议
速度是描述物体运动的重要物理量,本节内容围绕速度概念的建立展开。教科书的内容安排是有层次的,具体表现为:首先通过“问题”引导学生回忆初中时如何描述物体运动的快慢,并且引导学生分析运动员在比赛中不同时段的运动快慢是否相同,这为引入瞬时速度做好了铺垫。
然后在分析的基础上,引导学生认识到为了描述物体的运动,不仅应该描述物体位置变化的多少,还要描述其快慢,这就需要建立速度的概念。为进一步精确描述物体的运动快慢,又引入了平均速度和瞬时速度的概念。最后,结合瞬时速度的概念,研究测量速度的方法以及描绘速度-时间图像的方法。本节的重点和难点是速度、平均速度和瞬时速度等概念的建立,以及通过实验测量速度及描绘 v−t 图像的方法。
速度是学生初中已有的概念,难点表现在对概念的重建和进阶学习上。由于位移和路程的不同,高中所学的速度概念与初中不同,教科书提醒学生注意这个差异,以比较的方法加深对新概念的理解。速度概念的深化还体现在矢量性上,继位移后再次学习和应用矢量的概念,逐步加强对矢量的认识。
平均速度过渡到瞬时速度的极限思想学生首次接触,因此是本节的另一个难点。学生对“Δt 非常非常小”的含义不一定理解得很清楚,教师可以用匀速直线运动作为过渡例子引导学生思考,学生一时不理解也不必强求,随着物理和数学知识的进一步学习,学生会逐渐加深对极限思想的理解。
速度的测量(包括拓展实验部分)是通过实验对位移、时间和速度概念的综合运用,对学生实验探究和科学思维能力要求较高,其中瞬时速度的测量再次用到极限思想,学生要体会理想条件(Δt 非常非常小)如何在实际测量(Δt 小到一定精度)中合理地实现。要引导学生认识到:从理论上讲,Δt 越小,物体在一段时间内的平均速度越接近某一位置或时刻的瞬时速度,但考虑到实际测量误差,当时间太短时,在这段时间内的位移也非常小,测量误差会增大,因此实际测量中应该根据实际需要和所使用的测量仪器的情况,选取合适的时间间隔。
在描绘 v−t 图像时,在坐标系中正确地描点和合理地绘制曲线是学生学习的重点和难点,教师要耐心指导,为后面应用 v−t 图像研究物理问题打下基础。
(1)问题引入
本节节前提出的问题是回忆初中怎样描述物体运动的快慢。
学生的速度概念在生活中有很多相关的感性认识,但这些认识不一定都科学、准确。此处教学设计要尽量在学生已有概念的基础上激发新的认知冲突,为下一步教学打下基础。
教学片段
速度概念的引入
教师可以让学生分析第 2 节实验中学生记录的数据或 x–t 图像,也可以演示百米赛跑或行人、自行车、汽车在相同时间内的运动情况,让学生思考分析这些运动有什么不同,用什么物理量描述这种不同。学生会指出上述物体运动的快慢不同,用速度可以表示物体运动的快慢。在此基础上教师可以展开如下教学过程:
师:初中学习的速度定义是什么?
生:路程与时间之比。
师:有两辆车从同一地点同时出发,经过长短不同的两条路径,同时到达一个终点,这段时间内两辆车位置变化的快慢相同吗?
生:两辆车在相同的时间内发生了相同的位移,所以位置变化的快慢相同。
师:还有两辆车从同一地点出发,一辆向东开,一辆向南开,路程与时间的比都是20 m/s,你认为它们的运动相同吗?位置变化快慢相同吗?
生:两辆车的运动方向不一样,它们的运动和位置变化的快慢应该是不同的。
师:我们研究物体运动的快慢,很多时候是要研究物体的位置随时间变化的快慢,此时应如何定义速度呢?
生:可以用位移与时间之比定义速度。
(2)速度
通过上面问题引入环节的讨论,学生意识到要用速度描述运动物体位位置变化的快慢,应该用位移与对应时间之比来定义速度,其定义式为 v = \(\frac{{\Delta x}}{{\Delta t}}\)。
速度的单位学生初中已经学过,教师可以再明确一下速度的国际单位和常用单位及其换算关系。此处可以指出,速度单位是由位移和时间的单位复合而成的,学生学过的很多物理量的单位也是复合单位(例如密度的单位是 kg/m3),它们的换算关系可以通过物理量之间的关系(例如密度等于物体质量与相应体积的之比)得出。通过教学让学生对物理量的单位及单位制的意义有初步的认识。
教科书指出这里讨论的速度和初中所学的略有不同,此处教师要明确速度定义的变化,不必急于强化新的概念。因为学生刚接触位移等矢量概念,要建立更全面的速度概念还需要经过一个累积和内化的过程。此时教师可以先从定义中速度与位移的关系出发,使学生明确速度的矢量性。
速度方向的教学是此处的重点。教师可以从学生的感性认识出发认识到物体速度方向即为运动方向,引导学生思考物体因运动产生位置变化,所以运动方向即位移方向,因而得出速度方向与位移方向一致的结论。对数学基础好的学生,也可以引导他们直接由速度定义式进行分析:Δx 是矢量、Δt 是标量,v = \(\frac{{\Delta x}}{{\Delta t}}\)也应是矢量,且速度 v 的方向应与位移 Δx 方向相同。
为加深学生对速度大小的感性认识,还可以让学生分组调查一些常见物体的运动速度。例如,光在真空中传播的速度,飞机、火车和轮船等交通工具行驶的速度,人走路或跑步的速度等。培养学生注重理论联系实际、关注社会发展的学习态度。
(3)平均速度和瞬时速度
实际生活中很多运动是速度随着时间发生变化的变速运动。教师可以结合实验或实际运动的视频等让学生分析和体会运动中速度的变化,在此基础上学生理解由 v = \(\frac{{\Delta x}}{{\Delta t}}\)求得的速度表示的是 Δt 这段时间内物体运动的平均快慢程度。要注意强调位移Δx与时间Δt的对应性。
在学习瞬时速度时,有的学生可能认为某一时刻物体的位移和时间间隔都是 0,t 时刻的速度无法计算。这是因为学生把物体固定在了一个点,而不是运动中经过这个点。教师可以跟学生解释,虽然现阶段学生所学的数学知识还不能很好地定量分析这个问题,但以后学习了微积分就能解决了,其方法的基础就是极限思想,数学与物理并不矛盾。
对运动快慢发生变化的物体,其平均速度和瞬时速度一般是不同的,教师可以引导学生思考有没有平均速度和瞬时速度相同的运动,从而得出匀速直线运动——物体运动过程中瞬时速度保持不变,平均速度和瞬时速度相等。
速度是矢量,瞬时速度的方向是物体运动的位移方向,其大小叫作速率。日常生活中提到的速度,有的时候并未明确其方向,因而指的是速率。教师可以通过让学生分析匀速圆周运动是否是匀速运动来辨析速度和速率概念的差异。
对于数学基础较好的学生,也可以应用位移-时间图像分析,由平均速度的极限得出瞬时速度的概念,可参考下面的教学片段。
教学片段
由 x−t 图像认识瞬时速度的概念
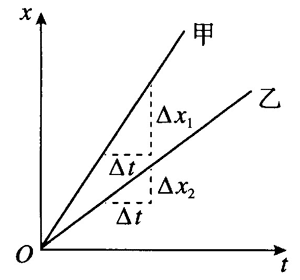
先让学生回忆上节学习的 x-t 图像并分析两个倾斜程度不同的 x−t 图像(图 1–5),由速度定义式 v=\(\frac{{\Delta x}}{{\Delta t}}\) 可知甲的速度大于乙的速度,而 \(\frac{{\Delta x}}{{\Delta t}}\) 又是图线的倾斜程度一斜率,从而引导学生得出 x−t 图像的斜率表示速度大小的结论。
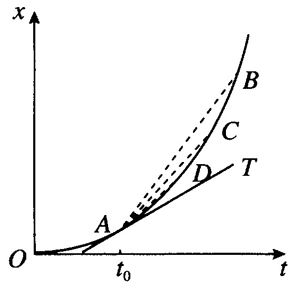
再请学生分析如图 1–6 所示的做变速直线运动物体的 x−t 图像。过 A 点的割线 AB 的斜率反映的是 AB 段内物体运动的平均速度,显然与 t0 时刻的运动快慢差异较大。缩短了与 A 点时间间隔的割线 AC,其斜率反映的是 AC 段内物体运动的平均速度,就比较接近 t0 时刻的运动快慢了。进一步缩短时间间隔的割线 AD 的斜率,更加接近 t0 时刻的运动快慢。当时间间隔取得非常非常小(趋近于 0)时,过 A 点的割线就会逼近过 A 点的切线 AT,而过 A 点的切线的斜率就准确地表示了 t0 时刻的运动快慢,即 t0 时刻的瞬时速度。
从上述推导过程可见,当时间间隔 Δt 非常非常小时,Δt 内的平均速度就可以表示 t 时刻的瞬时速度了。
瞬时速度概念建立过程的极限思想对学生来说有一定困难,教师可以通过引导学生对一些运动实例进行分析,逐步加深对瞬时速度概念的理解,可以安排下面的实验。
教学片段
测量滑块的平均速度和瞬时速度
如图 1–7 所示,让滑块沿倾斜的气垫导轨做加速运动。在滑块上固定不同长度的遮光片,若没有成品遮光片,可以用硬纸片自制成需要的宽度。测出每个遮光片通过光电门所用的一段时间间隔 Δt。
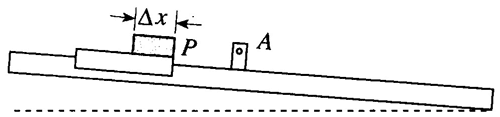
表 1–2 是某位老师采集的实验数据。当滑块从同一高度滑下,其前端 P 到达 A 点时的速度相等。滑块上装有宽度为 Δx 的不同遮光片,用光电门测量滑块上不同宽度的遮光片通过 A 点所需的时间 Δt,可以求出不同宽度的遮光片经过 A 点的平均速度。由表 1-2 中数据可知,在遮光片宽度小于 3.8 cm 之后,三组数据的平均速度都是 0.41 m/s。这说明时间间隔小到一定程度后,遮光片经过 A 点的过程中速度已无明显变化,遮光片全部通过 A 点的平均速庋就可以代表其前端 P 到达 A 点的瞬时速度,即 0.41 m/s。
表 1–2
|
Δx/m(遮光片的宽度) |
Δt/s |
v/(m·s−1) |
||
|
1 |
2 |
3 |
||
|
0.300 |
0.632 |
0.635 |
0.636 |
0.47 |
|
0.200 |
0.460 |
O.459 |
0.458 |
0.44 |
|
0.110 |
0.264 |
0.263 |
0.263 |
0.42 |
|
0.038 |
0.094 |
0.094 |
0.093 |
0.41 |
|
0.024 |
0.059 |
0.058 |
0.058 |
0.41 |
|
0.0086 |
0.021 |
0.021 |
0.021 |
0.41 |
实验将通过取 Δt 非常小时由平均速度求瞬时速度的方法,用实际例子展示出来,便于学生理解极限思想。
速度概念的含义很广泛,实际生活中的应用也很多,速度概念将随着学生学习内容的深入和能力提升逐步形成。
(4)速度的测量
与位移和时间不同,速度是一个间接测量量,要根据速度的定义,先测量位移和时间,再间接地计算出相应时间内的速度。教科书以打点计时器打出的纸带为例,分析了测量平均速度和瞬时速度的方法。二者并没有质的区别,关键是时间间隔选取的长短不同,反应物体运动快慢的精确程度也就不同。时间间隔足够小时,就可以用一段时间的平均速度代表这段时间内某时刻的瞬时速度。
这部分教学可以先引导学生设计测量物体运动速度的实验方案。学生经过查阅资料和讨论会发现,测量速度的基本原理还是应用速度的定义——位移与时间之比,这样就把速度的测量转化为位移和时间的测量。上一节学习了用打点计时器测量物体运动的位移和时间,因此此处的重点是如何应用打出的纸带来研究物体运动的平均速度和瞬时速度,教学过程可以参考下面的方案。
教学片段
速度的测量
教师引导学生思考如何应用实验打出的纸带来研究任意两点间的平均速度,例如图 1–8 中AD 或 DG 之间的平均速度。要求学生通过计算研究不同时间间隔内的平均速度是否相同,物体运动的快慢是否变化等。

学生通过测量某两点间的距离,用平均速度公式 v=\(\frac{{\Delta x}}{{\Delta t}}\) 求出不同时间间隔内的平均速度,发现平均速度是变化的,物体在做变速运动。
教师进一步引导学生思考如何求纸带上某点的瞬时速度,例如图中 D 点。时间间隔是否越短越淮确?
学生选取的 Δt 的大小和位置可能不同。有的学生从定义出发认为应该选取更短的 Δt,教师可以从位移测量精确程度的角度指导学生适当选取 Δt。有的学生选的 Δt 在待测点前,例如图中 BD 段;有的选包含待测点的一段,例如图中 CE 段;有的则选在待测点之后,例如图中 DF 段。教师可以引导学生比较各种选法求出的速度哪个更接近待测点的瞬时速度。
除了用打点计时器记录物体的位移和时间来测量物体的速度外,还有很多测量速度的方法和仪器。本节最后“拓展实验”中介绍了借助传感器与计算机测量速度的实验方法。传感器在生产、生活实际中应用广泛,在物理实验中也因其操作便捷、精度高而越来越普及,学生应尽早接触、学习和应用。因此建议有条件的学校可以由教师课堂演示或学生课后探究完成这个实验,没有条件的学校也应播放相关视频资料、讨论实验原理。虽然书中介绍的两种传感器用到红外线和超声波来测距,与打点计时器的测距方法不一样,但其根本的测速原理仍是应用公式 v = \(\frac{{\Delta x}}{{\Delta t}}\),通过测量一段时间内的位移,来求出这段时间的平均速度。又由于通常 Δt 很短,所以平均速度可视为物体的瞬时速度。需要指出的是,虽然与传感器配合使用的计算机软件可以直接显示 Δx、Δt 成物体的瞬时速度,教学中还是应让学生弄清实验原理和数据处理的方法。
(5)速度−时间图像
学生在上一节曾学习过位移−时间图像,此处描绘和分析速度−时间图像可以进一步巩固描绘物理图像的方法和提高通过图像研究物理规律的能力。同时要注意,在上节作图方法的基础上,教科书增加了速度−时间图像的“拟合”方法,强调平滑曲线比折线会与实际情况更接近。
教师在此处应注意,如果打点计时器打出的纸带是用手拉着运动的,绘制出的 v−t 图像往往没有规律。
3.“练习与应用”参考答案与提示
本节共 3 道习题,练习在不同情境中理解平均速度和瞬时速度的关系。第 1 题判断纸带的运动方向并用近似方法计算瞬时速度。第 2 题根据 v-t图像分析物体的运动情境。第 3 题计算汽车刹车过程中某段时间的平均速度。分别从实验、图像和联系实际三个维度设置练习,帮助学生正确理解速度的相关概念。
1.(1)因相等时间间隔内重物下落的位移越来越大,故纸带左端与重物相连。
(2)可以测出 A 点与其右方相邻一点间的距离,记为 Δx = 7.0×10-3 m,对应时间为 Δt = 0.02 s,则这两点间的平均速度 v = \(\frac{{\Delta x}}{{\Delta t}}\) = 0.35 m/s。
因为在要求不高的情况下,可以认为 Δt = 0.02 s 是很小的,所以可以认为 A 点的速度 vA = 0.35 m/s。
提示:用 v = \(\frac{{\Delta x}}{{\Delta t}}\) 计算平均速度,当 Δt 非常非常小时,v = vA。但在实际测量中要根据需要及所用刻度尺的情况,在要测量的 A 点附近选取合适的位移和时间。
2.(1)甲具有一定的初速度,乙的初速度为 0。
(2)甲的速度不变,乙先做加速运动,再做匀速运动,最后做减速运动。
(3)甲、乙的运动方向都不发生变化。
3.(1)前 1 s 的平均速度;略小些;(2)2 m/s
提示:(1)汽车全程的平均速度大小是 v = \(\frac{{{s_1} + {s_2} + {s_3} + {s_4} + {s_5}}}{t}\) = \(\frac{{9{\rm{m}} + 7{\rm{m}} + 5{\rm{m}} + 3{\rm{m}} + 1{\rm{m}}}}{{5{\rm{s}}}}\) = 5 m/s。
同理,求得汽车前1 s的平均速度大小是 v1 = 9 m/s,前 2 s 的平均速度大小是 v2 = 8 m/s;前 3 s 的平均速度大小是 v3 = 7 m/s,前 4 s 的平均速度大小是 v4 = 6 m/s。
v1 最接近汽车刚制动时的速度,它比汽车刚制动时的速度略小些。
(2)v = \(\frac{{{s_4} + {s_5}}}{t}\) = \(\frac{{3{\rm{m}} + 1{\rm{m}}}}{{{\rm{2s}}}}\) = 2 m/s。
发布时间:2020/7/23 下午9:56:13 阅读次数:9216
