第十二章 3 实验:电池电动势和内阻的测量
电动势和内阻都是电源的重要参数。根据闭合电路欧姆定律,有多种方法可以测定电池的电动势和内阻。请你思考并提出一两种实验设计方案。
如图 12.3–1,根据闭合电路的欧姆定律,电源电动势 E、内阻 r,与路端电压 U、电流 I 的关系可以写成
\[E = U + Ir\tag{1}\]如果能测出 U、I 的两组数据,就可以列出两个关于 E、r 的方程,从中解出 E 和 r。因此,用电压表、电流表加上一个滑动变阻器 R,就能测定电源的电动势 E 和内阻 r。这是测量电动势和内阻的一种方法。
如果只有一个电流表没有电压表,你能设计出测量电源电动势和内阻的电路吗?还需要什么器材?如果只有一个电压表呢?
实验中需要测量路端电压 U 和电流 I 两个物理量。然而,是否只需测量两组 U、I 数据,联立方程解得 E 和 r 就行呢?
只测量两组数据,通过联立方程解得 E 和 r,看起来比较简单,误差却可能较大。只有多次测量,并对数据进行处理,才能减小误差。所以,应该使用滑动变阻器改变外电路的电阻,进行多次测量。
为了减小误差,根据多次测量的结果,分别列出若干组联立方程,求出若干组 E 和 r,最后以 E 的平均值和 r 的平均值作为实验结果。这种方法的实验结果比只用两组 U、
采用其他方法也应该进行多次测量。
I 数据求得的结果误差小。
采用另外一种方法,也能减小误差,而且更简便、直观。(1)式可以改写成
U = − Ir + E
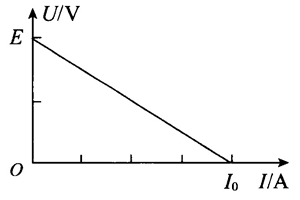
以 U 为纵坐标、I 为横坐标建立平面直角坐标系。根据几组 U、I 的测量数据,在坐标系中描点。某次实验的测量结果如图 12.3–2 所示,此时可以看到这些点大致呈直线分布,画出这条直线。
这条直线与电压及电流坐标轴交点的物理意义是什么?怎样用这些数据得到电源电动势和内阻?
仔细观察你会发现,图 12.3–2中测量数据集中在 U–I 图像的很小区域,这样不利于减小误差。如何调整坐标轴解决这个问题?调整后的直线与坐标轴的交点是否发生改变?
这条直线与 U 坐标轴的交点值表示断路时的路端电压,这时的电压 U 等于电源的电动势 E。根据这条直线可以推出 U = 0 时的短路电流。根据短路电流 I短 与电源内阻 r、电动势 E 的关系
\[r = \frac{E}{{{I_短}}}\]
可以求出电源的内阻 r。
另外,如果从直线方程 U = − Ir + E 的角度理解,通过求解 U–I 图像斜率的绝对值也可以求出电源的内阻 r,即
\[r = \left| {\frac{{\Delta U}}{{\Delta I}}} \right|\]
参考案例 1
测量干电池的电动势和内阻
如图 12.3–1,把滑动变阻器的阻值调到某一较大的数值,分别测出电路中的电压和电流,并记录在预先绘制的表格中。不断减小电阻,得到多组电压 U 和电流 I。作出 U–I 图像,求得干电池的电动势 E 和内阻 r。
由于干电池的内阻较小,当电流 I 变化时,电压 U 的变化可能较小。为了得到更加精确的测量结果,作图时,电压轴的起点标度一般不从 0 开始,应根据实验数据选择合适的起点标度。
旧的干电池的内阻相对于新的干电池要大得多,容易测量。实验中可以选择旧的干电池进行实验。
参考案例 2
测量水果电池的电动势和内阻
把铜片和锌片相隔约 1 cm 插入一个梨中,就制成一个水果电池(图 12.3–3 甲)。铜片和锌片相距越近、插入越深,电池的内阻就越小。铜片是电池的正极,锌片是负极。
把水果电池、电阻箱、电压表等按图 12.3–3 乙连接起来。。根据 E = U + Ir 可以写成
\[E = U + \frac{U}{R}r\]用电压表和电阻箱测出多组电压 U 和电阻 R,并记录在预先绘制的表格中。求出水果电池的电动势和内阻。
水果电池的内阻较大,容易测量。但实验时,内阻会发生明显改变。测量应尽量迅速,在内阻发生较大变化之前结束测量。
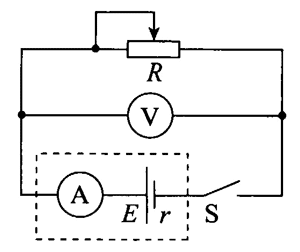
1.某同学按图 12.3–1 的电路测量蓄电池的电动势和内阻。他调整滑动变阻器共测得 5 组电流和电压的数据,如表 1。请作出蓄电池路端电压 U 随电流 I 变化的 U–I 图像,根据 U–I 图像得出蓄电池的电动势和内阻的测量值。
| 电流 I/A | 1.72 | 1.35 | 0.98 | 0.63 | 0.34 |
| 电压 U/V | 1.88 | 1.92 | 1.93 | 1.98 | 1.99 |
2.某同学按图 12.3–1 的电路测定电池组的电动势和内阻。图 12.3–4 已将实验器材进行了部分连接。
(1)请根据实验原理,将图中的实物电路补充完整。
(2)实验时发现电流表坏了,于是移去电流表,同时用电阻箱替换滑动变阻器。重新连接电路,仍然通过 U–I 图像处理实验数据,获得所测电动势和内阻的值。请画出相应的电路图,并说明怎样得到 U–I 图像中电流 I 的数据。
3.某中学生课外科技活动小组利用铜片、锌片和家乡盛产的橙子制作了橙汁电池,他们用如图 12.3–5 所示的实验电路测量这种电池的电动势 E 和内阻 r。
电流表的内阻为 100 Ω,量程为 0 ~ 300 µA;电阻箱阻值的变化范围为 0 ~ 9 999 Ω。
连接电路后,调节电阻箱 R 的阻值,得到的测量数据如表 2 所示。
| R/kΩ | 9 | 8 | 7 | 6 | 5 | 4 | 3 |
| I/µA | 92 | 102 | 115 | 131 | 152 | 180 | 220 |
请作出本实验的 U–I 图像(U 为电阻箱两端的电压,I 为通过电阻箱的电流),根据 U–I 图像得出该橙汁电池的电动势和内阻。
教学分析和教学建议
1.教学目标
(1)经历实验设计过程,理解测定电源电动势和内阻的实验原理。
(2)在理解实验原理的基础上,能完成测电源电动势和内阻的规范实验操作。
(3)学会利用U-I图像处理数据并得出电源的电动势和内阻,进一步体会利用图像进行数据处理的方法。
(4)尝试分析电源电动势和内阻的测量误差,了解实验中减小误差的方法。
2.教材分析与教学建议
本实验是根据闭合电路欧姆定律来测量电源的电动势和内阻,通过动脑、动手、合作、分享,学生既可以深化对电动势和闭合电路欧姆定律的理解,还可以进一步熟悉用图像处理数据的方法、提高操作技能,从而培养学生的科学探究能力和科学态度。
教科书提供了几种实验思路,就其中一种方法进行详细分析,从减小偶然误差的角度出发,提出解方程和图像法两种数据处理方法。最后给出测量干电池和水果电池的电动势和内阻两个参考案例。
本节的教学重点和难点是用 U–I 图像测定电池的电动势和内阻。学生理解了图像的斜率以及与 U 轴、I 轴交点的物理意义,就真正理解了本实验的原理。合理划分刻度、标定U轴的起点坐标,使图像的分布合理、倾斜程度合适,是一项重要的实验技能。
(1)实验思路
教学中可以对教科书提供的实验方法进行详细分析,厘清电动势和内阻测量的思维线索,写出表达式,设计电路图。
教学片段
测定电池电动势和内阻的实验原理
提出问题:电源电动势和内阻不便直接测量,但电源接在电路中,路端电压和电流与电动势和内阻可以通过闭合电路欧姆定律建立联系。请你根据图12-7所示的电路,设计实验方案测定电源的电动势和内阻。要求写出所需测量的物理量,以及电源的电动势和内阻的表达式。
分析:电源电动势 E、内阻 r 与路端电压 U、电流I的关系可以写成 E = U + Ir。如果能测出 U、I 的两组数据,就可以列出两个关于 E、r 的方程,这样就能够从中解出 E 和 r。
改变外电阻 R,读出电压表和电流表的两组数据 U1、I1 和 U2、I2,联立方程组,解得
\[\begin{array}{l}E = \frac{{{I_1}{U_2} - {I_2}{U_1}}}{{{I_1} - {I_2}}}\\r = \frac{{{U_2} - {U_1}}}{{{I_1} - {I_2}}}\end{array}\]
归纳:闭合电路中,有五个重要的物理量:电源电动势E、内阻r、路端电压U、电流I和外电阻R。要求电动势和内阻两个未知量,需要在路端电压 U、电流 I 和外电阻 R 中任选两个物理量,测出两组数据,联立方程组求解即可。
提出问题:请你设计其他方案测定电源的电动势和内阻。要求设计电路图,写出实验器材、所需测量的物理量,以及电源的电动势和内阻的表达式。
分析:闭合电路欧姆定律还可以写成 E = IR + Ir。如果能得到 I、R 的两组数据,就可以得到关于 E 和 r 的两个方程,从中解出 E 和 r。这样,用电流表、电阻箱也可以测定电源的电动势和内阻,实验电路如图 12–8 所示。
闭合电路欧姆定律还可以写成 E = U + \(\frac{U}{R}\)r。如果能得到 U、R 的两组数据,同样能通过解方程组求出 E 和 r。这样,还可以用电压表、电阻箱来测定电源的电动势和内阻,实验电路如图 12–9 所示。
学生通过利用闭合电路欧姆定律公式变形来设计测量电源电动势和内阻的实验方案,既提高了实验探究能力,也培养了逻辑思维能力。
(2)数据分析
教科书先从学生已有的认知水平出发,提出一种数据处理的方案:实际操作中为了减小偶然误差,需要测量多次,求出若干组 E 和 r,最后以 E 的平均值和 r 的平均值作为实验结果。然后详细介绍了用图像处理数据的方法。教学中要让学生理解图像方法的优点,结合上节已经学过的电源 U–I 图像的物理意义,从图像得到电池电动势和内阻的值。学生常常出现的问题有:不理解用囹像法处理数据同样可以减小实验的偶然误差;不会根据图像的物理意义来求 E 和 r,有的从图像上取两点的坐标值列方程组求解 E 和 r。
教学片段
利用 U–I 图像测定电池电动势和内阻
提出问题:如图 12–7 所示,当改变外电阻 R 时,电流表示数 I 和电压表示数 U 同时变化,请你大致画出 U–I 图像,利用数学知识、结合物理规律分析图像的纵、横截距和斜率的物理意义。
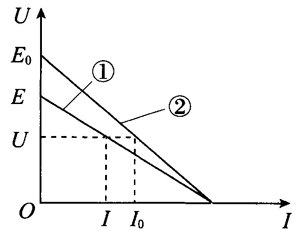
分析:闭合电路欧姆定律可以写成 U = − Ir + E。对于电池来说,电动势 E 和内阻 r 可以看作不变,所以路端电压 U 是电流I的一次函数,U–I 图像是一条斜向下的直线,如图 12–10 所示。
图像在 U 轴上的截距是电流 I 为 0 时(外电阻 R 极大或断路)路端电压的值,等于电源的电动势 E。图像在雎由上的截距是路端电压为 0 时(外电阻 R 极小或短路)的电流(即短路电流)I0。电池内阻 r = \(\frac{E}{{{I_0}}}\),即图像斜率的绝对值。
作 U–I 图像:把可变电阻R的阻值调到某一较大的数值,分别测出电压和电流值,并记录在学生预先设计的表格中。不断减小电阻,得到多组电压、电流值。根据所测数据,适当标定刻度。如果 U 轴从 0 开始划分刻度,作出的图像往往倾斜程度很小,且分布在坐标纸的上半部分,会造成较大妁测量误差。为此,可以选择稍小于路端电压U的测量值的某一数值作为 U 轴的起点坐标。注意此时图像与,轴的交点不再是短路电流 I0,可以从图像上选择两点求斜率得到内阻 r。
在画图像时,要指导学生尽量使数据点均匀分布在直线两侧,个别偏离直线太远的点可以舍弃。并让学生理解这样做可以减小偶然误差,提高测量精度。
提出问题:电源开路时,正、负极间的电压等于电动势E。若测得电源短路时的电流 I0,根据电源内阻 r = \(\frac{E}{{{I_0}}}\),能否用电压表和电流表直接测量得到电池的电动势 E 和内阻 r 呢?
分析:中学物理实验室学生实验用到的电压表不能看作理想电压表,用电压表直接测电源两端的电压,此时电路中有微小电流,结果会稍小于电源电动势;而直接用电流表测电源的短路电流,会超过量程损毁电流表。
目前广泛使用的数字万用表,电压挡内阻可达 10 MΩ,可以看作理想电压表,用电压挡直接测量电池两极间的电压就可以认为等于电源电动势;电流挡的量程可以达到 20 A,可以直接连在电池两端测量短路电流(操作一定要迅速),从而方便得出电源内阻。
要让学生从实验原理出发,在实际操作中积极思考,学会坐标变换的方法,熟悉划分坐标轴刻度、描点画线的实验技能,提高科学探究能力。
(3)系统误差分析
上面提到的数据处理方法可以减小偶然误差。由于电压表、电流表酌内阻对实验电路的影响,本实验还存在系统误差。对有余力的学生,可以引导他们深入思考,促进对物理规律的深层理解和灵活应用。
①图 12–7 中电压表示数等于路端电压,电流表示数小于通过电源的电流从而产生系统误差。
根据闭合电路欧姆定律,两次测量的方程为
\[\begin{array}{l}{E_测} = {U_1} + {I_1}{r_测}\\{E_测} = {U_2} + {I_2}{r_测}\end{array}\]
解得
\[\begin{array}{l}{r_测} = \frac{{{U_2} - {U_1}}}{{{I_1} - {I_2}}}\\{E_测} = \frac{{{I_1}{U_2} - {I_2}{U_1}}}{{{I_1} - {I_2}}}\end{array}\]
设电源电动势和内阻的真实值分别为 E0、r0,若考虑电压表内阻,方程组为
\[\begin{array}{l}{E_0} = {U_1} + ({I_1} + \frac{{{U_1}}}{{{R_V}}}){r_0}\\{E_0} = {U_2} + ({I_2} + \frac{{{U_2}}}{{{R_V}}}){r_0}\end{array}\]
解得
\[\begin{array}{l}{r_0} = \frac{{{U_2} - {U_1}}}{{({I_1} - {I_2}) - \frac{{{U_2} - {U_1}}}{{{R_V}}}}}\\{E_0} = \frac{{{I_1}{U_2} - {I_2}{U_1}}}{{({I_1} - {I_2}) - \frac{{{U_2} - {U_1}}}{{{R_V}}}}}\end{array}\]
比较得 E0 > E测,r0 > r测。
以上是定量计算分析,还可以利用电源的 U–I 图像来定性分析。
如图 12–11 所示,直线①是根据 U、I 的测量值作出的 U–I 图像。通过电源的电流为 I0,由于 I < I0 = I + \(\frac{U}{{{R_V}}}\),而且 U 越大,I 和 I0 之间的的差距就越大,而电压表的示数 U 就是路端电压的真实值 U0,除了读数会有偶然误差外,可以认为 U = U0。经过修正后,直线②就是电源真实值反映的 U–I 图像。由图像可以很直观地看出 E < E0,r < r0。
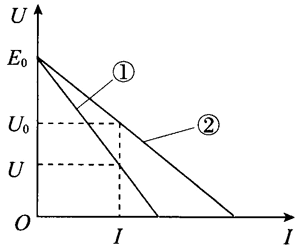
②图 12–12 中电流表示数等于通过电源的电流,电压表示数小于路端电压从而产生系统误差。
若考虑电流表内阻,应用闭合电路欧姆定律,方程组为
\[\begin{array}{l}{E_0} = {U_1} + {I_1}({r_0} + {R_A})\\{E_0} = {U_2} + {I_2}({r_0} + {R_A})\end{array}\]
解得
\[\begin{array}{l}{r_0} = \frac{{{U_2} - {U_1}}}{{({I_1} - {I_2})}} - {R_A}\\{E_0} = \frac{{{I_1}{U_2} - {I_2}{U_1}}}{{{I_1} - {I_2}}}\end{array}\]
比较得 E0 = E测,r0 < r测。
以上是定量计算分析,也可以利用电源的 U–I 图像来定性分析。
如图 12–13 所示,直线①是根据 U、I 的测量值作出的 U–I 图像,路端电压为 U0。由于 U < U0 = U + IRA,而且 I 越大,U 和 U0 之间的误差就越大,而电流表的示数,就是流过电源的电流的真实值 I0,除了读数会有偶然误差外,可以认为 I = I0。经过修正后,直线②就是电源真实值反映的 U–I 图像。由图像可以很直观地看出 E = E0,r > r0。
由以上分析可以看出,r测 = r0 + RA,把电流表和电源等效为一个新电源,如图 12–14 虚线框所示。这个等效电源的内阻 r 为 r0 和 RA 的串联总电阻,也就是内阻的测量值。
由以上分析还可以知道,要减小测量电源内阻的系统误差,电流表的内阻必须很小,使得 r0 远大于 RA。这个要求在实验室测定干电池的内阻时很难满足,所以测量干电池的电动势和内阻常常用图 12–7。而水果电池的内阻可以达到几千欧,满足 r0 远大于 RA 这个条件,所以测量水果电池的电动势和内阻常常用图 12–12。
3.“练习与应用”参考答案与提示
第1题要求应用图像来处理实验数据,涉及对 U–I 图像的物理意义的认识,以及描绘 U–I 图像的基本技能。第2题要求在明确实验原理、画出电路图的基础上进行实物连线,并且能够对实验方案进行合理的修改以顺利完成实验,对科学探究能力要求较高。第3题是一个测水果(橙子)电池电动势和内阻的实验实例,要求在明确实验目的、理解实验方案的基础上,根据实验数据作出正确的U-I图像,并利用图像得出实验结论。
1.U–I 图像如图 12–15 所示,E = 2.03 V,r = 0.08 Ω
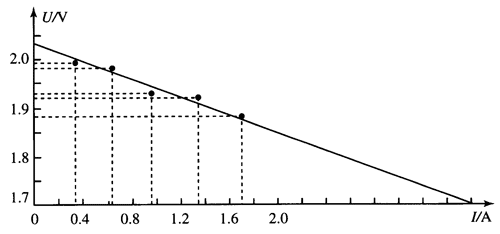
2.(1)实物电路的连线补充如图 12–16 所示。
(2)电路如图 12–17 所示。电压表的读数为 U,电阻箱的读数为 R,则干路电流 I = \(\frac{U}{R}\),多测量几组数据,仍然可通过 U–I 图像完成实验数据的处理。
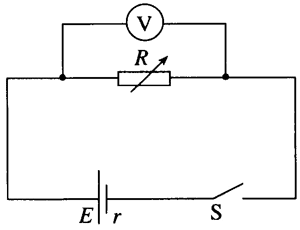
3.U–I 图像如图 12–18 所示,E = 0.95 V,r = 1.2 kΩ
提示:依题意,设电流表的内阻为 rg,则此闭合电路的路端电压 U = I(R + rg)。
代入数据,重新计算数据填入下表。
|
R/kΩ |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
|
I/μA |
92 |
102 |
115 |
131 |
152 |
180 |
220 |
|
U/V |
0.837 |
0.826 |
0.817 |
0.799 |
0.775 |
0.738 |
0.682 |
以 U 为纵坐标,I 为横坐标建立平面直角坐标系,取合适的标度,用 U 与 I 的数值描点、拟合出一条直线,作出 U–I 图像如图 12–18 所示。图像中纵轴上的截距为橙汁电池的电动势 E,图像斜率的绝对值即为橙汁电池的内阻 r。
可得橙汁电池的电动势 E = 0.95 V,内阻 r = 1.2 kΩ。
发布时间:2020/7/14 上午9:31:50 阅读次数:15203
