走进物理课堂之前
赵凯华[1]
一群顽童,衣着五色斑斓,凑在一起,专爱找些新鲜游戏来玩。他们上树掏鸟蛋、下河捞鱼虾;把蝌蚪养在玻璃罐里,要看它们怎样变青蛙;把鸟蛋放在被窝里孵化,想看小鸟怎样从壳里往外爬,睡觉时把鸟蛋压碎了,弄得被窝一塌糊涂,挨了妈妈的骂。
一天在树下玩耍,一只熟透了的苹果掉下来,他们就辩论起来。
苹果是不是越落越快?不过他们很快就达成一致:是的,苹果越落越快。
怎见得?苹果刚离开树枝时几乎是静止的,落地前已相当快,于是就摔烂了。
文静的紫珠说:“只说苹果越落越快,没什么了不起,谁能说出苹果下落怎么个越来越快法?”
黑柱说:“苹果越落越快,就是它的速度正比于落下的距离呗!比如它落下2 m时的速度是落下1 m时速度的两倍。”
白胖说:“我看是苹果的速度正比于落下的时间,它下落2 s后的速度是下落1 s后速度的两倍。”
红孩思考了一会儿说:“你们都说速度的变化,可是速度很难测量,还不如说落下的距离。我猜,要是苹果在第1 s内下落的距离是1,那么,在第2 s内下落的距离就是2,在第3 s内下落的距离就是3,等等。我这个想法容易用实验来检验。”孩子们七嘴八舌,莫衷一是。
坐在一边的蓝仔插进来说:“实验是必须做的,不过垂直下落太快,也许得利用斜面。我得回去好好想想,要讲清道理。”天色已晚,黄娃建议明天到游戏场去做实验,于是大家就散伙回家了。

第二天大家来到游戏场,蓝仔宣布,他对红孩的猜测有修正,每秒落下的距离不是
1 ∶ 2 ∶ 3 ∶ 4 ∶ 5 ∶ …
1 ∶ 3 ∶ 5 ∶ 7 ∶ 9 ∶ …
白胖说:怪了!凭什么不是下面这样的?
2 ∶ 4 ∶ 6 ∶ 8 ∶ 10 ∶ …
黄娃兴冲冲地跑到滑梯上把自己的书包放到斜面上让它下滑,没想到摩擦力太大,书包滑到半路不走了。
黑柱掏出一个皮球,说:“来,用这个!”
大家选红孩当指挥,他要其他人手里各拿一段粉笔头,沿滑梯一字排开。红孩在滑梯顶上,看着手表说:“我喊‘开始!’,就把皮球放开;喊‘1 s’,站在滑梯旁的第一个人用粉笔在球经过的地方画一道;喊‘2 s’,第二个人用粉笔再在球经过的地方画一道;如此等等。”他发号施令,球沿滑梯滚下来。没想到,第一个人画了粉笔道后,没等第二个人画,球已经滚出了滑道。再试,还是那样。大家有点儿懊恼了。
紫珠提议:“我们找物理老师去!”
老师听了他们的汇报后,笑眯眯地说,我带你们到实验室看一样东西。在实验室里看到有盏灯一闪一闪地照着一个下落的球,那球的影像断断续续地,像一串断了线的珍珠,上密下疏。
老师解释说:“这架仪器叫作‘频闪仪’,它每隔一定时间间隔发出一次闪光,于是我们就看到了从静止下落的球每隔一定时间间隔的位置。这个过程用肉眼看还是太快,无法看清楚,更无法测量。我们用照相机连续曝光,把整个过程拍下来。我这里正好有一张拍好的照片,你们可以拿去研究。”
孩子们非常兴奋。
红孩说:“我们先找一张比照片还大些的白纸,以照片上头两个球的影像之间的距离为间隔,精确地在纸上画许多水平线,然后把照片叠放上去,确定以下各个影像的位置,并算出它们之间距离的比例。”
孩子们做得非常认真,水平线画得很平行,间隔也很准确。图画好了,白胖建议先不把照片叠上去,让红孩和蓝仔分别按他们的预期,在落体的频闪照片左右标出球各次将要到达的位置,最后比一比,看看谁对。
|
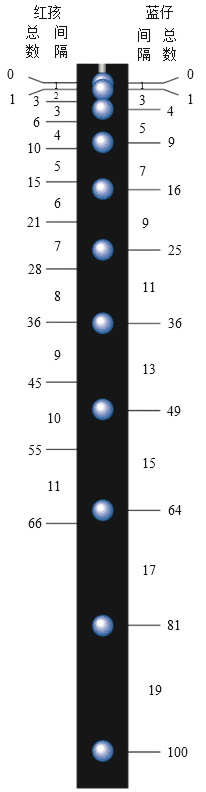
红孩在左边标的是 |
蓝仔在右边标的是 |
|
0 1 1 + 2 = 3 3 + 3 = 6 6 + 4 = 10 10 + 5 = 15 15 + 6 = 21 21 + 7 = 28 28 + 8 = 36 36 + 9 = 45 45 + 10 = 55 |
0 1 1 + 3 = 4 4 + 5 = 9 9 + 7 = 16 16 + 9 = 25 25 + 11 = 36 36 + 13 = 49 49 + 15 = 64 64 + 17 = 81 81 + 19 = 100 |
白胖惊讶地对蓝仔喊道:“没想到你这里都是整数的平方,妙极了!”
于是,大家郑重地把照片叠上去,将起始点对准纸上的零刻度线。
啊!答案出来了,红孩的估计比实际慢了很多,蓝仔的猜测非常符合照片上显示的实际情况。大家为蓝仔欢呼。这时绿妹却质问蓝仔说:“你得给我们说清楚,你是怎么想的。”蓝仔说:“说来话长,得找个有黑板的地方讲。”
孩子们来到教室,把老师也请来了,听蓝仔讲。
蓝仔说:“其实我是吸取了白胖的想法,速度正比于走过的时间。”
设第1 s末的速度为v,初速度为0,所以平均速度为
\(\bar v = \frac{{0 + v}}{2} = \frac{v}{2}\),走过的距离为\(\frac{v}{2}\)× 1 s。
第2 s末的速度为2v,初速度为v,所以平均速度为
\(\bar v = \frac{{v + 2v}}{2} = \frac{{3v}}{2}\),走过的距离为 \(\frac{{3v}}{2}\)× 1 s。
第3 s末的速度为3v,初速度为2v,所以平均速度为
\(\bar v = \frac{{2v + 3v}}{2} = \frac{{5v}}{2}\),走过的距离为 \(\frac{{5v}}{2}\)× 1 s。
依此类推。为了取整数,可令v = 2,于是球在相继各秒下落距离之比就是
1 ∶ 3 ∶ 5 ∶ 7 ∶ 9 ∶ …
如果从零刻度线起算各秒末的总路程,那就是整数的平方
1 ∶ 4 ∶ 9 ∶ 16 ∶ 25 ∶ …
蓝仔讲完后,白胖颇有感慨地说:“真没想到,蓝仔的说法听起来和我的猜测是那样的不同,居然是一致的!可是他把我的想法发挥到了更精致的程度。”
孩子们兴奋之余,没忘了请老师讲话。
老师说:“同学们,你们干了伟大的事。虽然你们得到的结论早已写在物理教科书里,但你们干的,是四个世纪前伟人们干的事。15 世纪欧洲文艺复兴时期,有多位大师参与了落体定律的创立。艺术巨匠达·芬奇提出的落体定律就是红孩的1 ∶ 2 ∶ 3 ∶ 4 ∶ 5 ∶…律,物理学的创立人之一的伽利略提出的落体定律就是蓝仔的1 ∶ 3 ∶ 5 ∶ 7 ∶ 9 ∶…律,最后是伽利略自己用精巧的斜面验证了它,建立了不朽的落体定律,至今每个中学生都在学习它。你们还没有学习这个物理规律就自己找到了它,多么了不起!”
绿妹插嘴道:“达·芬奇的名画我见过一张,叫《蒙娜丽莎》,是在我哥哥带回家来的一本世界名画集中看到的,我哥哥在美术学院学习。”
老师补充说:“挂在蒙娜丽莎嘴角上那一丝‘神秘的微笑’令世人倾倒。应当指出,达·芬奇不仅是艺术家,他还是一位工程师和科学家哩。他设计了多种机器、武器和建筑,搞过人体解剖。科学和艺术是相通的嘛。”
“分析起来你们的研究还真有点儿符合物理学的科学方法哩。”老师继续说:“物理学是探索自然界最基本、最普遍规律的科学,物理学的一般探索过程是通过观察和实验积累经验,在经验事实的基础上建立物理模型,提出(往往是猜测出)简洁的物理规律(物理学要求这些规律是定量化的,也就是用公式或数字表达的),用它们去预言未知现象,再用新的实验去检验这些物理模型和物理规律,去否定或进一步修正它们。”
黄娃插问:“老师,什么是物理模型?”
老师解释道:“实际问题往往是复杂的,其中包含一些非本质的枝节,物理模型就是把实际问题理想化,先略去一些次要因素,突出其主要因素。不这样做我们就得不到简洁的物理规律。拿你们研究的落体规律来说,空气的阻力或斜面的摩擦力就是次要因素,不排除和忽略它们,我们就得不到简洁的落体定律。你黄娃的书包在滑梯上滑不下去,不是再好不过地说明了这个问题吗?”
白胖问:“老师,您说简洁的物理规律是什么意思?”
老师说:“对问题认识得越深刻,得到的规律就显得越简洁。你不觉得蓝仔的整数的平方律1 ∶ 22 ∶ 32 ∶ 42 ∶ 52 ∶…比奇数律1 ∶ 3 ∶ 5 ∶ 7 ∶ 9 ∶…更优美吗?其实还有更简洁的说法。物理学把每秒内速度的增加量叫作‘加速度’,这个概念是伽利略在研究落体定律时创建的。蓝仔的(其实也是你白胖的)落体模型可以概括为‘落体运动是加速度不变的运动’,这不是更简洁吗?物理学中把这种运动叫作‘匀加速运动’,即‘落体运动是匀加速运动’。认识一步一步地深入要靠逻辑推理,要靠数学,数学可以把表面上看起来不同的说法联系在一起,在认识上把它们统一起来。”
黑柱忽然问:“落体就是越落越快呗,研究得那么细有什么用?”
大家面面相觑,都愣住了。
老师从皮包里掏出一张画,上面画的是一个航天员站在月球的表面,双手各丢下一把榔头和一根鹰的羽毛,检验它们在月球上没有空气的条件下是否落得一样快。这位航天员是阿波罗15 号的斯科特,他说,如果没有伽利略落体定律的发现,他就不可能站在那个地方。于是,他情不自禁地在月球上重复他在中学时就在抽空的玻璃管内看到的鸡毛铜钱实验。
老师说:“航天员深刻地知道,虽然仅靠伽利略的落体定律还不能登月,但没有以伽利略落体定律为代表的科学基础,人类社会是不会有今天辉煌的科学技术成就的。物理学是所有现代技术的基础,也是其他自然科学(如化学、生命科学)的基础。同学们今天学习物理学,主要不是马上去用它,而是为将来掌握高科技打好基础。学物理就得从根上学起,从伽利略的加速度概念和落体定律开始。”
孩子们又活跃起来,热切希望跟老师学好物理课。
[1] 赵凯华(1930 — ),北京大学教授,曾任中国物理学会副理事长兼教学委员会主任。
发布时间:2020/7/9 下午8:11:43 阅读次数:3661
