第 2 节  闭合电路的欧姆定律  教学建议

1．教学目标

（1）知道电源是通过非静电力做功将其他形式的能转化为电能的装置，知道电动势的定义式。

（2）经历闭合电路欧姆定律的理论推导过程，理解内、外电路的能量转化，体验能量转化和守恒定律在电路中的具体应用。

（3）理解闭合电路的欧姆定律，通过探究电源两端电压与电流的关系，体会图像法在研究物理问题中的作用。

（4）能根据闭合电路欧姆定律解释路端电压与负载的关系。

（5）知道欧姆表测量电阻的原理。

（6）了解电源短路可能会带来的危害，加强安全用电意识。

2．教材分析与教学建议

本节内容包括电动势概念、闭合电路欧姆定律以及应用该定律分析路端电压与负载的关系。通过本节的学习，学生可以在上一章的基础上对电路的认识更加完整。通过电动势概念的建立和推导闭合电路欧姆定律，为学生深入理解能量守恒定律提供物理事实，在电场和电路情景下培养学生的能量观念。通过应用闭合电路欧姆定律分析路端电压与负载的关系和欧姆表测量电阻的原理的拓展学习，学生应用物理规律进行推理，解决实际问题，促进科学思维的发展。

教科书首先通过节前“问题”引发学生的认知冲突，激发学生从能量转化的角度认识电源，建立电动势的概念；接若应用电动势概念和能量守恒定律推导闭合电路欧姆定律；最后通过应用闭合电路欧姆定律分析路端电压与负载的关系和欧姆表测量电阻的原理来深化对物理规律的认识。以往的教科书把电动势和闭合电路的欧姆定律这两个内容各立一节，独立编排，而且两节之间又穿插了其他内容。现在教科书把这两个内容合为一节，其目的是：在电动势的概念之后立即进行闭合电路欧姆定律的推导，知识的逻辑体系严谨，便于教学。另外，电动势的概念中渗透了“把其他形式的能转化为电势能”，而闭合电路欧姆定律渗透了“把电势能转化为其他形式的能”，使学生对闭合电路的能量转化和守恒有了完整、清晰的认识。

电动势是本节的重要概念，也是本节的难点。这是因为“非静电力”是一个非常抽象的概念。教科书通过对电源内部电场的分析，得出“电源是通过非静电力做功把其他形式的能转化为电势能的装置”，让学生从功和能的角度理解非静电力，知道非静电力在电路中所起的作用，并能从非静电力做功的角度去理解电动势的概念。

闭合电路欧姆定律是本节的重点知识，是分析解决电路问题的基本规律。它是在初中所学部分电路欧姆定律基础上的进一步提升。通过分析闭合电路中电势的升高和降低及其规律，学生可以深化对电场中电势和电势差概念的理解。在过去的教学中，闭合电路的欧姆定律是通过儿童滑梯的比喻引入的。仅从学习这个知识点来说，这样引入比较简单，学生容易接受。但是，闭合电路欧姆定律在体现功能关系问题上是一个很好的素材，它能够充分体现功和能的概念在物理学中的重要性。通过引导学生利用能量守恒定律来推导闭合电路欧姆定律，既巩固深化了电动势的概念，也应用了上一节电功和焦耳定律等知识，使学生对闭合电路中能量的转化与守恒有较为深入的认识。

因此，帮助学生理解电路中的能量转化关系是突破难点、突出重点的关键。应用闭合电路欧姆定律讨论路端电压与负载关系，可以提高学生运用闭合电路欧姆定律分析解决问题的能力。

（1）问题引入

如图 12–2，先用电压表测出电源两端的电压，请学生猜测：

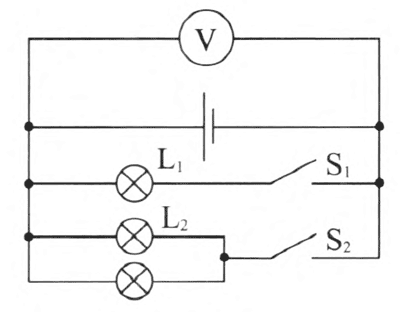
①如果闭合开关 S₁，电压表示数是否变化？

②继续闭合开关 S₂，电压表示数是否变化？灯泡 L₁ 亮度是否变化？

实验时，用插件电路板把电路竖直立起来，能增强可视性。用数字电压表、电源内阻适当大一些，可以增强演示效果。

初中学习的是理想电源，电源两端电压保持不变。所以对于问题①，大部分学生会认为电压表示数不变。实验结果出学生预料，电压表示数明显减小，造成学生的认知冲突，激发学习兴趣。

当闭合开关 S₂，学生根据初中知识“并联电路不会相互影响”认为电压表示数不变，灯泡 L₁ 亮度不变。实验结果又一次出学生预料，电压表示数进一步减小，灯泡 L₁ 亮度明显变暗。这使学生意识到以前学过的知识已经和实验事实相矛盾，对新知识的学习欲望被激发了。

在本节末，可重做达个实验，让学生应用学过的闭合电路欧姆定律、路端电压与负载的关系等知识分析解释观察到的现象。

 

教学片段

问题引入

演示：用电压表测量一节新电池的开路电压，约为 1.5 V。用这节电池给一个规格为“2.2 V  0.3 A”的小灯泡供电，学生观察灯泡亮度。

再拿出一个外形完全相同的电池（提前准备好的旧电池，短路电流小于 100 mA），和刚才的新电池组成电池组，用电压表测量电池组的开路电压，约为 3 V。

设问：用这个电池组给刚才的小灯泡供电，亮度如何变化？

学生大部分会回答“变亮”，演示发现灯泡亮度比刚才暗得多。

这个实验和学生原有认知发生冲突，会大大激发学生探究的欲望。在介绍完电源的内阻这个参量后，可以让学生分析实验现象，比较新、旧电池参数的不同。，

---

教师还可以通过用自制的水果电池演示电源内阻对电路的影响等实验，来激发学生兴趣。

（2）电动势

在第八章“机械能守恒定律”的教学中，学生初步建立了“通过做功研究能量”的思想，此处再次运用这种功能关系的观点来学习电动势。这样既可以使学生对电源电动势的理解深刻，同时也会很好地培养学生的能量观念和模型建构等物理核心素养。如果仅从学习知识的角度看，直接将“电源电动势等于电源没有接入电路耐两极间的电压”告诉学生，会节省很多教学时间，但是学生始终不会对这一概念有较深的理解。

①建构电源模型

首先分析电源的作用：电源之所以能维持外电路中稳定的电流，说明它可以使从外电路流到负极的正电荷经过电源内部又搬回到电源的正极。

然后可以类比水泵的作用，为了维持水的循环流动，水泵克服重力对水做功，把其他形式的能转化为水的重力势能。

接下来引导学生用功和能的观点来分析电源内部。在电源内部的电路里，自由电荷移动的方向与受到的静电力方向相反，移动电荷的不再是静电力，而是“非静电力”。非静电力做功将电荷“移送”到电势能高的电极，增加电势能（消耗其他形式的能）。

所以说，电源是通过非静电力做功，将其他形式的能转化为电能的装置。至于电源内的非静电力是怎样产生的，不必深入介绍。以上过程其实是基于经验事实建构“电源”理想模型的抽象概括过程，有利于培养学生的物理（能量）观念和科学思维。

②电动势定义

不同的抽水机工作时，可以用单位质量的水所增加的重力势能的多少来比较抽水机的抽水能力的差异。

同样道理，可以用把单位电荷量的正电荷从负极搬运到正极，非静电力做功的多少来反映电源的做功本领。物理学中用电动势来表示电源的这一本领。

引导学生根据以上的分析过程给出电动势的定义。掌生类比电场强度和电势的定义，用物理量之比定义出电动势。

 

教学片段

电动势

1．观察实验：用充好电的电容器给小灯泡供电；用手摇发电机给小灯泡供电。

比较两次实验现象，说明发电机和电容器的不同。电容器供电，灯泡闪亮一下，说明灯泡中通过短暂的电流，而手摇发电机可以持续供电，当停止摇动时，灯泡不再发光。

可见，通过转动线圈，可以让电荷在电路内部循环流动。

2．观察实验：带有阀门的连通器两侧水位高度不同，打开阀门，两侧水面很快相平，说明连通器刚才产生了短暂的水流；用水泵把一侧的水举高并搬运到另一侧，在连通器中产生了持续的水流。

分析：水泵克服重力对水做功，把其他形式的能转化为水的重力势能。

类比分析：如教科书图 12.2–2，在电源内部存在着由正极指向负极的电场，静电力阻碍正电荷由负极向正极移动。与水泵类似，电源内部会产生一个与静电力反向的力，推动正电荷不断向正极移动。我们把这个力叫作“非静电力”。

非静电力克服静电力做功，电势能增加。可见电源是通过非静电力做功把其他形式的能转化为电势能的装置。

3．设问：不同的抽水机工作时，可以用单位质量的水所增加的重力势能来反映抽水机的抽水能力的差异。仿照这个想法，你认为应该如何反映电源的做功本领的差异？

组织学生思考、讨论，类比抽水机和电源以及电场强度和电势的定义，得出电源电动势的定义：如果把电荷量为 q 的正电荷在电源内从负极移动到正极，非静电力所做的功为 W，则电源的电动势 E 表示为 E = \(\frac{W}{q}\)。

---

我们常说要让学生经历科学过程，其形式是多种多样的。学生可以通过讨论或实验提出问题，认识新的规律；通过阅读来了解前人的工作过程；在教师的引导下，思路一环套一环地建立新的概念等。这些都是经历科学过程的不同形式。

（3）闭合电路的欧姆定律

教科书的基本思路是从能量的观念（能量守恒定律）分析电路问题：当电路闭合时，非静电力做功把其他形式的能转化为电能（电势能），同时电流做功，把电能转化为内、外电路产生的内能。这样安排教学，注重培养学生用能量观念去分析解决问题，促进学生物理核心素养的形成和发展。

建议教师引导学生分析闭合电路中电源和负载（用电器）的能量转化关系，利用能量守恒定律去建立联系，并利用电动势的定义、电功和焦耳定律进行数学推导，通过演绎推理得出物理结论。通过从定性和定量两个方面进行科学推理、找出规律、形成结论，训练学生正确运用科学思维方法，提升思维品质。

在理论推导出闭合电路欧姆定律后，建议有条件的学校用呵调内阻电池来验证闭合电路中内电压和外电压之和等于电源电动势，即验证闭合电路欧姆定律。由于数字电压表的内阻和准确度远高于指针式电压表，所以这个实验用数字电压表得出的实验数据和理论符合得非常好。理论和实验的完美结合会对学生产生极大的震撼力。从数字电压表读数的正、负，还可以看出在电源内部，由负极到正极电势升高，升高的数值等于电源电动势 E；沿着电流方向电势降落，不但在外电阻上有电势降落 U_外，在内电阻上也有电势降落 U_内，且 E = U_外 + U_内。

教学中还要让学生理解闭合电路欧姆定律两个表达式的物理意义是有区别的。I = \(\frac{E}{R + r}\) 说明 R + r 闭合电路中电流与哪些因素有关，是部分电路欧姆定律的发展，它只适用于外电路电阻是纯电阻的情况。而 E = U_外 + U_内 反映了闭合电路中电势的变化关系，它不但适用于外电路电阻是纯电阻的情况，对外电路含有电动机的电路同样适用。

 

教学片段

非纯电阻元件情况下的闭合电路欧姆定律

若负载是电动机等非纯电阻元件，推导过程如下：

设闭合电路（图 12–3）中的电流为 I，通电时间为 t，则非静电力所做的功

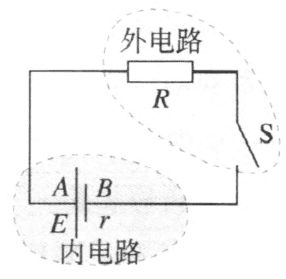
W = EIt

电流通过负载所做的功

W_外 =  U_外It

电流通过内阻 r 产生的内能

Q_内 = I²rt = U_内It

根据能量守恒定律 W = W_外 + Q_内，可得

E = U_外 + U_内

（4）路端电压与负载的关系

教科书首先由闭合电路欧姆定律的表达式变形，得出路端电压随电流变化的关系式，解释了本节“问题”栏目的实验现象。然后思考与讨论两种特殊情况，电源的开路电压和短路电流。这样，学生对电路从一般规律和特殊情况两个方面去分析研究，在掌握知识的同时也体会了物理研究方法。

 

教学片段

路端电压和负载的关系

1．设问：如图 12–4 所示的电路，当开关闭合后，电压表测的是电源电动势吗？

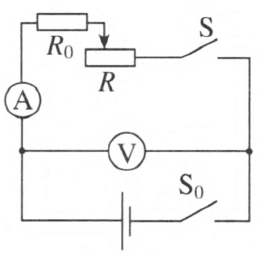
学生不难看出电压表测的是外电压，但仍有人会认为电压表也测出了电源电动势。这时教师可以改变滑动变阻器 R 的阻值，让学生观察电压表的变化。然后指出，电源电动势是反映电源的重要参数，可以看作不变，此时电压表测的不是电动势，而是外电压，也叫路端电压。

2．研究路端电压和电流的关系

改变滑动变阻器 R 的阻值，记录电压表和电流表的读数，重复多次。

用 Excel 画出路端电压和电流的关系图像（图 12–5）。

设问：为什么路端电压和电流满足线性关系？

由闭合电路欧姆定律 E = U_外 + U_内，路端电压 U 实际上就是外电压 U_外，考虑到 U_内 = Ir，可以得出路端电压的表达式 U = E − Ir，表达式中电流 I 是自变量，路端电压 U 是因变量，电源的两个参数电动势 E 和内阻 r 是常量，所以路端电压是电流的一次函数。

分析、思考并回答下面的问题。

（1）分析解释本节“问题”栏目的实验现象。

（2）外电路断开的状态对应于图中的哪个点？这时路端电压与电动势有何关系？

（3）电源短路的状态对应于图中的哪个点？

（4）r 的大小对图像有什么影响？

学生通过思考问题，从图像的纵截距、横截距、斜率分析路端电压、短路电流和内阻，体会用数学方法研究物理问题。

（5）欧姆表的原理

为了不增加学生负担，教科书把这部分内容作为拓展知识。对有余力的学生，通过该内容的学习，既可以深化对闭合电路欧姆定律的理解，又可以体会物理学中常常用到的“转换测量”的思想，提高学生灵活应用知识解决实际问题的能力，有助于培养创新思维和实践意识。

 

教学片段

欧姆表的原理

图 12–6 的电路中，电源的电动势 E = 1.5 V，内阻 r = 0.5 Ω，电流表满偏电流 I_g = 10 mA，电流表的电阻 R_g = 7.5 Ω，A、B为接线柱。

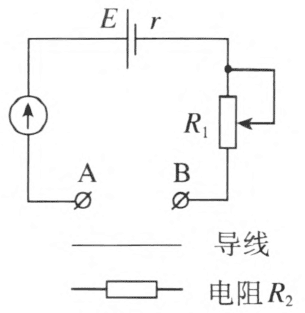
（1）用一条导线把 A、B 直接连起来，此时应把 R₁ 调节为多少，才能使电流表恰好达到满偏电流？

（2）调至满偏后保持 R₁ 不变，在 A、B 间接入一个 150 Ω 的定值电阻 R₂，电流表指针指着多少刻度的位置？

（3）如果把任意电阻 R 接在 A、B 之间，电流表读数 I 与 R 的值有什么关系？

由闭合电路欧姆定律可得：（1）当两个接线柱直接连到一起，且表头指针恰好满偏时，R₁ 的值为 142 Ω。（2）接入定值电阻 R₂ 后，电流表指针指在“5 mA”刻度的位置，即恰好为电流表满刻度的一半。（3）电流表读数 I 与 R 的关系为 R = \(\frac{{1.5{\rm{V}}}}{I}\) − 150 Ω。

以上计算使我们进一步想到，如果把题目中电流表的“10 mA”刻度线标为“0 Ω”，“5 mA”刻度线标为“150 Ω”，其他电流刻度则按 R = \(\frac{{1.5{\rm{V}}}}{I}\) − 150 Ω 的规律换成电阻的标度，它岂不成了可以直接测量电阻的仪表？从 A、B 接线柱引出两支表笔，把表笔接在被测导体的两端（教科书图 12.2–6），从刻度盘上直接读出导体电阻的数值，这不是很方便吗？

教科书图 12.2–6 虚线框中的电路，其实就是一个简单的欧姆表电路。实际的欧姆表就是在这个原理的基础上制作的。

---

这个教学片段先让学生做闭合电路欧姆定律的习题，使学生体会到闭合电路中某一电阻的变化会引起电流的变化，不同的电阻值和电流表的读数具有一一对应关系，从而实现把电流表改装成欧姆表。

3．“练习与应用”参考答案与提示

本节的“练习与应用”主要是应用闭合电路的欧姆定律分析和解决问题。第 1 题涉及非静电力做功快慢，即功率的问题。第 2、3 题联系生活和科技，通过对袖珍手电筒所用干电池和太阳能电池板内阻的推算，进一步巩固对闭合电路欧姆定律的应用和理解。第 4 题通过定量计算，让学生进一步体会路端电压随负载的变化而变化。第 5 题涉及电路设计，是一道综合性题目，对学生灵活处理问题的能力要求较高。第 6 题是一道理论紧密联系实际的题目，应用闭合电路的欧姆定律进行动态分析，解释日常生活中常见的物理现象。第 7 题研究充电宝储存的能量，重在联系实际，培养学生的科学态度与责任。

 

1．乘积 EI 的单位是瓦特。

因为 EI = \(\frac{Eq}{t}\) = \(\frac{W}{t}\) = P，所以 EI 表示非静电力做功的功率，也就是电源将其他形式的能转化为电能的电功率。

 

2．1.6 Ω

提示：每节干电池的电动势为 1.5 V。日常生活中的袖珍手电筒使用两节干电池时，通常为这两节干电池串联，因此电源的电动势为 3.0 V。设每节干电池的内阻为 r，两节干电池串联的总内电源内阻为 2r。由题意得 U_内 = E − U_外 = （3.0 − 2.2）V = 0.8 V。又因为 U_内 = 2rI，所以 r = \(\frac{U_内}{2I}\) = \(\frac{{0.8}}{{2 \times 0.25}}\) Ω = 1.6 Ω。

 

3．16.74 Ω

提示：不接负载时的电压即为电动势，因此 E = 3.85 V，短路时外电路电阻 R = 0。根据闭合电路的欧姆定律得 I = \(\frac{E}{r}\) = \(\frac{3.85}{0.23}\) Ω = 16.74 Ω。

 

 

4．3.72 V：4.3 V

提示：当外电阻为 4.0 Ω 时，电流 I = \(\frac{U_外}{R}\) = 1.0 A。再由闭合电路的欧姆定律 E = I（R + r），可得 r = 0.5 Ω。当在外电路并联一个 6.0 Ω 的电阻时，R_并 = \(\frac{4 \times 6}{4 + 6}\) Ω = 2.4 Ω，电路总电流为 Iʹ = \(\frac{E}{R_并 + r}\) = \(\frac{4.5}{2.4 + 5}\) A = 1.55 A，路端电压为 U_外ʹ = IʹR_并 = 3.72 V。当外电路串联一个 6.0 Ω 的电阻时，R_串 = 10 Ω，电路电流为 Iʺ = \(\frac{E}{R_串 + r}\) = \(\frac{4.5}{10 + 5}\) A = 0.43 A，路端电压为 U_外ʺ = IʺR_串 = 4.3 V。

 

5．5；10 Ω

提示：设至少需要 n 节电池，串联的分压电阻为 R₀。因为路端电压必须大于（或等于）用电器的额定电压，即 nE – Inr ≥ U，得到 n ≥ \(\frac{U}{E - Ir}\) = \(\frac{8}{1.4}\) = 4.3。可见，n 取整数的最小值为 5。这时路端电压 Uʹ = 5E – I×5r = 7 V，需要串联的分压电阻为 R₀ = \(\frac{U^\prime - U}{I}\) = \(\frac{7 - 6}{0.1}\) Ω = 10 Ω。

 

6．将电阻 r 等效入电源的内阻，则在车灯通电且汽车启动前，车灯所用的电压为路端电压。

当汽车启动时，启动开关闭合，电路中的总电阻减小，总电流增大，电源内电压增大，则路端电压减小；车灯所用的电压仍为路端电压，所以它们会变暗。

汽车发动之后，启动开关断开，电动机停止工作，电路中的总电阻增大，总电流减小，电源内电压减小，则路端电压增大到启动前的值，车灯恢复正常亮度。

 

7．充电宝铭牌标注“10 000 mA·h”和“3.7 V”，可得充电宝储存的能量 E = 10 000 mA·h×3.7 V = 37 W·h。由于这个充电宝储存的能量小于规定的 160 W·h，所以可以把它带上飞机。