12

第十二章

电能  能量守恒定律

第十二章  电能  能量守恒定律

课程标准的要求

3.2.4  理解闭合电路欧姆定律。会测量电源的电动势和内阻。

3.2.5  理解电功、电功率及焦耳定律，能用焦耳定律解释生产生活中的电热现象。

3.2.6  能分析和解决家庭电路中的简单问题，能将安全用电和节约用电的知识应用于生活实际。

3.4.1  了解利用水能、风能、太阳能和核能的方式。初步了解核裂变与核聚变。

3.4.2  知道不同形式的能量可互相转化，在转化过程中能量总量保持不变，能量转化是有方向性的。

3.4.3  了解可再生能源和不可再生能源的分类，认识能源的过度开发和利用对环境的影响。

3.4.4  认识环境污染的危害，了解科学·技术·社会·环境协调发展的重要性，具有环境保护的意识和行为。

本章教材概述

教科书根据课程标准的要求及整体安排，将“电路中的能量转化”“闭合电路的欧姆定律”“测电源电动势和内阻”这些电路中与能量相关的内容与“能源与可持续发展”这一主题的内容整合组成本章内容。

按照循序渐进的原则，教科书安排在上一章先学习部分电路规律，在本章再学习闭合电路的相关物理规律。闭合电路欧姆定律是部分电路欧姆定律的延伸，是整个电路部分的中心内容，也是复杂电路分析的基础，在整个电路知识体系中起着承上启下的作用。

能量观念是重要的物理观念，电能是能量观念的重要组成部分，电路中的能量转化既是前一章知识的拓展，又是能量转化与守恒定律的具体案例。学生在本章中将根据静电力做功来建立电功、电能的概念，用能的转化与守恒的观点分析解决闭合电路问题，充分展示功能关系在物理学中的重要性。

学生在《普通高中教科书物理必修第二册》已经学过机械能守恒定律，在初中也学过能量守恒定律，教科书在运用能量守恒观念分析、解决电路问题的基础上，进一步拓展到能量转化的方向性上，并进一步介绍“能量转移或转化的方向性”“能源与环境”“能源与社会发展”及“STSE 汽车和能源”内容，既使学生对能源问题及其解决有了全面的认识，又增强了学生对汽车能源消耗、环境污染和未来汽车发展方向的认识。

在本章编写时，还有以下一些考虑。

1．重视知识的应用

本章共 4 节内容，基本概念和规律并不多，主要是电功、电功率、焦耳定律和能量守恒定律，这些内容在初中也已经涉及。在高中的学习中，着重于这些知识的应用，例如第 1 节“电路中的能量转化”的名称就不同于原教科书的“焦耳定律”。原教科书“焦耳定律”的主要目标是知识的传授，“电路中的能量转化”虽然也有电功、电功率和焦耳定律的知识内容，但强化了对电动机能量转化和功率关系的分析。通过本案例的学习，有利于学生分析空调、电冰箱等家用电器的能量转化。在第 2 节“闭合电路的欧姆定律”中应用能量守恒定律推导了闭合电路的欧姆定律，在第 3 节“实验：电池电动势和内阻的测量”中应用闭合电路的欧姆定律设计实验方案，都是知识的应用。

本章在应用知识解决问题时，体现了科学思维的方法。如在涉及电动机问题时，有如下的“思考与讨论”：“当电动机接上电源后，会带动风扇转动，这里涉及哪些功率？功率间的关系又如何？”通过讨论，学生认识了主要、次要因素，建立了电动机功率间的关系，体现了核心素养中的科学思维要素。

2．强调知识建构的阶段性

物理概念是物理学的基础，搞好物理概念教学是教学成功的基础。由于许多物理概念很抽象，建立过程中的理性思维要求高，导致几个难点概念的教与学比较难处理，其中，电动势概念尤其典型。对抽象概念的教学应遵循物理概念的建构过程，遵循学生的认知发展过程，注重阶段性，需要让学生经历一个从感性到理性，从个别到一般，从现象到本质的渐进过程。例如，对电动势概念的建构至少需要经历三个阶段：一是通过类比，从功能关系和能量转化的角度来理解电动势；二是从全电路的电势升、降角度来理解电动势；三是区分电动势、外电压、内电压。教科书编写“电动势”这一内容时，充分注意到了这种阶段性。

过去是用“电源两极间电压的大小是由电源本身的性质决定的，为了表征电源的这种特性，物理学中引入了电动势的概念”直接引入电动势的概念。本教科书通过对电源内部功能关系的研究，再次强化了“通过做功研究能量”的思想。教科书对电动势这个概念的学习是通过以下几个过程来实现的：①演示，观察、思考电源的作用；②让学生从感性认识逐步深入到理性探究——建立非静电力的概念；③分析不同电源非静电力做功的情况和能量转化情况，为引入做功本领做好铺垫；④比较做功本领，定义电动势；⑤通过测定电动势的实验进一步加强体验。

3．理论探究与实验探究并重

对于“闭合电路的欧姆定律”的探究，考虑到实验探究对器材和实验技能要求较高，以及还有“电池电动势和内阻的测量”实验，教科书仍延续从功能关系的角度分析问题这一思路，采用从能量守恒这一普遍原理进行演绎推导的方式，突出了能量观念的运用。其推导的核心是分析闭合电路以下三部分的能量转化：

外电路  Q_外 = I²Rt

内电路  Q_内 = I²rt

化学反应层  W = Eq =  EIt

要理解前两式，除了需要知道前面学过的焦耳定律外，还必须对内电路和外电路有清晰的认识。因此，教科书在用教科书图 12.2–4 呈现闭合电路的同时，还通过教科书图 12.2–3 指出电源内、外各部分电势高低的情况，阐述电源中及外电路沿电流方向的电势变化。

教科书在“电动势”中用非静电力做功引起的能量转化以及用非静电力做功来定义电动势，这为得到并理解上面第三式打下了基础。在讨论以上三个计算式的关系时，墓于能量转化与守恒的观念，建立闭合电路的欧姆定律就自然“水到渠成”了。

在这之后，依据闭合电路的欧姆定律，进行合理的推理就可以得到“路端电压与负载的关系”以及“断路”和“电源短路”情况下的基本结论。

4．学生实验——统一、基本的要求和灵活、多样的方法相结合

“电池电动势和内阻的测量”是本章的一个重要实验。教科书对这个实验的编写，体现了统一、基本的实验要求和灵活、多样的实验方法相结合的指导思想。

实验原理是基本要求。该实验不管用哪种实验方法和器材，都要根据闭合电路的欧姆定律，测出除电动势、内阻以外的物理量，利用图像或计算，求出电动势和内阻。通过外电路 U、I、R 关系的变换，闭合电路欧姆定律的表达式可以写成多种形式。因此，通过测量 U 和 I，或者 U 和 R，或者 I 和 R 等都可以求得电动势和内阻。实验方法的多样性可以拓展学生的思路，避免死记硬背实验步骤。

数据处理的方法也是基本要求。进行图像分析时，图像中的什么量表示电动势？什么量表示电阻？数据处理时怎样减小偶然误差？这些问题都是基本的问题，因为它们不仅与本实验有关，其他的实验也同样存在类似的问题。因此，这是统一的实验要求，是学生解决实验问题的基本素质。

教科书在编与时拓展了实验方法，使其从特殊向一般转化，有利于学生灵活把握实验原理，也有利于因地制宜地选择实验器材。究竟用哪一种具体的实验方法和器材来测量电源的电动势和内阻，教科书不是提出单一的实验方案，而是给出了两个参考案例，提供了i种电路图供老师和学生根据实际情况选择，体现了对科学探究的注重，渗透了设计性实验的思想，有助于培养学生的创新能力。三种实验方法的实验原理大致相同，但后两种变式涉及“公式变形”“数形结合”等思想，有一定的难度。建议在新课教学时可以就第一种方法进行详细的分析，在综合复习课时，学习多种方法间的联系并学习解决后两种电路所需要的思维方法。

课时安排建议

第 1 节  电路中的能量转化                                               1 课时

第 2 节  闭合电路的欧姆定律                                          1 课时

第 3 节  实验：电池电动势和内阻的测量                      1 课时

第 4 节  能源与可持续发展                                               1 课时

第 1 节  电路中的能量转化  教学建议

1．教学目标

（1）通过实例分析，理解电能转化为其他形式的能是通过电流做功来实现的，加深对功与能量转化关系的认识。

（2）通过推导电功公式和焦耳定律，理解电功、电功率和焦耳定律，能用焦耳定律解释生产、生活中的相关现象。

（3）从能量的转化和守恒角度分析非纯电阻电路中的能量转化，理解电功和电热的区别和联系。

（4）联系生活中的电风扇、空调、电动机等电器设备，体会能量转化与守恒思想，增强理论联系实际的意识。

2．教材分析与教学建议

本节在电场知识和能量守恒定律的基础上学习电功和电功率、焦耳定律，在电场和电路情境下培养学生的能量观念。学生应用物理规律进行推理，加深对概念、规律的理解，促进科学思维的发展。

教科书以节前“问题”引出电功率概念，进而利用电场的知识推导电功的表达式，接着进一步利用能量守恒定律推导焦耳定律。通过对包含电动机的电路中的能量转化的实例分析，加深对电功和电热等概念的理解和辨析。

本节的教学重点是电功概念的建立和理解。这主要因为以下两个方面：一、电流做功的过程就是电能转化为其他形式的能的过程，又一次为学生理解“功是能量转化的量度”提供物理事实；二、用静电力做功的知识推导电功的表达式，使学生对“场”和“路”的联系有了进一步认识。

本节的教学难点是对包含电动机的电路中的能量转化的实例分析。一方面学生需要利用能量转化与守恒的思想建立关系式，学生头脑中必须抽象出清晰的“能流图”；另一方面学生对电功和电热概念容易辨析不清，导致张冠李戴，乱套公式。

因此教师应在教科书内容的基础上，针对重、难点的突破进行教学设计。可以从以下几方面展开教学。

（1）问题引入

教科书以分析电灯、电视、电热水壶、电动汽车等用电器的能量转化问题引入，帮助学生回忆初中所学的能量转化与守恒知识，有利于学生关注能量转化的问题，思维聚焦到本节课内容。

另外，还可以用家庭中电冰箱铭牌引入新课，拓展STSE（科学·技术·社会·环境）教育内容，引导学生关心身边的能源问题。

 

教学片段

问题引入

型号	额定电压                    220 V ~
星级标志                 ****	额定频率                       50 Hz
气候类型             SN·N·ST	输入总功率                     100 W
防触电保护类别                   Ⅰ 类	额定耗电量             0.70 kW·h/24 h
总有效容积                      235 L	噪声（声功率级）           38 dB（A）
冷冻室有效容积                   85 L	冷冻能力                    4.0 kg/24 h
发泡剂                         环戊烷	额定输入电流            0.5 A
重量                            64 kg	制冷剂                     R600a 50 g
灯的最大额定输入功率                                                        15 W

请大家观察电冰箱的铭牌，回答以下问题：

冰箱正常工作时的额定功率是多少？

冰箱正常工作一天大约消耗多少电能？

如果要设计更节能环保的冰箱，可以从哪些方面入手？

---

这样设计，可以引导学生学会阅读家用电器的说明书，利用初中所学的电学知识解决实际问题，培养综合实践能力和节能环保意识。

（2）电功和电功率

教科书通过实例，让学生认识到电能转化为其他形式的能，是通过电流做功来实现的，进一步深化对功是能量转化的量度的认识。接下来指出电流做功的实质是导体中的恒定电场对自由电荷的静电力在做功。本章电路问题中常说的电能，其实质是上一章所学习的电势能。在此基础上，驯导学生由电场的知识推导电功的表达式。

不同的用电器电流做功（消耗电能转化为其他能）的快慢不同，由此引入电功率概念，还可以跟速度等概念进行类比，帮助学生理解。要让学生知道用电器额定功率的含义，并对常见用电器的额定功率有个大致的了解。

（3）焦耳定律

教科书没有通过实验归纳引入焦耳定律，而是从能量守恒定律分析得出的。这里又一次应用了功能关系的思想，培养学生的能量观念。

需要指出的是，在推导焦耳定律的过程中，用到了“Q = W”这个条件，它要求电流做的功“全部变成了热”，即电能全部转化为导体的内能。也就是说，在纯电阻电路的条件下推导出焦耳定律。其实，也可以用焦耳定律处理非纯电阻电路问题。比如，电路中有电动机或者正在充电的电池，那么电能除了转化为内能之外，还转化为机械能或化学能。此时用焦耳定律 Q = I²Rt 计算的只是电能转化为内能的那部分能量，而用电功公式 W =  UIt 计算的是电流所做的总功，也就是电动机或者正在充电的电池消耗的总电能。

（4）电路中的能量转化

教科书从能量转化和守恒的角度分析了包含电动机的电路中的能量转化，为学生深入理解能量守恒定律提供物理事实。教学中可引导学生对能量转化进行讨论，这样有利于学生区分纯电阻电路与非纯电阻电路，辨析公式 W = Ult、Q = I²Rt 不同的物理意义。

由于所学知识的局限，学生对电动机不满足欧姆定律缺乏认识，因此对电功和电热的表达式不能从本质上加以区分。为此，教学中可以设计伏安法实验，让学生从实验现象中认识到电动机不满足欧姆定律。

 

教学片段

电路中的能量转化

提出问题：电流通过用电器的过程中，消耗电能，同时产生其他形式的能，这个能量转化的过程就是电流做功的过程，即电功 W = UIt，而电流通过导体会产生焦耳热 Q = I²Rt。那么，Q 和 W 一定相等吗？

分析：在欧姆定律适用的情况下，电功等于电热，也就是说电流消耗的电能全部转化为内能，所以，欧姆定律适用的电路叫作纯电阻电路，不适用的电路就可以叫作非纯电阻电路。

进行实验：电路图如图 12–1 所示。实验时可以先固定电动机 M，不让它转动，此时消耗的电能全部产生焦耳热，可以用电动机两端的电压 U 和通过电动机的电流 I 来计算电动机的电阻 R。

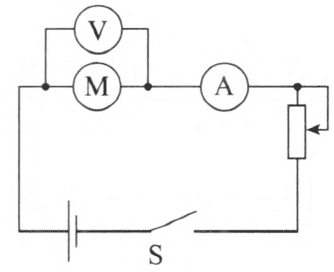
图 12–1

然后放开手，让电动机转动，进行实验，可以看到此时电动机的电然后放开手，让电动机转动，进行实验，可以看到此时电动机的电压、电流、电阻不再满足欧姆定律的关系，即 I < \(\frac{U}{R}\)。

分析论证：由此可见，对于非纯电阻电路，电功 W = UIt，焦耳热 Q = I²Rt，两者并不相等，且 Q < W。即电流通过电动机所做的功只有一部分转化为内能。

进一步引导学生从能量转化与守恒的角度去考虑，如果电路中有电动机，那么电能除了转化为内能之外，还转化为机械能。

让学生根据上述实验测得的两组电压 U 和电流 I 值，计算电动机的热功率与机械功率，以加深学生的理解。

反思：从实验中电动机转动时 U、I、R 三个物理量的数值并不满足欧姆定律的关系式 I = \(\frac{U}{R}\) 的特点出发，再根据对电路能量转化的分析，有关纯电阻电路和非纯电阻电路的区别就比较清楚了。

---

教师要引导学生对上述讨论进行归纳、总结。一方面，总结电功和电热的关系；另一方面，要让学生体会用能量转化和守恒的观点来分析问题的思想方法。

3．“练习与应用”参考答案与提示

本节练习围绕串、并联电路和电路中的能量转化（纯电阻电路）两个内容设计问题。第 1 题要求结合串、并联电路的特点来认识串、并联电路中，各电阻上消耗的电功率与其电阻的关系。这是学习教科书中推导串、并联电路的电阻关系后的一次独立的尝试，对提高学生的逻辑分析能力有较大的帮助。第 2、3、4 题，具体应用电功、电功率的知识，结合欧姆定律和串、并联电路的特点进行定量计算，可以提高学生对电路进行分析和计算的能力。第 4 题与生活实际联系紧密。

 

1．设电阻 R₁ 消耗的电功率为 P₁，电阻 R₂ 消耗的电功率为 P₂，……

（1）串联电路中各处电流相等，设电流为 I，则电功率 P₁ = I²R₁，P₂ = I²R₂，…

P₁∶P₂∶… = R₁∶R₂∶…

此式说明，串联电路中各电阻消耗的电功率与其电阻成正比。

（2）并联电路中各电阻两端的电压相等，设电压为 U，则有 P₁ = \(\frac{U^2}{R_1}\)，P₂ = \(\frac{U^2}{R_2}\)，…

P₁∶P₂∶… = \(\frac{1}{R_1}\)∶\(\frac{1}{R_2}\)∶…

此式说明，并联电路中各电阻消耗的电功率与其电阻的倒数成正比。

 

2．（1）接通开关 S 时，R₁ 被短路，R₂ 直接接在电源两端，电路消耗的电功率为 P₁ = \(\frac{U^2}{R_1}\)。当开关 S 断开时，R₁、R₂ 串联后接到电源上，电路消耗的电功率为 P₂ = \(\frac{U^2}{R_1 + R_2}\)。因为 P₁ > P₂，所以开关 S 接通时，电饭锅处于加热状态；开关 S 断开时，电饭锅处于保温状态。

（2）（\(\sqrt 2 \) − 1）∶1

提示：（2）加热时，P_R2 = \(\frac{U^2}{R_2}\)；保温时，Pʹ_R2 = （\(\frac{U}{R_1 + R_2}\)）²R₂。要使Pʹ_R2 = \(\frac{1}{2}\)P_R2，必有R₁∶R₂ = （\(\sqrt 2 \) − 1）∶1。

 

3．根据电阻的规格可以知道 R_A = R_C < R_B = R_D。电路可以看成是由 R_B、R_C 并联，然后与 R_A、R_D 串联而成。由于电流相同，且并联部分的总电阻小于其中最小的电阻，所以 P_D > P_A >（P_B + P_C）。对于 R_B、R_C 并联部分，由于电压相等，R_C 的电阻小，因此 P_C > P_B。所以 P_D > P_A > P_C > P_B。

 

4．165 V，907.5 W；634.8 W，490.0 W

提示：在用电器只有电热水器 A 时，I = \(\frac{U}{{R_\rm{A}} + 2R}\) = \(\frac{220}{30 + 10}\) A = 5.5 A。电热水器 A 上的电压 U_A = IR_A = 5.5×30 V = 165 V，它消耗的功率 P_A = I²R_A = 5.5²×30 W = 907.5 W。

再并联上电热水壶 B 时，总电流 Iʹ = \(\frac{U}{{\frac{{{R_{\rm{A}}}{R_{\rm{B}}}}}{{{R_{\rm{A}}} + {R_{\rm{B}}}}} + 2R}}\) = \(\frac{{220}}{{\frac{{30 \times 40}}{{30 + 40}} + 10}}\) A = 8.1 A。通过电热水器 A 的电流 I_A = \(\frac{R_\rm{B}}{R_\rm{A} + R_\rm{B}}\)Iʹ = \(\frac{4}{7}\)×8.1 A = 4.6 A，通过电热水壶 B 的电流 I_B = \(\frac{R_\rm{A}}{R_\rm{A} + R_\rm{B}}\)Iʹ = \(\frac{3}{7}\)×8.1 A = 3.5 A。电热水器 A 消耗的功率 P_A = I_A²R_A = 4.6²×30 W = 634.8 W。电热水壶 B 消耗的功率 P_B = I_B²R_B = 3.5²×40 W = 490.0 W。