第 4 节  串联电路和并联电路  教学建议

1．教学目标

（1）分析得出串联和并联电路电流、电压的关系式，并理解其含义，体会严谨的科学推理过程。

（2）依据电流和电压的关系，推导得到串联和并联电路总电阻的表达式，体会等效思想在物理中的运用。

（3）通过建立简化模型，应用串、并联电路规律分析电流表及电压表的改装原理，理解理想电表是一种科学抽象的产物，进一步体会理想化模型的思想方法。

2．教材分析与教学建议

本节的主要内容是：根据恒定电流电路内部电荷稳定分布的特点，分析得出串、并联电路的电流关系式；根据电势及电势差概念，得出串、并联电路的电压关系式；然后由电流及电压关系式出发，结合欧姆定律推导出串、并联电路等效电阻的关系式；最后应用串、并联电路特点分析电流表和电压表的电路结构。

教科书内容的重点是，串、并联电路的总电阻与各部分电阻关系式的含义及电流表、电压表的改装原理。学生学习的难点是，并联电路总电阻随支路电阻变化的关系及电流表、电压表的改装原理。教科书编写的特点是注重讲道理，讲规律的来龙去脉。学生在初中学过串、并联电路的电流、电压、电阻的关系，此处教科书把重点放在讲解这些关系式是怎么得来的，没有直接给出结论，也没有直接应用。电流表及电压表的改装采用先建立电路模型，后应用串、并联电路的知识进行分析的方法。这些都体现了物理学科的科学思维要素．立足于发展学生的思维能力。

（1）问题引入

本节的引课问题是“如果把两个电阻 R₁、R₂ 串联或并联后看成一个电阻，你认为这个电阻跟 R₁、R₂ 应该是怎样的关系？”用这个问题引入是为了引起学生对串、并联电路规律的深入研究。

可能有的学生已经比较熟悉串、并联电阻公式，也可以这样设问：串、并联电阻的总电阻公式是怎么得来的？

还可以将学生思维直接引到电流关系上，提问：串联电路中的电流为什么处处相等？

（2）串、并联电路中的电流和电压

我们知道，初中物理教科书也涉及串联电路和并联电路的电流、电压的关系，那是通过实验总结出来的。这套高中物理教科书以此为基础上了一个台阶：根据电荷守恒的思想，分别得出串联电路和并联电路中各点的电流的关系；又根据各点电势的关系，分别得出两种电路中的电压关系。

教科书这样处理的目的，一方面是从理论分析的角度使学生对串、并联电路中的电流、电压间的关系有更深刻的理解；另一方面是使学生体会到，许多概念、规律都靠逻辑关系联系着，物理学是一个自洽的体系。

这部分物理知识在实际生产、生活中的应用很广，教师可以引导学生讨论见过的电路哪些是串联的，哪些是并联的。比如，家庭电路中的用电器是并联的，节日用的小形灯是串联的，马路上的路灯是并联的，等等。还可以让学生做课题研究，探究楼道里的照明灯电路的电路图，培养学生将物理知识与实际结合的意识和习惯。

（3）串、并联电路中的电阻

教科书首先讲了串联和并联电路的总电阻是等效电阻，两个电阻的效果跟一个电阻产生的效果相同。其次，推导并理解串、并联电路的总电阻与各导体电阻的关系式。

教学中要讲清“等效”的含义是什么。两个电阻可以用一个电阻等效替代，条件是将加在这两个电阻上的电压改加在这一个电阻上，通过干路的电流是一样的。换句话说，对于整个电路来说，如果将这两个电阻去掉，换上这一个电阻，电路中其他部分的电流和电压是一样的，那么这个电阻就可以等效替代那两个电阻。等效思想是物理学中非常重要的思想方法，会给研究问题带来很多方便。高中物理中很多地方用到了等效替代，比如物理量的平均值、有效值，合力和分力等。但是，一定要注意条件。此处教学中强调 U 相同，I 相同，就是引导学生注意等效的条件。

对于串联电路，还可以引导学生讨论串联电路中电压分配跟电阻的关系。比如，站在高压线上的小鸟为什么安然无恙呢？

并联电路中，总电阻随各支路电阻的变化关系是解决实际问题的基础。由于它们之间是倒数关系，比较抽象，建议引导学生具体讨论、归纳。

 

教学片段

并联电路的电阻

问题 1：对比图 11–18 和图 11–19，要用 R 等效替代 R₁ 和 R₂，需要满足什么条件？

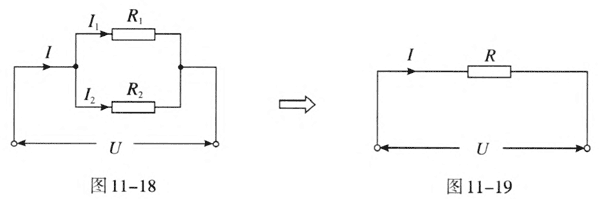
两个电路所加电压相同时，如果干路电流也相同，那么电阻 R 就可等效替代两个并联电阻 R₁ 和 R₂。

问题 2：并联电路的总电阻 R 跟每个支路的电阻 R₁、R₂ 的关系是怎样的？请大家试着推导出来。

问题 3：并联电路中，总电阻比每一支路电阻大还是小？

根据 \(\frac{1}{R}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\) + \(\frac{1}{R_3}\) + … > \(\frac{1}{R_1}\)，可得 R < R₁。

同样可证明 R < R₂，R < R₃ 等。

也就是说，并联电路中总电阻小于任一支路电阻。

形象理解：电阻并联就相当于增大了导体的横截面积，并联的导体越多，横截面积越大，等效电阻就越小。

问题 4：如果并联电路中每个电阻都相同，则总电阻怎样？

若 R₁ = R₂ = R₃ = …，则 \(\frac{1}{R}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\) + \(\frac{1}{R_3}\) + … = \(\frac{n}{R_1}\)，所以 R = \(\frac{R_1}{n}\)。

说明若并联电路中每个电阻都相同，则总电阻等于任一支路电阻的 。

问题 5：若并联电路中有一支路电阻增大，其他电阻不变，那么总电阻怎么变化？

若 R₁ 增大，则 \(\frac{1}{R_1}\) 减小。

由 \(\frac{1}{R}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\) + \(\frac{1}{R_3}\) + … 得 \(\frac{1}{R}\) 减小，R 将增大。

说明并联电路中有一支路电阻增大，其他电阻不变时，总电阻将增大。形象理解：一个支路电阻横截面积变小，总横截面积也变小，等效电阻将增大。

问题 6：若并联支路增多，总电阻怎么变化？

由 \(\frac{1}{R}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\) + \(\frac{1}{R_3}\) + … 得并联电阻越多，说明等号右侧值越大，即 增大，则 R 变小。

形象理解：并联支路增加，相当于增加了横截面积。

问题 7：证明：当一个很大的电阻与一个很小的电阻并联时，总电阻小于很小的电阻，且接近很小的电阻。

若 R₁ ≪ R₂，得 \(\frac{1}{R_1}\) ≫ \(\frac{1}{R_2}\)。

由 \(\frac{1}{R}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\) 知 \(\frac{1}{R}\) 很接近 \(\frac{1}{R_1}\)，则 R 很接近 R₁。

比如 1 Ω 的电阻与 1 000 Ω 的电阻并联，总电阻为 \(\frac{1000}{1001}\) Ω ≈ 1 Ω。

问题 8：电阻 R₁ 和 R₂ 并联，通过两电阻的电流之比为多少？

由于 U₁ = U₂，则 \(\frac{I_1}{I_2}\) = \(\frac{R_2}{R_1}\)。

注意：I₁∶I₂∶I₃ ≠ R₃：R₂：R₁，即如果 R₁：R₂：R₃ = 1：2：3，则电流 I₁∶I₂∶I₃ ≠ 3：2：1！

---

对于并联电路，教师还可以引导学生讨论电流随电阻的分配规律，进而讨论一些实际问题。比如，家庭电路中，用电高峰时灯泡发暗，使用大功率的电炉、电热器时灯泡也发暗，断开后灯泡马上又亮起来，是什么原因？

滑动变阻器在电路中的限流式接法和分压式接法是串、并联电路的重要应用，本节“练习与应用”中第 1 题和第 2 题可做深入分析。

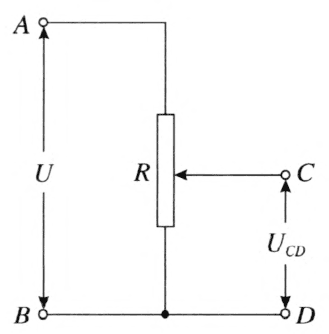
要会判断电路中的总电压和分电压。如图 11–20 电路中 A、B 之间是总电压，C、D 之间是分电压，滑动变阻器 CD 部分的作用是给用电器提供电压。

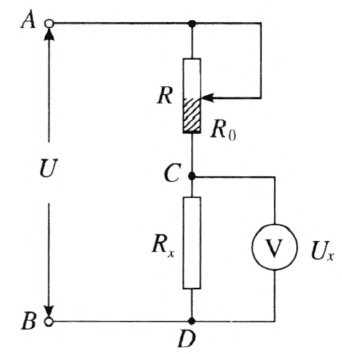
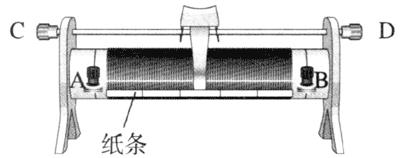
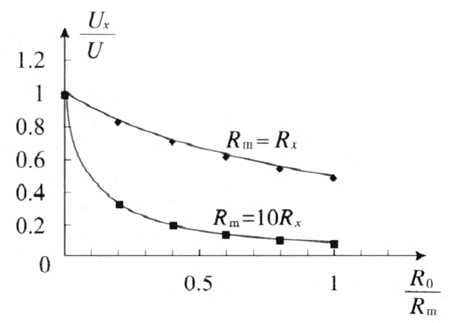
如图 11–21 所示的限流电路，根据串联电路电压的分配规律可推导出电阻 R_x 两端的电压 U_x = \(\frac{{U{R_x}}}{{{R_x} + {R_0}}}\)。高一学生不容易直接看出这个函数的变化关系，建议通过实验引导学生描点绘出 U_x 与 R₀ 间的关系。实验中将滑动变阻器的绕线下端贴上纸条，如图 11–22 所示。在纸条上画一条直线，然后将这条线划分为五等份，每一份对应滑动变阻器总阻值的 \(\frac{1}{5}\)，这样就可以大致知道滑动变阻器接入电路中电阻R₀ 的阻值。按照图 11–21 所示的电路，改变滑片的位置，令 R₀ 分别等于 \(\frac{R_\rm{m}}{5}\)、\(\frac{2R_\rm{m}}{5}\)、\(\frac{3R_\rm{m}}{5}\)、\(\frac{4R_\rm{m}}{5}\)、R_m，R_m 表示滑动变阻器的最大阻值，用电压表测出相应 R_x 两端的电压，在坐标纸上描点作图得出图像。R_x 相同时，滑动变阻器的最大阻值不同，U_x 的变化范围就不同，R_m 越大，U_x 的变化范围越大。如图 11–23 所示分别是滑动变阻器最大阻值 R_m = R_x 和 R_m = 10R_x 的图像。

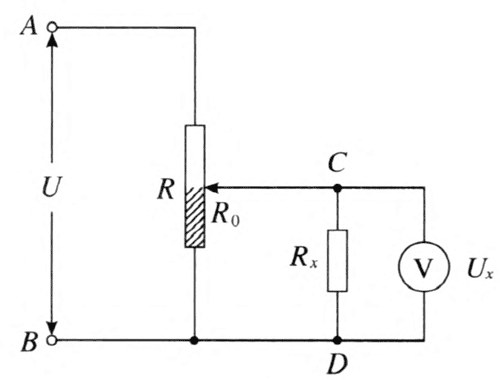
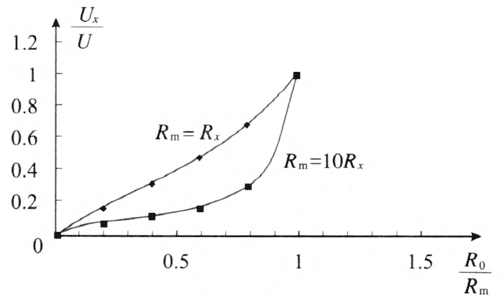
如图 11–24 所示的分压电路，同样采用实验方法可以描出 U_x 随 R₀ 变化的图像（图 11–25）。从图像中不仅可以看出 U_x 的变化范围，还可以看出，R_x 一定时，滑动变阻器的最大阻值越小，图像越接近直线，也就是调节电压越均匀。

（4）电压表和电流表的电路结构

电压表和电流表的改装是串、并联电路的重要应用。这两个电表是中学常用的电学仪表，了解其电路结构和使用方法，也是中学物理的教学目标。知其然，还要知其所以然，本节要使学生从原理角度认识电表。

教科书的思路是：先建立简化模型，从电路角度看，电流表看成能读出自身电流的电阻，电压表看成能读出自身电压的电阻。然后说明电流表和电压表都是由小量程电流表改装的。改装电表又分为四个要点：①表头中的电流越大，指针偏角越大，偏角大小跟电流成正比；②满偏电流、满偏电压的关系满足 I_g = \(\frac{{{U_{\rm{g}}}}}{{{R_{\rm{g}}}}}\)；③为了使电表两端能承受更大的电压，就在表头上串联一个大电阻，为了使电表能承受更大的电流，就在表头上并联一个小电阻；④电流表刻度盘上标的不是表头上流过的电流，而是表头和分流电阻流过的电流之和，电压表也一样，刻度盘标的是表头及分压电阻的电压之和。

 

教学片段

电压表和电流表的电路结构

观察并了解电流表、电压表、小量程电流表（也叫表头）。

建模：从电路角度看，表头可看成一个电阻，是一个能够读出通过其电流的电阻。

表头的电阻记为 R_g，允许通过的最大电流叫满偏电流，用 I_g 表示，满偏电压用 U_g 表示。

表头遵从欧姆定律 I_g = \(\frac{{{U_{\rm{g}}}}}{{{R_{\rm{g}}}}}\)。

问题 1：某个小量程电流表的内阻是 30 Ω，满偏电流是 1 mA，用它能否测量电压？用它测量的最大电压是多少？

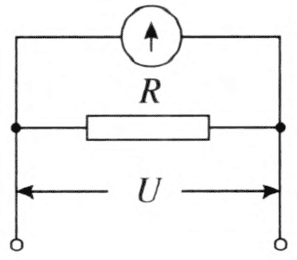
将它跟待测电路并联起来，如图 11–26 所示，读出电流大小，用欧姆定律计算出电压（测量值）

U = I_gR_g

满偏电压（量程）

U_g = I_gR_g = 30 mV

问题 2：请设计一个改装方案，用它能够测量 3 V 的电压。

学生活动：讨论改装方案。

将一个电阻尺跟表头串联起来，如图 11–27 所示，这个串联的电阻叫分压电阻，相同电流下，电路两端的电压就增加了。要使串联电路两端的最大电压为 3 V，则分压电阻需要的阻值为

R = \(\frac{U}{{{I_{\rm{g}}}}}\) – R_g = （\(\frac{3}{{1 \times {{10}^{ - 3}}}}\) − 30）Ω = 2 970 Ω

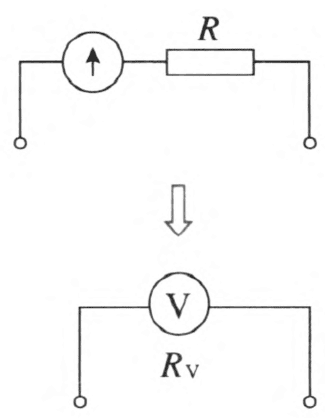
问题 3：改装后的电压表的内阻是多少？

R_V = R_g + R = 3 000 Ω

问题 4：用这个改装后的电压表直接读数，表盘上刻度应该标度电压，刻度会是均匀的吗？

学生讨论刻度是否均匀。

因为 U = IR_V，电压表两端电压跟流过电压表的电流成正比，因此电压表的刻度是均匀的。

---

教学中，为了深化学生对电压表和电流表原理的理解，还可以进一步讨论。下面几个问题供参考：

为了简化问题，我们经常忽略电流表的内阻，称之为理想电流表，把电压表内阻看成无穷大，称之为理想电压表。请大家想想，在什么条件下可以这样做？

当与电流表串联的电阻远远大于电流表内阻，或对实验精度要求不高时，可以忽略电流表内阻。当跟电压表并联的电阻远远小于电压表内阻时，或测量精度要求不高时，可以把电压表看成理想表。

用伏安法测量电阻，采用电流表内接法和外接法的系统误差是怎样的？

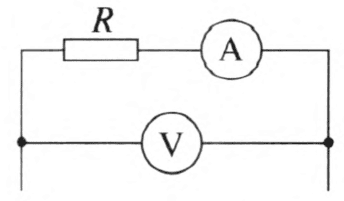
用图 11–28 所示电路测量电阻，如果已知电流表内阻为 R_A，读数为 I，电压表内阻为 Rv，读数为 U，则电阻 R 为多大？

怎样获得两个量程的电流表？画出电路图。

怎样获得两个量程的电压表？画出电路图。

后两个问题可结合课后习题，引导学生讨论。

3．“练习与应用”参考答案与提示

第 1 题是让学生运用串联电路的知识分析限流电路，体会限流电路的限流作用。第2题是让学生运用串、并联电路的知识分析分压电路，体会分压电路的分压作用。第3题说明实际测量中，电压表、电流表（非理想电表）的内阻将影响电路，给测量带来误差，并要求学生能利用串、并联电路的知识分析误差产生的原因。第4、5题是关于有两个量程的电表的问题，要求学生利用串、并联电路的知识解决更为复杂的电表改装问题。

 

1．\(\frac{R}{{R + {R_1}}}\)U ~ U

提示：因为 R₁ 与 R 串联，通过它们的电流相等，可知 \(\frac{{{U_R}}}{R}\) = \(\frac{U}{{R + {R_1}^\prime }}\)，U_R = \(\frac{R}{{R + {R_1}^\prime }}\)U。当滑动变阻器的阻值最小，为 0 时（R₁ʹ = 0），U_R = U；当滑动变阻器的阻值最大，为 R₁ 时，U_R = \(\frac{R}{{R + {R_1}}}\)U。所以，U_R 的变化范围是 \(\frac{R}{{R + {R_1}}}\)U ~ U。

 

2．（1）\(\frac{{{U_1}}}{U}\) = \(\frac{{{R_1}}}{{{R_1} + {R_2}}}\)

（2）设负载电阻为 R₀，变阻器下部分电阻为 R_x，电路结构为 R₀ 与 R_x 并联后，再与（R – R_x）串联。设 R₀ 与 R_x 并联的总电阻为 Rʹ，由串、并联电路的特点可得

U_CD = \(\frac{{R'}}{{R' + (R - {R_x})}}\)U = \(\frac{{\frac{{{R_0}{R_x}}}{{{R_0} + {R_x}}}}}{{\frac{{{R_0}{R_x}}}{{{R_0} + {R_x}}} + (R - {R_x})}}\)U = \(\frac{{{R_0}{R_x}}}{{R{R_0} + R{R_x} - R_x^2}}\)U

当 R_x = 0 时，U_CD = 0；当 R_x = R 时，U_CD = U。所以，U_CD 可以取 0 和 U 之间的任意值。

提示：（1）因为 R₁与 R₂ 串联，通过它们的电流相等，均为 I，可知 U₁ = IR₁，U = I（R₁ + R₂），所以电压之比 \(\frac{{{U_1}}}{U}\) = \(\frac{{{R_1}}}{{{R_1} + {R_2}}}\)。

 

3．80.4 Ω，87.5 Ω

由于电压表和电流表的内阻的影响，两种测量电路都存在系统误差，教科书图 11.4–10 甲中测量值小于真实值，教科书图 11.4–10 乙中测量值大于真实值，但两种电路误差的大小是不一样的。

提示：教科书图 11.4–10 甲中，电流表测得的电流实际上是电压表和电阻并联部分的总电流，所以电阻的测量值为电压表和电阻并联部分的总电阻，即 R_测甲 =\(\frac{{R{R_{\rm{V}}}}}{{R + {R_{\rm{V}}}}}\)  = \(\frac{{87.4 \times {{10}^3}}}{{87.4 + {{10}^3}}}\) Ω = 80.4 Ω。教科书图 11.4–10 乙中，电压表测得的电压实际上是电流表和电阻串联部分的总电压，所以电阻的测量值为电流表和电阻串联部分的总电阻，即 R_测乙 = R + R_A = （87.4 + 0.1）Ω = 87.5 Q。

可以引导学生进一步讨论两种电路的误差大小与待测电阻阻值之间的关系，使学生知道在实际测量中如何选择电路以减小测量误差，为科学探究中电流表的内、外接选择提供理论依据。

在这里，教科书把电流表的内接和外接问题作为串、并联电路在新情境下的一个应用，没有作为一个知识点，因此教学的着眼点应该放在基本规律的运用上。

 

4．9.5×10³ Ω，9.0×10⁴ Ω

提示：当使用 A、B 两个端点时，接 10 V 电压，电流表满偏，即电流为满偏电流，有 I_g（R_g + R₁）= 10 V。解得 R₁ = 9.5×10³ Ω。当使用 A、C 两端点时，I_g（R_g + R₁ + R₂）= 100 V。解得 R₂ = 9.0×10⁴ Ω。

 

5．0.41 Ω，3.67 Ω

提示：当使用 A、B 两个端点时，R₂ 与电流表串联后再与 R₁ 并联，可得 I_g（R_g + R₂）= （I₁ – I_g）R₁。当使用 A、C 两个端点时，R₁ 与 R₂ 串联后再与电流表并联，可得 I_gR_g = （I – I_g）（R₁ + R₂）。联立解得 R₁ = 0.41 Ω，R₂ = 3.67 Ω。

本题的困难在于，学生不容易理解使用 A、B 两个端点时，R₂ 与电流表串联再与 R₁ 并联后也是电流表，能够测量电流。