第十一章 2 导体的电阻
为了减小输电线上电能的损耗,人们尽量把输电线做得粗一点,这是因为导体的电阻与导体的长度、横截面积有关。
那么,它们之间的定量关系是怎样的呢?

选取一个导体,研究导体两端的电压随导体中的电流的变化情况。
图 11.2–1 是根据某次实验结果作出的金属导体 A、B 的 U–I 图像。从图中可以看出,同一个金属导体的 U–I 图像是一条过原点的直线。同一个导体,不管电流、电压怎样变化,电压跟电流之比都是一个常量,这个结论可以写成
\[R = \frac{U}{I}\]
R 是一个只跟导体本身性质有关而与通过的电流无关的物理量。图中不同导体 U–I 图像的倾斜程度不同,表明不同导体的 R 值不同。
从上式可以看出,在电压 U 相同时,R 越大,导体中的电流 I 越小。看来 R 的值反映了导体对电流的阻碍作用,所以,物理学中就把它叫作导体的电阻(resistance)。
导体的电阻到底与导体的哪些因素有关呢?我们可以通过实验来研究导体的电阻与导体的长度、横截面积、材料之间的关系。
在导体的 U–I 图像中,斜率反映了导体电阻的大小。
研究导体电阻与长度、横截面积及材料的定量关系
你认为应该怎样研究导体电阻与长度、横截面积及不同材料之间的关系?说出你的实验方案。
按照你的想法设计表格,进行实验,记录实验数据。分析数据,找出规律。
参考案例
如图 11.2–2,a、b、c、d 是四段不同的金属导体。在长度、横截面积和材料三个因素中,b、c、d 跟 a 相比,分别只有一个因素不同。
考虑到这个实验研究的是导体电阻与长度、横截面积及材料的关系,如果通过比例来表达这种关系,那么实验中就不必测出电阻大小的数值,只需测出电阻之比。图中四段导体是串联的,每段导体两端的电压与它们的电阻成正比,因此测量电阻之比就转化为相应的电压之比。
用电压表分别测量 a、b、c、d 两端的电压,就能知道它们的电阻之比。这样就可以得出长度、横截面积和材料这三个因素与导体电阻的关系。
导体电阻与长度的关系 b 与 a,长度不同,横截面积、材料相同。比较 a、b 的电阻之比与它们的长度之比。
导体电阻与横截面积的关系 c 与 a,横截面积不同,长度、材料相同。比较 a、c 的电阻之比与它们的横截面积之比。
导体电阻与材料的关系 d 与 a,材料不同,长度、横截面积相同。比较 a、d 的电阻是否相等。
改变滑动变阻器滑片的位置,获得多组实验数据。
这个实验得到的是电阻与导线长度、横截面积的比例关系,实验中不必计算电阻大小的数值。
通过上述实验我们发现,导体的电阻与长度、横截面积有定量关系,而且,当导体的长度和横截面积确定后,导体的电阻因材料不同而不同。
通过上述实验可知:同种材料的导体,其电阻 R 与它
的长度 l 成正比,与它的横截面积 S 成反比;导体电阻还与构成它的材料有关。写成公式则是
\[R = \rho \frac{l}{S}\]
进一步实验会发现,同种材料的导体,式中的 ρ 是不变的,不同种材料的导体 ρ 一般不同。这说明 ρ 表征了导体材料的某种特性。
从上述关系式可以看出,在长度、横截面积一定的条件下, ρ 越大,导体的电阻越大。 ρ 叫作这种材料的电阻率(resistivity)。
| 材料 | ρ /(Ω·m) | 材料 | ρ /(Ω·m) |
| 银 | 1.6×10−8 | 铁 | 1.0×10−7 |
| 铜 | 1.7×10−8 | 锰铜合金 | 4.4×10−7 |
| 铝 | 2.9×10−8 | 镍铜合金 | 5.0×10−7 |
| 钨 | 5.3×10−8 | 镍铬合金 | 1.0×10−6 |
从表中可以看出,纯金属的电阻率较小,合金的电阻率较大。连接电路的导线一般用电阻率小的铜来制作,必要时可在导线表面镀银。由于用电器的电阻通常远大于导线的电阻,一般情况下,可以认为导线电阻为 0。
有些合金,如锰铜合金和镍铜合金,电阻率几乎不受温度变化的影响,常用来制作标准电阻。但是,很多金属的电阻率往往随温度的变化而变化。
表格在列出几种材料的电阻率时,标注了温度是 20 ℃,这可能说明了什么?
电阻率与温度的关系
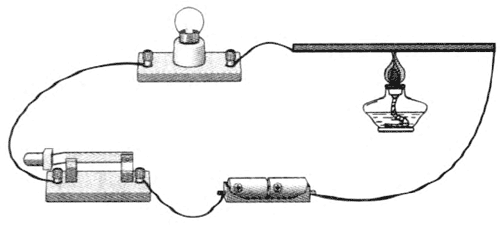
如图 11.2–3,将灯泡的灯丝与小灯泡串联接入电路,使小灯泡发光。用酒精灯给灯丝加热,发现小灯泡变暗。这说明温度升高,灯丝的电阻率变大了。
① 锰铜合金:85% 铜,3% 镍,12% 锰。
镍铜合金:54% 铜,46% 镍。
镍铬合金:67.5% 镍,15% 铬,16% 铁,1.5% 锰。
金属的电阻率随温度的升高而增大。电阻温度计就是利用金属的电阻随温度变化的规律而制成的,用它可以测量很高的温度。精密的电阻温度计是用铂做的。已知铂丝的电阻随温度的变化情况,测出铂丝的电阻就可以知道温度。
当温度降低时,导体的电阻率将会减小。1911 年,科学家们发现一些金属在温度特别低时电阻可以降到 0,这种现象叫作超导现象。金属和合金出现超导现象的温度都很低,到 1986 年为止,人们发现的最高临界温度为 23.2 K(− 249.95℃)。1986年,人类在超导领域取得了重大突破,发现一些铜的氧化物材料可在 44 K(− 229.15℃)左右出现超导现象;1987 年,华裔美国籍科学家朱经武以及中国科学家赵忠贤相继研制出钇—钡—铜—氧系材料,超导转变温度提高到 90 K (− 183.15℃)。若用超导材料形成回路,一旦回路中有了电流,电流就将无损耗地持续下去。根据这一特点,超导材料在发电、输电等方面都会有非常广泛的应用前景。因此科学家还在不断地研究,寻找能够在更高温度下实现超导的导体材料。

伏安特性曲线
在实际应用中,常用横坐标表示电压 U,纵坐标表示电流 I,这样画出的 I–U 图像叫作导体的伏安特性曲线。对于金属导体,在温度没有显著变化时,电阻几乎是不变的(不随电流、电压改变),它的伏安特性曲线是一条过原点的直线,也就是电流 I 与电压 U 成正比(图 11.2–4)。具有这种伏安特性的电学元件叫作线性元件。
实验表明,除金属外,欧姆定律对电解质溶液也适用,但对气态导体(如日光灯管、霓虹灯管中的气体)和半导体元件(图 11.2–5)并不适用。也就是说,在这些情况下电流与电压不成正比,这类电学元件叫作非线性元件。
1.某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在平面直角坐标系中描点,得到了图 11.2–6 中 A、B、C、D 四个点。请比较这四个电阻的大小。
2.在实验室用一段导线连接一个“3 V 0.25 A”的小灯泡做实验时,一般都不会考虑导线的电阻。如果导线的横截面积是 1 mm2,请你估计导线的长度,计算它的电阻,然后说明可以不考虑导线电阻的理由。
3.某人买了 100 m 规格为 4 mm2 的铜导线为 7 A 的空调供电使用。实际上恰好用去了一半导线。如果空调能够正常工作,制冷时在这段导线上损失的电压约是多少?
4.一只鸟站在一条通过 500 A 电流的铜质裸导线上。鸟两爪间的距离是 4 cm,输电线的横截面积是 120 mm2。求鸟两爪之间的电压。
5.某同学想探究导电溶液的电阻随长度、横截面积的变化规律。他拿了一根细橡胶管,里面灌满了盐水,两端用粗铜丝塞住管口,形成一段封闭的盐水柱。他量得盐水柱的长度是 30 cm,并测出盐水柱的电阻等于 R。现握住橡胶管的两端把它拉长,使盐水柱的长度变为 40 cm。如果溶液的电阻随长度、横截面积的变化规律与金属导体相同,此时盐水柱的电阻应该等于多少?
6.如图 11.2–7,一块均匀的长方体样品,长为 a,宽为 b,厚为 c。电流沿 AB 方向时测得样品的电阻为 R,则样品的电阻率是多少?电流沿 CD 方向时样品的电阻是多少?
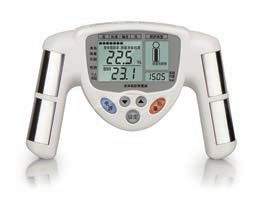
7.人体含水量约为 70%,水中有钠离子、钾离子等离子存在,因此容易导电,脂肪则不容易导电。某脂肪测量仪(图 11.2–8),其原理就是根据人体电阻的大小来判断人体脂肪所占比例。
(1)肥胖的人与消瘦的人电阻不同的主要原因是什么?
(2)激烈运动之后、沐浴之后测量数据会不准确,这可能是什么原因?
第 2 节 导体的电阻 教学建议
1.教学目标
(1)体会物理概念及规律的建立过程,理解电阻的定义。
(2)通过实验探究,了解金属导体的电阻与材料、长度和横截面积的定量关系,体会物理学中控制变量的研究方法。
(3)引导学生观察实验现象,对数据进行分析思考,了解电阻率的物理意义及其与温度的关系。通过查找资料、交流讨论,初步了解超导现象及其应用。
(4)设计实验探究影响导体电阻的因素,同时学习电流表的内外接、滑动变阻器分压及限流接法对电路的影响。
(5)能由伏安特性曲线分析不同导体的导电性能的区别,体会电阻率在科技、生活中的应用。
2.教材分析与教学建议
本节包含的内容比较多,有两个重要概念、一个重要规律和一个学生分组实验。教科书的思路是:首先通过导体 A、B 的U – I 图像给出,对于同一导体,电压跟电流之比 \(\frac{U}{I}\) 是相同的,不同导体,\(\frac{U}{I}\) 一般是不同的,说明 \(\frac{U}{I}\) 表示导体的导电性质,于是用它定义导体的电阻;其次,通过实验研究导体电阻与长度、横截面积及材料的定量关系;最后,通过分析给出反映导体材料对电流阻碍因素的电阻率概念。
本节的重点是电阻的定义及电阻的决定因素;
概念、规律的学习过程是一个循序渐进、螺旋上升的过程,电阻概念的学习最能体现这一点。导体对电流的阻碍作用很复杂,跟长度、横截面积、材料、温度,甚至电压、光照等都有关系,那么用什么来量度呢?跟这些因素有什么定量关系呢?显然,一下子把它们都搞清楚是不可能的,只能一步一步从简单问题出发,逐渐深入。第一步,根据导体的 U – I 图像是正比例图线,定义电阻;第二步,选择锰铜合金丝,用横截面积相同的不同长度的电阻丝做分析和实验,得出 R 跟 l 的关系;第三步,同样选择锰铜合金丝得到 R 跟 S 的关系;第四步,选择锰铜合金丝和镍铬合金丝作对比,发现 R 跟材料有关系,定义出电阻率;第五步,选择灯丝等随温度变化明显的材料,探究电阻率跟温度的关系。电阻和许多因素都可能有关,后边我们会研究各种半导体材料做成的传感器,研究电阻跟光照、压力等的关系。很多概念、规律的学习都是这样一个过程,这其中用到的就是控制变量的方法。
(1)问题引入
本节的引课问题,从输电线的特点出发直接发问,引出本节的重点问题,即电阻跟长度、横截面积的定量关系是什么,引导学生在初中原有知识的基础上深入研究。
在教学中,建议利用材料、长度和横截面积分别不同的导线与小灯泡、电源、开关组成电路,让学生观察不同情况下小灯泡的亮暗程度不同,体会材料、长度、横截面积是影响导线电阻大小的因素。在此基础上提出问题:如何定义不同导体对电流的阻碍作用?为后面电阻的学习做好过渡。
(2)电阻
这里主要讲解为什么要定义电阻,怎么定义电阻,电阻表示什么物理性质。通过分析 U – I 图像的物理意义,然后定义电阻。
教学片段
导体的电阻
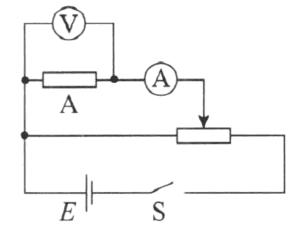
通过实验探究导体对电流的作用。实验电路如图 11–7 所示,电路元件参数(供参考)如下:电源电动势为 6 V;电流表用 0 ~ 0.6 A 量程,内阻约为 0.1 Ω;电压表要求用 0 ~ 3 V 量程,内阻约 3 kΩ;滑动变阻器最大阻值 20 Ω;导体 A 和导体 B 是阻值分别为 5 Ω、10 Ω 的合金丝电阻。
学生分小组做实验。
步骤一:按照电路图 11–7 连接电路,闭合开关前,注意将滑动变阻器的滑片滑到最左端,使得导体 A 两端电压最小。
步骤二:改变滑动变阻器滑片位置,从而改变导体 A 两端电压及导体中电流,在表格中记录对应的电压及电流值。
步骤三:将导体 A 换成导体 B,用同样方式记录相应的电压及屯流值。
实验数据记录表:
导体 A:
| U/V | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 |
| I/A | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
导体 B:
| U/V | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 |
| I/A | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
步骤四:组织学生在坐标纸上画出两次实验的 U–I 图像。
图像如图 11–8 所示。
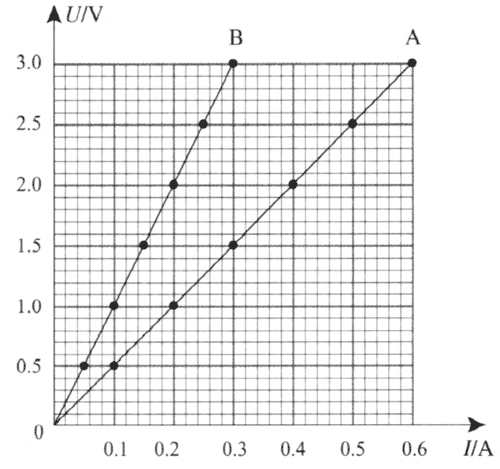
分析讨论图像的含义。从图像可以得出:
①对于导体 A,通过它的电流随所加电压变化,电流跟电压成正比,\(\frac{U}{I}\) = 5 V/A;
②对于导体B,通过它的电流也随电压变化,电流跟电压也成正比,\(\frac{U}{I}\) = 10 V/A。
总结:对于同一导体,\(\frac{U}{I}\) 是同样的,不同导体,\(\frac{U}{I}\) 是不同的,因此 \(\frac{U}{I}\) 是跟电流和电压无关的 量。对于给定的导体,这个比越大,同样电压作用下产生的电流越小。\(\frac{U}{I}\) 反映导体阻碍电流的性质,物理学中就把它定义为导体的电阻。
为了使学生建立电阻的完整概念,还可以从具体数值、单位、物理意义、图像等几个方面进行讨论分析。比如:上述实验中,导体 A、B 的电阻各为多大?谁对电流的阻碍作用更强?人体的电阻大约多大?家用电热器的电阻一般多大?“220 V 40 W”小灯泡正常发光时的电阻多大?在 U–I 图像中,什么表示导体的电阻?
在建立电阻概念后,顺势分析说明欧姆定律的得来:对于一个给定的导体,I = \(\frac{U}{R}\),R 一定,通过它的电流,跟电压 U 成正比;对于不同导体,当 U 一定时,电流跟 R 成反比。这一规律就是我们早就知道的欧姆定律。
教学中可以指出,欧姆定律及电阻定义是同时建立起来的,以消除学生可能出现的误解:先有电阻概念,再实验探究得到电流跟电阻成反比规律。
(3)影响导体电阻的因素
教学中采用实验方法进行教学,将 a、b、c、d 四根不同的金属导体串联在电路中,通过它们的电流相同,这样电压就跟电阻成正比,用电压表测量各导体两端的电压,就可以比较电阻的大小了。a、b 两根导体仅长度不同,可以研究长度对电阻的影响,a、c 导体仅横截面积不同,可以研究横截面积对电阻的影响,a、d 导体仅材料不同,可研究材料对电阻的影响。这种方法比较巧妙地避开了电阻的大小计算。
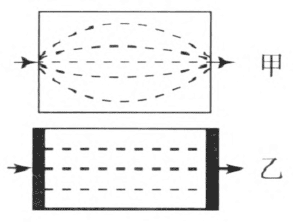
在编制或选择例题、练习题时,要注意导体中的电流场只有在每个横截面上分布相同时,才有 R 跟 S 成正比。我们一般使用的元件是细长条形的,比如导线、电热丝,其内部电流场的分布基本相同。但是如果选择一个长、宽、高差不多的金属块,其内部的电流场大致如图 11–9 甲所示,这时 R = ρ\(\frac{l}{S}\) 不可以直接使用。如果要选择这种形状的导体来做有关 R = ρ\(\frac{l}{S}\) 的巩固练习,需要在导体两端接上片状电极,使导体内部的电流场分布均匀(图 11–9 乙)。
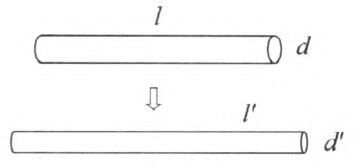
对于联系实际的问题,可以讨论压力传感器中的电阻应变片,其基本原理是通过压力改变金属导体的长度或横截面积来改变电阻,教科书“练习与应用”第 5 题给出了一个非常简单的模拟实验。如图 11–10 所示,在拉力作用下,金属丝变长变细,导致电阻变大,接入电路中的电流或电压就会跟着变化,这就是应变压力传感器的基本原理。
(4)导体的电阻率
对于电阻率概念的建立,教科书采用了实验探究的方法,其教学过程是:实验探究长度、横截面积相同的不同材料的电阻—定义电阻率—分析各种材料的电阻率,找出特点,介绍实际应用一演示实验观察电阻率跟温度的关系一介绍电阻温度计、超导材料。
实验探究材料的电阻率跟温度有关时,除了使用灯泡的灯丝,还可用日光灯的灯丝或细铁丝(直径 0.15 mm、长度 40 cm)代替。
还可以使用铅笔芯演示电阻率随温度增加而减小的现象。如图 11–11 所示,用酒精灯加热铅笔芯,引导学生观察小灯泡会变亮。
这两个实验所需器材比较普通,可以设计成分组体验实验。让学生亲自体验灯丝的电阻率随温度的增加而变大,比如某个小灯泡的灯丝电阻在 20 ℃ 时大约是 36 Ω,在 2 000 ℃ 时能达到大约 360 Ω,而铅笔芯的电阻率随温度的增加而降低,引导学生认识到不同材料电阻率随温度变化的规律是可能相反的。
教科书介绍了超导现象、利用超导材料做成的回路的特点、超导的临界温度及提高临界温度的大致进程。超导是当今科技的热点之一,建议教学中指导学生利用网络、图书、杂志等资源,查找关于超导材料的特性、应用及研究进展情况,并做自主研讨展示活动,培养学生关注科学技术发展的意识和习惯。
(5)伏安特性曲线
教科书在“拓展学习”中介绍了伏安特性曲线,即导体的电流随电压变化的图像叫伏安特性曲线,比较了线性元件和非线性元件的不同点,然后说明了欧姆定律的适用条件。教学中可以组织学生以课题研究的形式做实验探究,描绘电烙铁(或电炉丝)、小灯泡、二极管的伏安特性曲线,学习选择仪器、连接电路、获取数据、描绘曲线的方法,并了解这些常见元件的特点。
3.“练习与应用”参考答案与提示
本节“练习与应用”虽然都以导体电阻规律的理解和应用为主,但每道题的意义不同。第 1 题要求对通过导体的电流与两端电压成正比有较深刻的认识,并能理解伏安特性曲线的物理意义。要求学生能画出伏安特性曲线并利用图线进行分析,可以说这是从 I – U 图像获得有效信息的一种训练。第 2 题直接运用电阻的公式计算导线电阻,同时使学生明白为什么通常情况(包括电学实验中)可以忽略连接用电器的导线的电阻。第 3 题讨论导线上损失的电压,这为介绍远距离输电做了知识准备。因为远距离输电时,导线较长,电阻无法忽略。第 4 题与生活现象相结合,既巩固了导线电阻的计算,又解释了高压线上的鸟为什么没有触电而死。第 5 题将导体电阻的规律应用于导电溶液.进一步巩同这方面的知识。第 6 题对导体电阻的理解要求更高。第 7 题通过某脂肪测量仪,结合导体电阻规律,探究肥胖的人与消瘦的人电阻不同的主要原因及激烈运动之后、沐浴之后该脂肪测量仪测量数据不准确的原因,是将物理规律应用于生活的范例。
1.RA > RB = RC > RD
提示:用直线将图中的四个点与坐标原点连接起来,得到四个电阻的 U – I 图像。B、C 在同一条直线上,因此电阻相同。在三条直线上取一个相同的电压值,可以发现 A 的电流最小,因此电阻最大,D 的电流最大,因此电阻最小。
本题也可以根据直线的斜率判断电阻的大小。
2.小灯泡的电阻为 R = \(\frac{U}{I}\) = \(\frac{3}{0.25}\) Ω = 12 Ω。
估计导线的长度为 10 cm,导线由铜丝制成,铜丝的电阻为 Rʹ = ρ\(\frac{l}{S}\) = 1.7×10−8×\(\frac{{0.1}}{{1 \times {{10}^{ - 6}}}}\) Ω = 1.7×10−3 Ω。
可见,Rʹ 比 R 小得多,故可以不计导线电阻。
3.1.5 V
提示:导线的电阻为 R = ρ\(\frac{l}{S}\) = 1.7×10−8×\(\frac{{50}}{{4 \times {{10}^{ - 6}}}}\) Ω = 0.21 Ω。导线上损失的电压约为 U = IR = 7×0.21 V = 1.5 V。
4.2.9×10−3 V
提示:鸟两爪间导线的电阻为 R = ρ\(\frac{l}{S}\) = 1.7×10−8×\(\frac{{4 \times {{10}^{ - 2}}}}{{120 \times {{10}^{ - 6}}}}\) Ω = 5.7×10−6 Ω。因此鸟两爪间的电压为 U = IR = 500×5.7×10−6 V = 2.9×10−3 V。
5.\(\frac{{16}}{9}\)R
提示:盐水柱的体积不变,所以 lS = lʹSʹ。由于溶液的电阻随长度、横截面积的变化规律与金属导体相同,得 R = ρ \(\frac{l}{S}\),Rʹ = ρ \(\frac{{l'}}{{S'}}\)。因此 \(\frac{{R'}}{R}\) = \(\frac{{l'S}}{{lS'}}\) = (\(\frac{{l'}}{l}\))2 = (\(\frac{4}{3}\))2 = \(\frac{{16}}{9}\),Rʹ = \(\frac{{16}}{9}\)R。
本题的隐含条件是盐水柱的体积不变,重在培养学生的模型建构能力。
6.\(\frac{{bc}}{a}\) R;(\(\frac{{b}}{a}\))2R
提示:沿 AB 方向,则 l = a,S = bc,由 R = ρ\(\frac{l}{S}\) 得 ρ = \(\frac{SR}{l}\) = \(\frac{{bc}}{a}\)R。沿 CD 方向,lʹ = b,Sʹ = ac,故电阻为 Rʹ = ρ\(\frac{{b}}{ac}\) = (\(\frac{{b}}{a}\))2R。
导体电阻公式中长度,是沿电流方向的长度,横截面积 S 是垂直电流方向的导体面积。两种情形下,电阻率相同是解题的突破口。
7.(1)肥胖的人体内脂肪含量多,而脂肪不容易导电,因而肥胖的人的电阻大。
(2)激烈运动或沐浴之后,人的外表会附着容易导电的钠离子、钾离子等离子,使得同一人体的电阻变小,这时用脂肪测量仪得出的结果自然就不准确。
说明:由题设给定条件解答第(1)问,由原理中包含的物理规律解答第(2)问,是对学生获取信息能力的训练,对理解能力和科学探究的较好巩固。
发布时间:2020/6/28 下午9:13:03 阅读次数:6893
