必修 2 课题研究
课题研究
关于甩手动作的物理原理研究
问题的提出
人们在长期生活和劳动中,形成了许多动作习惯。这些习惯的动作,之所以能有效地达到我们动作的目的,其背后必定有相关物理原理的支撑。剖析这些动作的物理原理,无论是对提高竞技体育的成绩,还是优化科技产品的设计都是有价值的。特别是作为物理课程的学习者,研究人体动作的物理原理,对增强理论联系实际的意识和发展科学思维能力都具有积极的意义。
本课题研究人甩手动作的物理原理。例如,要把湿手上的水甩掉,人通常的甩手动作是怎样的?为什么这样的动作容易把水甩掉?
甩手动作的实验记录
图研–1 是一幅记录甩手动作的图片,体现了把手指上的水滴甩掉的过程。这幅图片是由家用摄像机拍摄视频后制作的(每秒 25 帧,也可以利用手机的摄像功能拍摄),它真实地记录了手臂各部位在不同时刻的位置信息。如果知道摄像时的帧频,就知道相邻两动作之间的时间间隔,便可以对各部位的位置-时间关系进行分析,从而发现隐含在甩手动作中的物理原理。
甩手动作的运动模型分析
从分析运动的视角看,人的上肢可以认为由上臂、前臂和手掌组成。现把图研–1 按上臂、前臂、手掌的结构简化为图研–2。可以看出,在甩手过程中,上臂以肩关节 O1 为转动轴转动,此时肘关节 O2 在做圆周运动,圆心为 O1 、半径为
r1 ;腕关节 O3 相对 O2 的运动,是以 O2 为圆心、r2 为半径的圆周运动;手指上某水滴 P 相对腕关节的运动也是圆周运动,其圆心为 O3 、半径为 r3 。这样,P 点除了绕 O3 做圆周运动之外,同时还叠加了 O3 相对 O2 的运动和 O2 相对 O1 的运动,因此,P 点具有较大的线速度。由于 P 点绕 O3 做圆周运动的半径 r3 很小,由向心力公式可知,如果水滴 P 要继续停留在手上,需要很大的向心力。否则水滴便会做离心运动,飞离手指。
甩手动作的数据分析
1.测量照片与实物尺寸的缩放比例。通过对照片的测量了解照片所反映的实物尺寸,首先要知道照片尺寸与实物尺寸的缩放比例。为此,测量实验者手臂自然下垂时肩膀到指尖的实际长度,实测为 65 cm(图研–3),再测量照片中的相应位置的长度,便得到照片与实物的缩放比例。知道这个比例,测量照片上某两点之间长度的值,就可以算出这两点在实验时的真实距离。
2.估算指尖的最大向心加速度。用 a向 = \(\dfrac{{{v^2}}}{r}\)公式来计算指尖的最大向心加速度。
如图研–1 所示,A、B、C 是甩手动作最后 3 帧照片指尖的位置,测得 A、B 之间的距离为 26 cm,已知相邻两帧之间的时间间隔为 0.04 s。由此可以计算指尖在 A、B 间运动的平均速度为 6.5 m/s,粗略认为这就是甩手动作最后阶段指尖作圆周运动的线速度。
下面需要测量指尖在 AB 运动过程最后阶段的运动半径。可以根据照片建构 A、B 之间的运动模型:开始阶段,指尖 A 以肘关节 M 为圆心做圆周运动,到接近 B 的最后时刻,指尖以腕关节 N为圆心做圆周运动。根据上述模型,指尖在 B 点附近做曲线运动的半径等于图中 BN 的长度,测得为 17 cm。由此计算指尖的向心加速度约为
\[{a_向} = \frac{{{v^2}}}{r} = \frac{{{{6.5}^2}}}{{0.17}}\;{\rm{m/}}{{\rm{s}}^{\rm{2}}} = 249\;{\rm{m/}}{{\rm{s}}^{\rm{2}}} \approx 25g\]
对数据分析的实验检验
指尖的向心加速度约 25g,真有这么大的加速度吗?在手机上安装相应的应用程序,用手机的加速度传感器进行检验。

在甩手动作的末段,指尖急速停下,因此指尖还有较大的切向加速度。指尖的加速度是向心加速度和切向加速度的矢量和。有兴趣的同学可以作进一步的估算。
因为很难把手机固定在指尖,所以测量指尖部位的加速度不容易操作。可以考虑用手机测量手腕部位(图研–1 中的 N 点)做圆周运动的向心加速度。如图研–4 所示,用手指和手掌握住手机,使手机中心对准腕关节,且手机的长边跟前臂平行。(不同型号的手机,加速度传感器所在的位置可能不同。请查找资料,采用合适的握法握紧手机,完成实验。)
甩手时(此时腕关节不转动,因为测的是手腕部位的加速度),手机显示了 x、y、z 三个坐标轴方向的加速度值(图研–5)。其中 y 方向的加速度(绿色图线)是手腕部位的向心加速度,最大值约等于 32 m/s2。
从图研–1 可以测出 AB 的弧长大约是 N 点在相同时间内通过弧长的 2.2 倍,B 点的线速度 vB 也为 N 点线速度 vN 的 2.2 倍,vB = 2.2vN 。B 点做圆周运动的半径 NB 大约是 N 点做圆周运动半径 MN 的 \(\dfrac{3}{5}\),rB = \(\dfrac{3}{5}\)rN。由公式 a向 = \(\dfrac{{{v^2}}}{r}\)可以得出
\[{a_B} = \dfrac{{{v^2}}}{r} = \dfrac{{{{(2.2{v_N})}^2}}}{{\dfrac{3}{5}{r_N}}} = 8{a_N}\]
即指尖 B 点的向心加速度大约是手腕 N 点的 8 倍,为 8 ×32 m/s2 = 258 m/s2,与数据分析所得的 a向 = 249 m/s2 很接近。因此,数据分析的结果基本可信。
结论
指尖的向心加速度最大时竟然达到重力加速度的 25 倍,水滴之间的相互作用力无法满足这种运动的受力要求,因此手上的水滴被甩出。
甩手时的指尖之所以能产生这么大的向心加速度,这里包含着两个方面的物理原理。
第一,利用了运动的合成。手指对手腕、手腕对前臂、前臂对上臂的运动都是在最后阶段达到最大,三个运动的叠加使手指在甩手过程的最后获得了最大瞬时速度,从图研–1 中 A、B 之间的距离突然变大可以体会到这点。
第二,利用了圆周运动。手臂运动的最后一刻,指尖做圆周运动,圆心是腕关节,半径很小,由此产生了巨大的向心加速度。
以上研究给我们带来了重要启示:人们(以及动物)

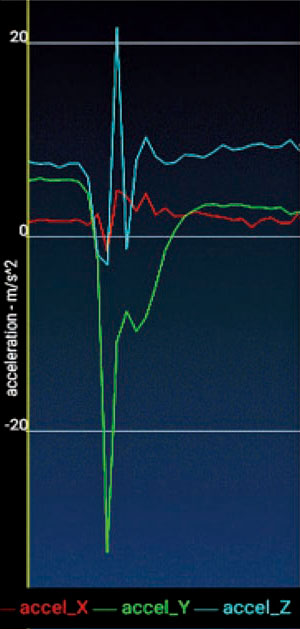
图研–5 中有一条蓝色的曲线,记录的是手腕部位的切向加速度,本研究暂忽略。
的动作习惯是通过有效经验的积累形成的,其中隐藏着许多物理原理。对这些动作进行物理原理研究,不仅可以进一步从原理上改进动作的效果(如竞技体育的动作训练),还可以从“仿生”的角度对人类工具作进一步的优化。
掷标枪动作的物理原理研究
研究内容
掷标枪竞赛是奥运会田径竞赛项目,掷标枪有以下关键动作。
1.握枪:标枪上缠有粗绳,拇指和食指握在缠绳把手末端边沿,其余手指顺食指方向握在缠绳把手上面(图研–6)。
2.助跑:采用直线助跑,助跑后期,持枪手臂向后引枪。
3.投掷:在后仰基础上,支撑腿迅速有力地蹬伸,同时以胸部和肩带动投掷臂向前做爆发性“鞭打”动作,将标枪快速掷出(图研–7)。
以上动作,包含了诸多物理原理。本研究旨在深入剖析这些动作的物理原理。

图研–7 掷标枪
发布时间:2020/6/2 下午9:52:50 阅读次数:4765
