第八章 3 动能和动能定理

问题

物体的动能跟物体的质量和速度都有关系。物体的质量越大，速度越大，它的动能就越大。炮弹在炮筒内推力的作用下速度越来越大，动能增加。这种情况下推力对物体做了功。

你还能举出其他例子，说明动能和力做的功有关吗？这对于定量研究动能有什么启发呢？

动能的表达式

大量实例说明，物体动能的变化和力对物体做的功密切相关。因此，研究物体的动能离不开对力做功的分析。这与上一节研究重力势能的思路是一致的。

质量为 m 的某物体在光滑水平面上运动，在与运动方向相同的恒力 F 的作用下发生一段位移 l，速度由 v₁ 增加到 v₂ （图 8.3-1）。

在这个过程中，恒力 F 做的功 W＝Fl，根据牛顿第二定律，有

\[F = ma\]

再根据匀变速直线运动的速度与位移的关系式，有

\[l = \frac{{v_2^2 - v_1^2}}{{2a}}\]

把 F、l 的表达式代入W＝Fl中，可得 F 做的功

\[W = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2\]

从上式可以看出，“\(\frac{1}{2}\)mv²”很可能是一个具有特定意义的物理量，因为这个量在过程终了与过程开始时的差，正好等于力对物体做的功。在物理学中就用“\(\frac{1}{2}\)mv²”这个量表示物体的动能（kinetic energy），用符号 E_k 表示。于是我们说，质量为 m 的物体，以速度 v 运动时的动能是

\[{E_k} = \frac{1}{2}m{v^2}\]

动能是标量，它的单位与功的单位相同，在国际单位制中都是焦耳，这是因为

1 kg（m/s）² ＝1 N·m＝1 J

思考与讨论

2016年8月16日，我国成功发射首颗量子科学实验卫星“墨子号”，它的质量为 631 kg，某时刻它的速度大小为 7.6 km/s，此时它的动能是多少？

动能定理

在得到动能的表达式后，\(\frac{1}{2}\)mv₂² －\(\frac{1}{2}\)mv₁²可以写成

\[W = {E_{k2}} - {E_{k1}}\]

其中 E_k2 表示一个过程的末动能，E_k1 表示这个过程的初动能。

这个关系表明，力在一个过程中对物体做的功，等于物体在这个过程中动能的变化。这个结论叫作动能定理（theorem of kinetic energy）。

如果物体受到几个力的共同作用，动能定理中的力对物体做的功 W 即为合力做的功，它等于各个力做功的代数和。

这里，动能定理是在物体受恒力作用，并且做直线运动的情况下得到的。 当物体受变力作用，或做曲线运动时，我们可以采用把整个过程分成许多小段，认为物体在每小段运动中受到的是恒力，运动的轨迹是直线，把这些小段中力做的功相加，这样也能得到动能定理。

因为动能定理适用于变力做功和曲线运动的情况，所以在解决一些实际的力学问题时，它得到了广泛的应用。

例题1

一架喷气式飞机，质量 m 为 7.0×10⁴ kg，起飞过程中从静止开始滑跑。当位移 l 达到 2.5×10³ m 时，速度达到起飞速度 80 m/s。在此过程中，飞机受到的平均阻力是飞机所受重力的\(\frac{1}{50}\) 。g 取 10 m/s²，求飞机平均牵引力的大小。

分析 本题已知飞机滑跑过程的始、末速度，因而能够知道它在滑跑过程中增加的动能。根据动能定理，动能的增加等于牵引力做功和阻力做功的代数和。

如图 8.3-2，在整个过程中，牵引力对飞机做正功、阻力做负功。由于飞机的位移和所受阻力已知，因而可以求得牵引力的大小。

解 以飞机为研究对象， 设飞机滑跑的方向为x轴正方向。飞机的初动能 E_k1 ＝0，末动能 E_k2 ＝\(\frac{1}{2}\)mv²，合力 F 做的功

\[W = Fl\]

根据动能定理 W ＝ E_k2 － E_k1 ，有

\[Fl = \frac{1}{2}m{v^2} - 0\]

由于

F ＝ F_牵 － F_阻 ，F _阻 ＝ kmg，k ＝\(\frac{1}{50}\)

则

\[{F_牵} = \frac{{m{v^2}}}{{2l}} + kmg\]

把数值代入后得到

F _牵 ＝ 1.04×10⁵ N

飞机平均牵引力的大小是 1.04×10⁵ N。

从这个例题可以看出，动能定理不涉及物体运动过程中的加速度和时间，因此用它处理问题常常比较方便。

在应用动能定理时还应该注意到，力对物体做的功可以为正值，也可以为负值。合力做正功时，物体的动能增加；合力做负功时，物体的动能减少。

【例题2】

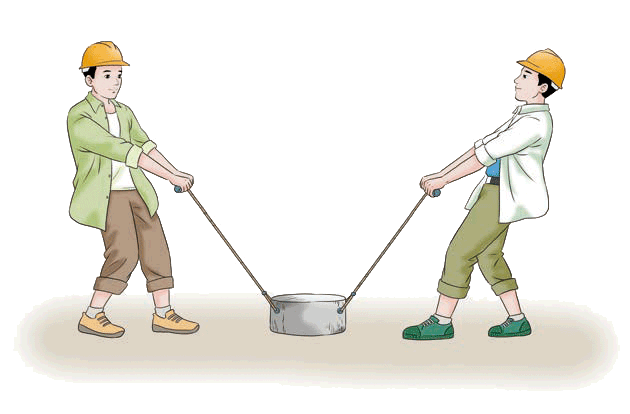
人们有时用“打夯”的方式把松散的地面夯实（图8.3-3）。设某次打夯符合以下模型：两人同时通过绳子对重物各施加一个力，力的大小均为320 N，方向都与竖直方向成37°，重物离开地面30 cm 后人停止施力，最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg，g取10 m/s²，cos 37°＝0.8。求：（1）重物刚落地时的速度是多大？（2）重物对地面的平均冲击力是多大？

分析 如图8.3-4，甲表示重物在地面上受到人的作用力，乙表示上升30 cm后人停止施力，丙表示刚落地，丁表示砸深地面2 cm后静止。

重物落地时的速度，即丙中重物的速度，可以对从甲至丙这一过程应用动能定理来求解。重物对地面冲击力的大小与从丙至丁这一过程中重物所受阻力的大小相等，可以对这一过程应用动能定理来求解。

解 （1）两根绳子对重物的合力

F_合＝ 2 F cos 37°＝2×320×0.8 N＝512 N

由甲至丙只有绳子的拉力做功，应用动能定理可得

\[\begin{array}{l}{F_合}l = \frac{1}{2}m{v^2}\\v = \sqrt {\frac{{2{F_合}l}}{m}} = \sqrt {\frac{{2 \times 512 \times 0.3}}{{50}}} = 2.5{\rm{m/s}}\end{array}\]

（2）由丙到丁的过程中，应用动能定理可得

\[\begin{array}{l}mgl' - {F_阻}l' = 0 - \frac{1}{2}m{v^2}\\{F_阻} = mg + \frac{{m{v^2}}}{{2l'}} = (50 \times 10 + \frac{{50 \times {{2.5}^2}}}{{2 \times 0.02}}){\rm{N}} = 8.3 \times {10^3}{\rm{N}}\end{array}\]

重物落地时的速度大小为2.5 m/s，对地面的平均冲击力的大小为8.3×10³ N。

科学方法

演绎推理

演绎推理是从一般性结论推出个别性结论的方法，即从已知的某些一般原理、定理、法则、公理或科学概念出发，推出新结论的一种思维活动。

比如，在“动能定理”的推导过程中，其出发点是将牛顿第二定律作为已知的知识来考虑，然后经历一系列数学推导，从而得到新的结论——动能定理。

练习与应用

1．改变汽车的质量和速度，都可能使汽车的动能发生改变。在下列几种情况下，汽车的动能各是原来的几倍？

A．质量不变，速度增大到原来的 2 倍

B．速度不变，质量增大到原来的 2 倍

C．质量减半，速度增大到原来的 4 倍

D．速度减半，质量增大到原来的 4 倍

2．把一辆汽车的速度从 10 km/h 加速到20 km/h，或者从 50 km/h 加速到 60 km/h，哪种情况做的功比较多？通过计算说明。

3．质量为 8 g 的子弹，以 300 m/s 的速度射入厚度为 5 cm 的固定木板（图 8.3-5），射穿后的速度是 100 m/s。子弹射穿木板的过程中受到的平均阻力是多大？

4．我们曾在第四章中用牛顿运动定律解答过一个问题：民航客机机舱紧急出口的气囊是一条连接出口与底面的斜面，若斜面高 3.2 m，斜面长 6.5 m，质量为 60 kg 的人沿斜面滑下时所受的阻力是 240 N，求人滑至底端时的速度大小，g 取 10 m/s² 。请用动能定理解答。

5．运动员把质量为 400 g 的足球踢出后（图 8.3-6），某人观察它在空中的飞行情况，估计上升的最大高度是 5 m，在最高点的速度为20 m/s。不考虑空气阻力，g 取 10 m/s²。请你根据这个估计，计算运动员踢球时对足球做的功。

发布时间：2020/4/5 下午1:42:28  阅读次数：4242