第四章 6 超重与失重
问题
站在体重计上向下蹲，你会发现，在下蹲的过程中，体重计的示数先变小，后变大，再变小。当人静止后，保持某一数值不变。这是为什么呢？
重力的测量
在地球表面附近，物体由于地球的吸引而受到重力。测量重力常用两种方法：一种方法是，先测量物体做自由落体运动的加速度g，再用天平测量物体的质量，利用牛顿第二定律可得
G = mg
另一种方法是，利用力的平衡条件对重力进行测量。将待测物体悬挂或放置在测力计上，使它处于静止状态。这时物体所受的重力和测力计对物体的拉力或支持力的大小相等，测力计的示数反映了物体所受的重力大小。这是测量重力最常用的方法。
超重和失重
人站在体重计上向下蹲的过程中，为什么体重计的示数会变化呢？
体重计的示数称为视重，反映了人对体重计的压力。根据牛顿第三定律，人对体重计的压力与体重计对人的支持力FN大小相等，方向相反。
如图 4.6–1，选取人为研究对象。人体受到重力mg和体重计对人的支持力FN，这两个力的共同作用使人在下蹲的过程中，先后经历加速、减速和静止三个阶段。
设竖直向下方向为坐标轴正方向。
人加速向下运动的过程中（图 4.6–2），根据牛顿第二定律，有
mg − FN ＝ma
FN ＝ m（g − a）< mg
即体重计的示数所反映的视重（力）小于人所受的重力。
物体对支持物的压力（或对悬挂物的拉力）小于物体所受重力的现象，叫作失重（weightlessness）现象。
同理，人减速向下运动的过程中（图 4.6–3），加速度方向与运动方向相反，有
mg－FN＝－ma
FN＝m（g＋a）>mg
此时，体重计的示数大于人受到的重力。
物体对支持物的压力（或对悬挂物的拉力）大于物体所受重力的现象，叫作超重（overweight）现象。
当人相对于体重计静止不动时，有
FN＝mg
思考与讨论
人站在力传感器上完成下蹲动作。观察计算机采集的图线。图 4.6–4 呈现的是某人下蹲过程中力传感器的示数随时间变化的情况。很明显，图线直观地描绘了人在下蹲过程中力传感器的示数先变小，后变大，再变小，最后保持某一数值不变的全过程。
如图 4.6–5，图线显示的是某人站在力传感器上，先“下蹲”后“站起”过程中力传感器的示数随时间的变化情况。
请你分析力传感器上的人“站起”过程中超重和失重的情况。
可见，人的运动状态对体重计上显示出的结果是有影响的。那么，如果站在体重计上的人既不蹲下，也不站起，体重计上的示数就不会变吗？
做一做
在电梯地板上放一台体重计。站在体重计上，观察电梯启动、制动和运行过程中体重计示数的变化。
【例题】
设某人的质量为 60 kg，站在电梯内的水平地板上，当电梯以 0.25 m/s2 的加速度匀加速上升时，求人对电梯的压力。g 取 9.8 m/s2。
分析 人站在电梯内的水平地板上，随电梯上升过程中受到两个力的作用：重力 mg 和地板的支持力 FN，受力分析如图 4.6–6 所示。
解 设竖直向上方向为坐标轴正方向。
根据牛顿第二定律，有
FN － mg ＝ ma
FN ＝ m（g＋a） ＝ 60×（9.8＋0.25）N ＝ 603 N
根据牛顿第三定律，人对电梯地板的压力为
FN′ ＝ －FN ＝ －603 N
人对电梯的压力大小为 603 N，方向竖直向下。
这个结果说明，当人与电梯共同向上加速或向下减速运动时，FN′ > G，人对电梯的压力将大于人所受的重力，出现超重现象。
同理，如果电梯加速下降（或减速上升），FN′ < G，人对电梯的压力将小于人的重力，出现失重现象。
如果人在加速下降的过程中加速度a＝g，那么，体重计的示数为0。这时物体对支持物（或悬挂物）完全没有作用力，这种现象被叫作完全失重状态。
实际中有许多领域涉及超重和失重现象。例如，火箭发射时向上的加速度很大，火箭底部所承受的压力要比静止时大得多。如果是载人航天，在火箭发射阶段，航天员要承受数倍于自身体重的压力。只有很好地研究材料、机械结构、人体自身所能承受的压力问题，才能使火箭成功发射、航天员顺利飞向太空。
航天器在太空轨道上绕地球或其他天体运行时，航天器内的物体将处于完全失重状态。完全失重时，物体将飘浮在空中，液滴呈球形（图 4.6–7），气泡在液体中将不会上浮，走路时稍有不慎，将会“上不着天，下不着地”……
超重和失重现象在实际中还有许多，请你通过读书、上网、请教专业人员等多种途径进一步学习和了解。
练习与应用
1．当在盛水的塑料瓶壁上扎一个小孔时，水会从小孔喷出，但释放水瓶，让水瓶自由下落，水却不会从小孔流出。这是为什么？
2．蹦极是一项极限体育项目。运动员从高处跳下，在弹性绳被拉直前做自由落体运动；当弹性绳被拉直后，在弹性绳的缓冲作用下，运动员下降速度先增加再减小逐渐减为0。下降过程中，运动员在什么阶段分别处于超重、失重状态？
3．火箭发射时，宇航员要承受超重的考验。某火箭发射的过程中，有一段时间的加速度达到 3.5g，平时重力为 10 N 的体内脏器，在该超重过程中需要的支持力有多大？
4．一种巨型娱乐器械可以使人体验超重和失重状态（图 4.6–8）。一个可乘坐二十多个人的环形座舱套装在竖直柱子上，由升降机送上几十米的高处，然后让座舱自由落下。落到一定位置时，制动系统启动，到地面时刚好停下。已知座舱开始下落时的高度为 76 m，当落到离地面 28 m 的位置时开始制动，座舱做匀减速运动。若座舱中某人用手托着质量为 0.2 kg 的手机，当座舱落到离地面 50 m 的位置时，手的感觉如何？当座舱落到离地面 15 m 的位置时，手要用多大的力才能托住手机？
5．小明住的楼房中有一部电梯，小明用了两种方法估测电梯在加速和减速过程中的加速度。
方法1 用测力计悬吊一个重物，保持测力计相对电梯静止，测得电梯上升加速时测力计读数为 G1，减速时为 G2。小明了解到该电梯加速和减速过程的加速度大小是相同的。由此，请估算电梯变速运动时加速度有多大？
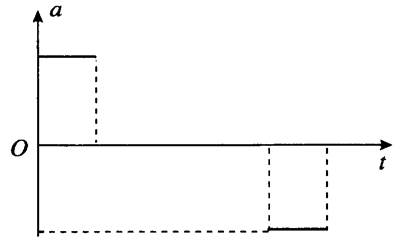
方法2 用手机的加速度传感器测量电梯上升中由起动到停止的加速度。请描述此过程电梯的a-t图像是怎样的。再用手机实地测一下看是怎样的。
第 6 节 超重和失重 教学参考
1．教学目标
（1）通过体验或者实验，认识超重和失重现象。
（2）通过在电梯里观察体重计示数或其他方式发现超重和失重现象产生的条件，并应用牛顿运动定律分析超重和失重现象发生的动力学原因，理解超重和失重现象的本质，培养学生从实际情境中捕捉信息、发现问题并提出问题的能力。
（3）通过查阅资料、分享和交流，了解超重和失重现象在各个领域中的应用，解释生活中的超重和失重现象，培养学生用科学知识解释生活现象的能力，激发学生的学习热情和兴趣，形成良好的科学态度与责任。
2．教材分析与教学建议
教科书中将“超重与失重”以单独一节的形式呈现出来，注重学生在学习超重和失重过程中的体验和发现过程，强化应用牛顿运动定律分析超重和失重过程的方法。
教科书通过让学生站在体重计上向下蹲的过程中观察体重计示数的变化，引发疑问，强调学生的参与、体验与思考。在学生展开活动之前，教科书帮助学生明确了两种常见的测量重力的方法，为学生后续利用体重计寻找超重和失重产生的条件并理解超重和失重搭建了台阶。在“超重和失重”中，教科书引导学生利用牛顿运动定律对体重计上的人进行分析，并根据体重计的示数与重力的关系，介绍了超重现象和失重现象。教科书在“思考与讨论”栏目中将体重计示数变化图像化，并引导学生分析从体重计上“站起”过程中超重和失重的情况，强调了学生的分析过程。再通过“做一做”栏目和所给的例题，再一次体验超重和失重的过程，强化了牛顿运动定律的应用。教科书最后提出了超重和失重现象在许多领域中都有所应用，引导学生通过多种方式进行进一步的学习。
学习牛顿运动定律及应用牛顿运动定律解决问题是本章的核心内容，因此应用规律分析超重和失重现象自然是本节的教学重点。由于超重和失重现在已经演化成了生活语言，与物理学中超重和失重本来的意义有较大的不同，因此引导学生对超重和失重的物理内涵有清晰的认识是本节的教学难点。
（1）问题引入
教科书通过学生在体重计上向下蹲的过程，创设了真实的、学生可以参与的情境。在此基础上提出了关于示数变化的问题，激发了学生学习兴趣，引发学生思考，充分体现了学生学习的主体性和参与性。
当然，在教学中播放视频或者演汞实验也可以激发学生的学习兴趣，引发学生的思考，以下教学片段采用了演示实验的方式引出学习内容。
教学片段
演示超重和失重现象
如图 4–5 所示，在一个台秤上放置一个木箱，箱内顶部悬挂一根弹簧，弹簧下系一个重物（箱前面封闭，学生看不到弹簧和重物）。重物静止时，台秤上的指针指向某一固定的位置。
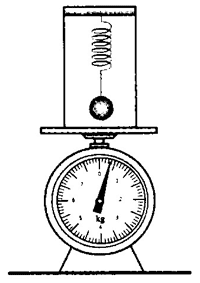
教师让重物上下振动（学生依然不可见），引导学生观察台秤示数的变化情况。提出引导学生思考的问题：你能猜出箱子内部是什么结构吗？
教师展示木箱的内部结构后，提出问题：你能说说什么情况下台秤的示数最大、什么情况下台秤的示数最小吗？
引导学生利用牛顿运动定律分析得出结论。将木箱背面转过来，通过照相的方式记录球在不同位置时台秤的示数来验证结论。
（2）重力的测量
重力的测量这一部分内容提出了在地球表面附近测量重力的两种方法：第一种方法是测量物体质量，再乘以所测量的重力加速度得到重力；第二种方法是利用力的平衡条件来测量重力。
在教学中，建议教师可以组织学生基于以下两个问题阅读教科书：测量物体重力的方法有哪些？测力计测量物体重力的原理是什么？
以下教学片段引导学生体会弹簧测力计测量物体重力是利用了力的平衡条件来测量的，为学生理觯体重计上的超重和失重现象作好铺垫。
教学片段
用弹簧测力计测量钩码的重力
教师提出问题：使用弹簧测力计测量物体所受的重力时，为什么要让物体保持静止时读数？如果不保持静止可能会发生什么现象？
学生体验发现弹簧测力计保持静止状态时，重物受力满足平衡条件，弹簧测力计的示数与物体重力相等。如果弹簧测力计在竖直方向运动，则会出现示数波动的情况。
学生进行实验：①测量钩码的重力；②将弹簧测力计连同钩码向上加速运动，观察弹簧秤示数的变化；③让弹簧测力计连同钩码向下加速运动，观察弹测力计示数的变化。学生发现当钩码向上或向下运动时，弹簧测力计的读数有时大于钩码的重力，有时小于钩码的重力。
教师引导学生思考讨论：在什么情况下弹簧测力计的示数大于物体所受的重力？在什么情况下弹簧测力计的示数小于物体所受的重力？
（3）超重和失重
在这部分内容中，建议教师在教学中注意以下几点：
第一，建议先让学生亲自参与体验超重和失重的过程，再引导学生应用牛顿运动定律进行分析与解释，强化学生的体验过程，这有助于激发学生学习的主动性，培养学生应用物理知识解决生活现象的意识。
以下教学片段针对学生活动设计了引导学生观察、思考和分析的问题，引导学生通过观察、记录、分析和总结得出结论。
教学片段
观察电梯中的超重和失重现象
课前组织部分学生将体重计搬到电梯中，让一位同学站在体重计上，然后让电梯从静止状态开始从一楼升到五楼，再从五楼下降到一楼，要求学生观察其示数变化，用手机将体重计示数变化情况拍摄下来。
教师在课堂上将拍摄到的示数情况投影到屏幕上，同时请学生解说实验过程中观察到的现象。引导学生分析如下问题：
①电梯从一楼由静止开始上升至五楼再由五楼下降至一楼的过程中，经历了哪些运动过程？
②各个过程分别是什么样的运动？
③在各个过程中体重计的示数情况怎样？
④物体出现超重和失重状态与哪个物理量有关？
在充分讨论的基础上，由学生完成表 4–3。通过填表，学生很容易地排除了速度方向，而准确地定位到加速度的方向上。从而总结得出以下结论：当电梯具有向上的加速度时，人处于超重状态；当电梯具有向下的加速度时，人处于失重状态。
表 4–3
|
运动状态 |
运动性质 |
示数情况 |
加速度方向 |
|
静止 |
平衡状态 |
正常 |
/ |
|
上升 |
加速上升 |
偏大 |
向上 |
|
匀速上升 |
正常 |
/ |
|
|
减速上升 |
偏小 |
向下 |
|
|
下降 |
加速下降 |
偏小 |
向下 |
|
匀速下降 |
正常 |
/ |
|
|
减速下降 |
偏大 |
向上 |
第二，在引导学生利用牛顿运动定律分析超重和失重的过程中，应该提醒学生正确运用牛顿第三定律。让学生注意到人加速向下运动的过程中有 FN < mg，这里的 FN 是体重计给人的支持力，与失重概念中物体对支持物的压力是互为作用力和反作用力的。
第三，引导学生准确理解超重和失重的概念。学生容易出现“超重是重力增加，失重是重力减少”的误区。教师可以在引导学生利用牛顿运动定律分析物体受力情况后提出这样的问题让学生来讨论：物体的超重和失重是物体所受的重力发生了变化吗？
学生经过讨论后会发现，在产生超重和失重现象的过程中，只要物体的位置相对地球没有发生较大的改变，物体所受的重力并不会改变，只是对支持物的压力或对悬挂物的拉力发生了变化。
第四，在分析超重和失重两种现象的过程中，建议保持学生自主学习的空间。依据学生的条件不同，可以由教师引导学生分析，或者与学生一起讨论分析超重或失重现象中的一种，而让学生独立分析和推理另一种现象，培养学生的方法迁移能力。
第五，对于完全失重，可以让学生观看航天员生活的视频，让学生通过更多的途径简单了解。
3．“练习与应用”参考答案与提示
本节共 5 道习题。第 1 题以塑料瓶为素材，通过对生活现象的探究，定性解释失重现象。第 2 题以蹦极运动为背景，通过对不同阶段运动情况分析，判断运动员在不同阶段是处于超重状态还是失重状态，加深对超重和失重的理解。第 3 题通过定量计算让学生理解超重，感受在火箭加速阶段航天员的身体器官要承受的压力。第 4 题以体验超重和失重的升降机为背景，从定性和定量两个方面理解超重和失重，加深对力和运动的关系的理解与灵活应用。第 5 题通过测量电梯中的加速度，引导学生探究常见生活现象中所蕴含的物理规律，应用所学物理知识解释实际问题，达到学以致用的目的。
1．当水瓶自由下落时，小孔没有水喷出，是因为水和水瓶都处于完全失重状态，水和水瓶下落的加速度都等于重力加速度，下落的快慢程度相同，故水不会从瓶中流出。
2．下降过程中，弹性绳被拉直前的自由落体运动阶段，以及弹性绳被拉直后运动员下降速度增加的阶段，因加速度方向向下，故均处于失重状态；弹性绳被拉直后，运动员下降速度减小的阶段，因加速度方向向上，故处于超重状态。
3．45 N
提示：加速时 F – mg = ma。将 a = 3.5g、mg = 10 N 代入，解得 F = 45 N。
4．50 m 时手机对手没有压力；5.32 N
提示：当座舱落到离地面50 m的位置时，仍在自由下落，手机处于完全失重的状态，所以会感觉到手机没有对手施加压力。
座舱自由下落的高度为 h1 = 76 m − 28 m = 48 m。制动过程下落的高度为 h2 = 28 m。设运动过程中的最大速度为 v，制动过程的加速度大小为 a，则 2gh1 = v2 = 2ah2。解得 a =
5．方法 1：设重物的质量为 m，电梯加速度大小为 a，以竖直向上为正方向，根据牛顿第二定律，电梯加速上升时 G1 – mg = ma，电梯减速上升时 G2 – mg = m（− a）。联立解得 a =
方法2：a–t 图像如图所示。
发布时间：2019/12/25 下午8:34:27 阅读次数：10365
