第四章 2 实验:探究加速度与力、质量的关系
速度是描述物体运动状态的物理量,加速度是描述速度变化快慢的物理量。因此也可以说,加速度是描述物体运动状态变化快慢的物理量。由前面的学习我们知道,力是改变物体运动状态的原因,质量大的物体运动状态不容易改变。这说明,加速度与力、质量之间必然存在一定的关系。下面我们来探究加速度与力、质量之间的定量关系。
你认为应该如何完成这个探究实验?比如,研究什么物体?如何测量该物体受到的力?如何测量该物体的加速度?怎样分析数据?请说出你的设计思路并和同学们讨论确定实验探究方案。
用图 4.2–1 所示的装置可以完成这个探究实验。将小车置于水平木板上,通过滑轮与槽码相连。小车可以在槽码的牵引下运动。
加速度与力的关系 保持小车质量不变,通过改变槽码的个数改变小车所受的拉力。小车所受的拉力可认为与槽码所受的重力相等。测得不同拉力下小车运动的加速度,分析加速度与拉力的变化情况,找出二者之间的定量关系。
加速度与质量的关系 保持小车所受的拉力不变,通过在小车上增加重物改变小车的质量。测得不同质量的小车在这个拉力下运动的加速度,分析加速度与质量的变化情况,找出二者之间的定量关系。
可证明这两个力只是近似相等,条件是槽码的质量要比小车的质量小很多。
从实验的角度,同时研究某个物理量与另外两个或多个物理量之间的定量关系是非常困难的。面对这样的问题,我们通常采用控制变量的方法进行研究。
本实验需要测量的物理量有三个:物体的质量、物体所受的作用力和物体运动的加速度。
质量的测量 可以用天平测量质量。为了改变小车的质量,可以在小车中增减砝码的数量。
加速度的测量 方法 1 小车做初速度为 0 的匀加速直线运动,则测量小车加速度最直接的办法就是用刻度尺测量小车移动的位移 x,并用秒表测量发生这段位移所用的时间 t,然后由
\(a = \frac{{2x}}{{{t^2}}}\) (1)
计算出加速度 a。
方法 2 将打点计时器的纸带连在小车上,根据纸带上打出的点来测量加速度(参考第一章的实验方法)。
方法 3 在这个实验中也可以不测量加速度的具体数值。这是因为我们探究的是加速度与其他物理量之间的比例关系,因此测量不同情况下物体加速度的比值即可。
如果能做到让两个做初速度为 0 的匀加速直线运动的物体的运动时间 t 相等,那么由(1)式可知,它们的位移之比就等于加速度之比,即
\(\frac{{{x_1}}}{{{x_2}}} = \frac{{{a_1}}}{{{a_2}}}\) (2)
这样,测量加速度就转换成测量位移了。
力的测量 现实中,仅受一个力作用的物体几乎不存在。然而,一个单独的力的作用效果与跟它大小、方向都相同的合力的作用效果是相同的。因此,实验中作用力 F 的含义可以是物体所受的合力。
如何为运动的物体提供一个恒定的合力,如何测出这个合力是本实验的关键,有很多可行的方法。下面参考案例中的方法可供选用,也可以设计其他方法。
在此实验中,通过测力计用手直接给小车施加一个恒力是否可行?
参考案例 1
用阻力补偿法探究加速度与力、质量的关系
实验装置如图 4.2–2 所示。把木板的一侧垫高,以平衡小车受到的阻力。调节木板的倾斜度,使小车在不受牵引时能拖动纸带沿木板匀速运动。将槽码、小车、打点计时器、纸带安装好。通过改变槽码的个数可以成倍地改变小车所受的拉力,与此相对应,处理纸带上打出的点来测量加速度。
保持小车受的拉力不变,通过增减小车中的重物改变小车的质量。处理纸带上打出的点来测量加速度。
参考案例 2
通过位移之比测量加速度之比
将两辆相同的小车放在水平木板上,前端各系一条细线,线的另一端跨过定滑轮各挂一个小盘,盘中可以放不同的重物。把木板一端垫高,采用参考案例 1 的方法补偿阻力的影响。
两小车后端各系一条细线,用一个物体,例如黑板擦,把两条细线同时按压在木板上(图 4.2–3)。抬起黑板擦,两小车同时开始运动,按下黑板擦,两小车同时停下来。用刻度尺测出两小车移动的位移 x1、x2。由于两小车运动时间 t 相同,从它们的位移之比就可以得出加速度之比。
在盘中重物相同的情况下,通过增减小车中的重物改变小车的质量。
调试实验装置进行实验。
加速度与力的关系 设计表格,把测得的同一个小车在不同拉力 F 作用下的加速度 a 填在表 1 中。
| 拉力 F | |||||
| 加速度 a |
加速度与质量的关系 设计表格,把测得的不同质量的小车在相同拉力作用下的加速度 a 填在表 2 中。
| 质量 m | |||||
| 加速度 a |
为了更直观地判断加速度 a 与拉力 F 的定量关系,我们以 a 为纵坐标、F 为横坐标建立直角坐标系。根据各组实验数据在坐标纸上描点。如果这些点在一条过原点的直线附近,说明加速度 a 与拉力 F 成正比。如果不是这样,则需进一步分析。
为了分析加速度 a 与质量 m 的定量关系,我们同样需要建立直角坐标系。经验告诉我们,在相同拉力作用下,质量 m 越大,加速度 a 越小。这可能是“a 与 m 成反比”,但也可能是“a 与 m2 成反比”,甚至是更复杂的关系。我们从最简单的情况入手,检验是否“a 与 m 成反比”。
实验结果如图 4.2–4 所示,我们很难直观看出图线是否为双曲线,如何解决这个问题呢?
如果 a–m 图像是双曲线,a 与 m 成反比,也就是 a 与 \(\frac{1}{m}\) 成正比。作 a –\(\frac{1}{m}\) 图像进行检验(图 4.2–5)。如果检验的结果是过原点的直线,就可以判断加速度 a 与质量 m 是成反比的。
上述探究实验也可以用参考案例 2 进行。
这里我们已经假设加速度与质量成反比;如果当初假设加速度与质量的二次方成反比,最好作哪两个量之间关系的图像?
控制变量
控制变量的方法是指在研究和解决问题的过程中,对影响事物变化规律的独立因素加以人为控制,使其中只有一个因素按照特定的要求发生变化,而其他因素保持不变,以利于寻找事物发展变化的规律的方法。例如,在研究某个物理量 y 与另外两个变量 x1、x2 的关系时,先固定一个变量 x2 不变,研究 y 与另一个变量 x1 之间的定量关系;然后再固定变量 x1 不变,研究 y 与 x2 之间的关系。
本节在探究加速度与力、质量之间的关系时,就采用了控制变量的方法。以后在研究涉及多个变量的规律时,还会用到控制变量的方法,它是科学研究中常用的一种方法。
1.某同学在做“探究加速度与力的关系”和“探究加速度与质量的关系”实验时,把两个实验的数据都记录在表 3 中。数据是按加速度的大小排列的,两个实验的数据混在一起,
而且有两个加速度数据模糊不清(表 3 中空格)。请你把这些数据分拆填入表 4 和表 5 中,如果模糊的加速度数据是正确的,其数值应该是多少?请填在表 3 中。
| F/ N | m/ kg | a/ (m·s−2) |
| 0.29 | 0.86 | 0.34 |
| 0.14 | 0.36 | 0.39 |
| 0.29 | 0.61 | 0.48 |
| 0.19 | 0.36 | 0.53 |
| 0.24 | 0.36 | |
| 0.29 | 0.41 | 0.71 |
| 0.29 | 0.36 | 0.81 |
| 0.29 | 0.31 | |
| 0.34 | 0.36 | 0.94 |
| F/ N | |||||
| a/ (m·s−2) |
| m/ kg | |||||
| a/ (m·s−2) |
2.某同学用图 4.2–2 所示的实验装置探究小车的加速度 a 与质量 m 的关系。所用交变电流的频率为 50 Hz。
(1)图 4.2–6 是他某次实验得到的纸带,两计数点间有四个点未画出,部分实验数据如图所示。求小车的加速度是多少。
(2)保持小车所受的拉力不变,改变小车质量 m,分别测得不同质量时小车加速度 a 的数据如表 6 所示。
请在图 4.2–7 的坐标纸中作出 a–\(\frac{1}{m}\) 图像。根据 a–\(\frac{1}{m}\) 图像可以得到什么实验结论?
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 质量m / kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
| 加速度a / (m·s−2) | 0.618 | 0.557 | 0.482 | 0.403 | 0.317 | 0.235 | 0.152 | 0.086 |
| 质量倒数\(\frac{1}{m}\)/ kg−1 | 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
第 2 节 实验:探究加速度与力、质量的关系
1.教学目标
(1)经历探究加速度与力、质量的关系的设计过程,能够依据要求进行实验设计,学会选择合理的实验方案进行探究实验。
(2)经历用图像处理数据的过程,从图像中发现物理规律,培养学生收集信息、获取证据的能力。
(3)经历实验操作和测量的过程,知道如何平衡摩擦力、减小系统误差等操作方法,体会探究过程的科学性和严谨性,培养与人合作、学会分享的团队精神。
2.教材分析与教学建议
教科书引导学生从牛顿第一定律出发,提出探究加速度与力、质量关系的必要性,并从实验思路设计、物理量的测量、实验过程和数据分析几个方面引导学生完成探究。实验的基本思路对于学生来说并不困难,因此整个教学过程应该更加重视让学生体会探究的实质:鼓励学生提出科学问题;设计更多的实验方案(并不一定全都实施);引导学生解决实验中遇到的问题;尝试用多种方法处理数据,基于实验数据得出结论;以及培养学生对探究过程和结果进行交流、评估、反思的能力。
本节的重点是让学生经历加速度与力、质量关系的探究过程,体会探究的本质,培养学生提出问题、批判性思维、交流和合作等能力。由于学生在此前的学习中经历了多次探究实验掌习,因此在本节教学中应该更加注重探究的开放性,显现科学探究的本质。
本节的难点是从实验数据中分析加速度与力以及加速度与物体质量的关系,从图像中发现物理规律,并通过这种体验提高使用多种方法和手段分析、处理信息的能力。特别是在探究加速度与质量的关系时,用 \(\frac{1}{m}\) 的数据作为横坐标来处理数据对学生来说是第一次,思维跨度较大,将对学生的思维和心理产生深刻的影响,如果学生能准确理解,熟练掌握,对以后的学习就奠定了坚实的基础。
(1)实验思路
教科书直接给出了从加速度与力的关系和加速度与质量的关系进行探究,同时给出了实验装置引导学生进行具体的设计。
在具体教学过程中,可以对学生提出更开放的问题,比如:如何设计自己的实验来探究加速度与力、质量之间的关系?教师可以鼓励学生设计更多的方案,有条件的学校可以创造机会让学生展示、交流,这样有利于激发学生的主观性和创造性。
下面的教学片段展现了如何引导学生设计实验方案,如何在课堂教学中激发学生的探究欲望,同时也提供了一种不同于教科书的案例选择。
教学片段
探究加速度与力、质量关系的实验设计
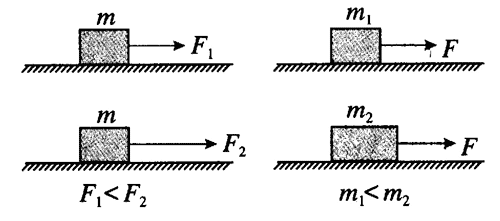
图 4–1
师:如图 4–1 所示,当物体质量一定而受力不相同时,物体的加速度会有什么不同?大小相同的力作用在不同质量的物体上,物体的加速度又会有什么不同?
生:当物体质量一定时,物体的加速度应该随着力的增大而增大,当力大小相同时,物体质量越大,运动状态越难改变,所以质量越大,加速度应该越小。
师:如何把各物理量用精确的数量关系表达出来?
教师引导学生设计实验。
师:为了尽量减小小车与桌面之间摩擦力的影响,请想一想,我们可以用什么样的仪器?
生:可以用气垫导轨来实现减小摩擦…
师:气垫导轨如何减小摩擦?
生:从气孔喷出的气流在导轨与滑块之间形成气垫,从而减小摩擦。
师:为了能较为准确地获得滑块的加速度,要求时间测量误差较小,可以采用数字计时器和光电门作为计时装置。
师:如何给滑块施加恒力呢?
生:可以通过细线悬挂槽码下落的方式给滑块施加恒力。
如果学生能在没有提示的情况下根据实验思路设计实验方案、选用实验装置,这对学生的锻炼和能力的提高会非常有效。但即便学生先知道了使用什么实验器材,教师也应该通过设计适当的问题,引导学生思考实验方案和选用实验装置。
(2)物理量的测量
本实验中有三个需要测量的物理量:a、F、m。质量可以用天平测量,a 与 F 如何测量呢?教师可以把这个较为开放的问题留给学生思考,学生提出不同的实验方案可能会引发出不同的实验装置,但引发学生思考并设计还是很重要的。可以组织学生讨论以下两个问题:
①怎样测量或者比较物体的加速度?
教科书提供了三种不同的方式:一是若小车做初速度为 0 的匀加速直线运动,测量位移 x 和时间 t,由 a = \(\frac{{2x}}{{{t^2}}}\) 计算加速度。二是用打点计时器打出纸带,通过纸带上的计数点求出加速度。三是不直接测量 a 的数值,而是测量不同情况下加速度的比值,并且转化成测量位移的比值。在讨论过程中,学生可能会发现测量物体的加速度有多种不同的方法,可能会提出一些并不容易实现的方案,这些都应该肯定。
②怎样提供并测量施加给小车的恒力?
教科书提供的方法,是利用细线给小车的拉力近似等于槽码的重力,而这种近似要求小车的质量远远大于槽码的质量。为了消除这种系统误差,可以想办法准确测量细线中的实际拉力,比如将力传感器固定在小车上,准确记录细线给小车(含力传感器)的拉力。
以下教学片段采用了传感器来准确测量拉力以消除系统误差,同时可以解决平衡摩擦力的问题。
教学片段
用力传感器探究加速度与力、质量关系的实验设计
在探究加速度与力、质量的关系中,要准确测量施加在物体上的力,可以在物体(小车)上固定一个力传感器,如图 4–2 所示。通过力传感器可以准确记录细线上的拉力,不用再考虑桶的质量要远远小于小车的质量。
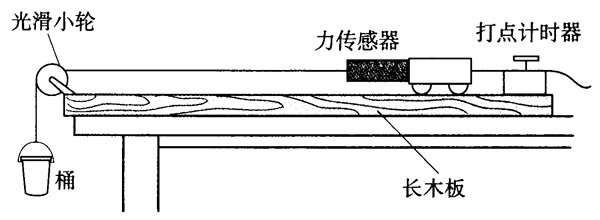
图 4–2
加入力传感器后,要消除摩擦力的影响,可以将装有力传感器的小车放置于水平长木板上,缓慢向桶中加入细沙,直到小车刚开始运动为止,记下传感器的最大示数 F,即为小车所受摩擦力的大小。通过力传感器准确记录小车受到的摩擦力,以便后面平衡摩擦力时用。
(3)进行实验
用打点计时器进行学生分组实验是较为可行的方案。在实验中,教师应该鼓励学生相互合作、积极分享,同时教师应有相应的指导,这些指导中应该包含以下要点:
①平衡摩擦力:用将木板倾斜一定程度进行阻力补偿的方法。开始时不要在小车一端悬挂重物,将打点计时器上的纸带与小车相连,用手给小车一个初速度,让小车在木板上运动。如果在纸带上打出点的间隔是均匀的,表明小车受到的阻力跟它的重力沿斜面向下的分力平衡。
②不重复平衡摩擦力:平衡摩擦力后,不管以后是改变槽码的质量,还是改变小车的质量,都不需要重新平衡摩擦力。
③实验条件:只有当小车的质量远大于槽码的质量时,槽码的重力才可视为小车受到的拉力。
④改变拉力和小车质量后,每次开始时小车应尽量靠近打点计时器,并应先接通电源,后释放小车,且应在小车到达滑轮前按住小车。
⑤设计记录表格,正确记录实验数据。作图时两坐标轴的标度比例要适当,这样作图时坐标点间距不至于过密,误差会小些。
如果选择采用教科书参考案例 2 进行实验,以下教学片段可供参考。
教学片段
通过位移之比测量加速度之比
实验准备:附有滑轮的长木板 2 块;相同的小车 2 个;细线 2 条;槽码多个(10 g、20 g)用于提供牵引小车的力;砝码多个(50 g、100 g、200 g),用于改变小车的质量;刻度尺;1 ~ 2 m 长的适当粗些的棉线两条,用于控制小车的运动;宽口文件夹。
①探究加速度与力的关系:小车质量为 200 g,两车上面均可加 100 g 左右的砝码。保持其中一辆小车所挂槽码不变(如 20 g),另一辆小车所挂槽码质量逐渐加大,但不要过大。
②探究加速度与质量的关系:一辆小车质量固定为 300 g,另一辆小车质量可自 200 g 起,逐渐增加砝码至 700 ~ 800 g。牵引小车的槽码以 30 ~ 40 g 为宜。小车质量过大,会造成夹子夹不住车后的拖线,产生较大的位移误差。
③车后所系线要用适当粗些的棉绳。还可在绳上擦一些松香以增大绳与夹子之间的摩擦力。
④选择口宽、弹力大的夹子。同时为避免夹子开、闭时在桌面上发生移动,最好把夹子固定住。操作夹子时应迅捷有力,且要注意保证小车停止时不能与定滑轮相碰。
⑤描绘 a–F 图像时,横轴用两车拉力之比 \(\frac{{{F_2}}}{{{F_1}}}\),纵轴用对应的两车位移之比 \(\frac{{{x_2}}}{{{x_1}}}\) 表示其加速度之比 \(\frac{{{a_2}}}{{{a_1}}}\);描绘 a–\(\frac{1}{m}\) 图像时,横轴用两车质量之比 \(\frac{{{m_1}}}{{{m_2}}}\),纵轴用对应的两车位移之比 \(\frac{{{x_2}}}{{{x_1}}}\) 表示其加速度之比 \(\frac{{{a_2}}}{{{a_1}}}\)。
(4)数据分析
在数据分析中,教科书详细引导学生思考如何使用图像来获取物理量之间的关系。当两个物理量可能为反比例关系时,需要对一个量取倒数作为新的变量,来寻找所画出的图线是否是直线,从而判断两者是否是正比例或者一次函数的关系。但这一点对学生来说,思维上仍然跨度较大,尤其是想要理解而且形成习惯、灵活运用,更有一定的难度。教师可以通过更多的例子来让学生体会,利用改变纵坐标和横坐标,可以将较为复杂的函数关系用较为简单的图像表示出来。为可能的后续实验(比如单摆测重力加速度)作一些铺垫。
在数据分析中,对基础较好的学生有必要进行误差分析。教师可以对以下两点进行引导和分析:
一是平衡摩擦力不当造成的误差。由于实验原理中要求水平面为光滑水平面,因此在实验中应该平衡摩擦力,如果没有平衡摩擦力或者平衡不当就会带来系统误差。如果学生所画图线中出现了不过原点的情况,那么就可能是平衡摩擦力不当导致的。
二是小车的质量要远远大于槽码的质量。本实验用槽码所受的重力代替细线对小车的拉力,而实际小车所受的拉力 F 要小于槽码所受的重力 m1g。因此,满足槽码的质量 m1 远小于小车的质量 m2 的目的就是为了减小因实验原理不完善而引起的误差。此误差可因 m1 ≪ m2 而减小,但不可能为 0。证明如下:以小车、槽码整体为研究对象得 m1g =(m2 +m1)a,以小车为研究对象得 F = m2a;求得 F = \(\frac{{{m_2}}}{{{m_1} + {m_2}}}\)m1g = \(\frac{1}{{1 + \frac{{{m_1}}}{{{m_2}}}}}\)m1g < m1g。
当然,这些误差的分析和处理可以在学习完牛顿第二定律后进行推导。
3.“练习与应用”参考答案与提示
本节共两道习题。第 1 题练习整理数据,发现规律,形成结论。尝试用得出的实验结论判断实验数据的合理值。第 2 题练习用逐差法、图像法处理实验数据,得出结论。
1.填写教科书中的表 4、表 5 如表 4–1、表 4–2。
表 4–1 探究加速度与力的关系(条件:m = 0.36 kg)
|
F/N |
0.14 |
0.19 |
0.24 |
0.29 |
0.34 |
|
a/(m·s−2) |
0.39 |
0.53 |
0.67 |
0.81 |
0.94 |
表 4–2 探究加速度与质量的关系(条件:F = 0.29 N)
|
m/kg |
0.31 |
0.36 |
0.41 |
0.61 |
0.86 |
|
a/(m·s−2) |
0.94 |
0.81 |
0.71 |
0.48 |
0.34 |
提示:表 4–1 是探究加速度与力的关系,根据质量 m = 0.36 kg 整理数据,发现力 F 等量变化(ΔF = 0.05 N),加速度 a 等量变化(Δa = 0.14 m·s−2),即力与加速度的比值保持 0.36 不变。表 4–2 是探究加速度与质量的关系,根据力 F = 0.29 N 整理数据,发现质量 m 增大,加速度 a 减小,质量和加速度的乘积保持 0.29 不变。
2.(1)0.51 m/s2;(2)如图 4–3 所示可知,加速度与质量成反比。
提示:(1)两计数点间的时间间隔 T = 0.1 s。加速度 a = \(\frac{{({s_4} + {s_3}) - ({s_2} + {s_1})}}{{{{(2T)}^2}}}\) = 0.51 m/s2。
(2)描点,观察点的分布规律,用直线拟合,得到一条过原点的直线,如图4-3所示。根据图像可以得到小车所受的拉力不变时加速度与质量成反比。
发布时间:2019/12/6 下午10:24:31 阅读次数:16367

