第十三章 2 磁感应强度 磁通量
巨大的电磁铁能吸起成吨的钢铁,小磁体却只能吸起几枚铁钉。磁场有强弱之分,那么我们怎样定量地描述磁场的强弱呢?
在研究电场时,我们通过分析检验电荷在电场中的受力情况引入了电场强度这个物理量,用它来描述电场的强弱和方向。我们可以用类似的方法,找出表示磁场强弱和方向的物理量。
用小磁针可以判断空间某点磁场的方向,但很难对它进行进一步的定量分析。若以通电导线作为磁场的检验物体,则既可以知道导线中电流的大小,又能测量导线的长度,从而可以进行定量的研究。
为研究空间某点的磁场,可以考虑在该处放一段很短的通电导线,分析它受到的力。在物理学中,把很短一段通电导线中的电流 I 与导线长度 l 的乘积 Il 叫作电流元。但要使导线中有电流,就要把它接到电源上,所以孤立的电流元是不存在的。如果要研究的那部分磁场的强弱、方向都是一样的,我们也可以用比较长的通电导线进行实验,从结果中推知电流元的受力情况。
探究影响通电导线受力的因素
三块相同的蹄形磁体并排放在桌面上,可以认为磁极间的磁场是均匀的,其强弱与磁体的数目无关。将一根直导线水平悬挂在磁体的两极间,导线的方向与磁场的方向(由下
向上)垂直(图 13.2–1)
有电流通过时,导线将摆动一定角度,通过摆动角度的大小可以比较导线受力的大小。电流的大小可以由外部电路控制,用电流表测量。分别接通“2、3”和“1、4”,可以改变导线通电部分的长度。
分析了很多实验事实后人们认识到,通电导线与磁场方向垂直时,它受力的大小既与导线的长度 l 成正比,又与导线中的电流 I 成正比,即与 I 和 l 的乘积 Il 成正比,用公式表示就是
F = IlB
式中 B 与导线的长度和电流的大小都没有关系。但是,在不同情况下,B 的值是不同的:即使是同样的 I、l,在不同的磁场中,或在非均匀磁场的不同位置,一般说来,导线受的力也是不一样的。看来,B 正是我们要寻找的表征磁场强弱的物理量——磁感应强度(magnetic induction)。由此,在导线与磁场垂直的最简单的情况下(图 13.2–1),有关系式
\[\bbox[5pt,border: 1px solid red]{B = \frac{F}{{Il}}}\]磁感应强度 B 的单位由 F、I 和 l 的单位决定。在国际单位制中,磁感应强度的单位是特斯拉(tesla),简称特,符号是 T,即
1 T = 1 \( \frac{\rm N}{ \rm {A·m}}\)
| 人体器官内的磁场 | 10−13 ~ 10−9 |
| 地磁场在地面附近的平均值 | 5×10−5 |
| 我国研制的作为 α 磁谱仪核心部件的大型 永磁体中心的磁场 |
0.134 6 |
| 电动机或变压器铁芯中的磁场 | 0.8 ~ 1.7 |
| 核磁共振的磁场 | 3 |
| 中子星表面的磁场 | 106 ~ 108 |
| 原子核表面的磁场 | 约1012 |
磁感应强度是矢量,它的方向就是该处小磁针静止时 N 极所指的方向。
如果磁场中各点的磁感应强度的大小相等、方向相同,这个磁场叫作匀强磁场。距离很近的两个平行异名磁极之间的磁场(图 13.2–2),除边缘部分外,可以认为是匀强磁场。
匀强磁场的磁感线用一些间隔相等的平行直线表示。两个平行放置较近的线圈通电时,其中间区域的磁场近似为匀强磁场(图 13.2–3)。这种装置在电子仪器中常常用到。
磁感线的疏密程度表示了磁场的强弱。在图 13.2–4 中,S1 和 S2 两处磁感线的疏密不同,这种不同是如何体现的呢?如果在 S1 和 S2 处,在垂直于纸面方向取同样的面积,穿过相同面积磁感线条数多的就密,磁感应强度就大。
设在磁感应强度为 B 的匀强磁场中,有一个与磁场方向垂直的平面,面积为 S(图 13.2–5),我们把 B 与 S 的乘积叫作穿过这个面积的磁通量(magnetic flux),简称磁通。用字母 Φ 表示磁通量,则
Φ=BS
如果磁感应强度 B 不与我们研究的平面垂直,例如图 13.2–6 中的 S,那么我们用这个面在垂直于磁感应强度 B 的方向的投影面积 Sʹ 与 B 的乘积表示磁通量。
在国际单位制中,磁通量的单位是韦伯(weber),简称韦,符号是 Wb。
1 Wb =1 T·m2
从 Φ = BS 可以得出 B = \(\frac{\Phi }{S}\),这表示磁感应强度的大小等于穿过垂直磁场方向的单位面积的磁通量。
磁通量在今后的学习中有着重要应用。在图13.2-4中,如果 S2 的面积增大,使穿过 S1 的磁感线都穿过 S2,试着在图中画出来,穿过它们的磁通量有什么关系?
指南针与郑和下西洋
磁针能够指向南北,是因为地磁场的存在。指南针的广泛使用,促进了人们对地球磁场的认识。地球的地理两极与地磁两极并不重合(图 13.2–7),因此,磁针并非准确地指南或指北,其间有一个交角,这就是地磁偏角。地磁偏角的数值在地球上的不同地点是不同的。不仅如此,由于地球磁极的缓慢移动,地磁偏角也在缓慢变化。在使用指南针确定南北方向时,只有将地磁偏角考虑在内,才能得出准确的结果。地磁偏角的发现,对于科学的发展和指南针在航海中的应用都很重要。
我国是最早在航海中使用指南针的国家。郑和下西洋的船队已经装备了罗盘,导航时兼用罗盘和观星,二者互相补充、互相修正。他的航海图叫作“针图”,图中的航线叫作“针路”。明清时期,我国海道针经一类书籍相当丰富。
从 1405 年到 1433 年,郑和先后 7 次下西洋,向南到达爪哇,向西到达波斯湾和红海的麦加,最远到达赤道以南的非洲东海岸。郑和下西洋产生的影响是多方面的。它开拓了我国在南洋群岛、印度洋沿岸国家的海外市场,刺激了我国的商品生产,对当时我国资本主义因素的增长有一定的推动作用。它还开辟了从中国到红海、非洲东海岸的航道,绘制了航海地图,总结了当时的航海技术和航海地理知识,对沟通东西方海路交通作出了重大贡献。郑和的航海图连同船队其他人的著作,介绍了他们经过的国家的山川地貌和风土人情,大大开阔了中国人的地理视野。郑和的航海活动不但是中国海上探险事业的巨大成就,也是世界地理发展史上的光辉记录。
1.有人根据 B = \(\frac{F}{Il}\) 提出:磁场中某点的磁感应强度B与通电导线在磁场中所受的磁场力 F 成正比,与电流 I 和导线长度 l 的乘积成反比。这种说法有什么问题?
2.在匀强磁场中,一根长 0.4 m 的通电导线中的电流为 20 A,这条导线与磁场方向垂直时,所受的磁场力为 0.015 N,求磁感应强度的大小。
3.如图 13.2–8,匀强磁场的磁感应强度 B 为 0.2 T,方向沿 x 轴的正方向,且线段 MN、DC 相等,长度为 0.4 m,线段 NC、EF、MD、NE、CF 相等,长度为 0.3 m,通过面积 SMNCD、SNEFC、SMEFD 的磁通量 Φ1、Φ2、Φ3 各是多少?
4.在磁场中放置一条直导线,导线的方向与磁场方向垂直。先后在导线中通入不同的电流,导线所受的力也不一样。图 13.2–9 中的图像表现的是导线受力的大小 F 与通过导线的电流 I 的关系。A、B 各代表一组 F、I 的数据。在甲、乙、丙、丁四幅图中,正确的是哪一幅或哪几幅?说明道理。
第 2 节 磁感应强度 磁通量 教学建议
1.教学目标
(1)在实验基础上,类比电场强度,定义描述磁场强弱和方向的物理量——磁感应强度,并进一步体会微元法和利用物理量之比定义物理量的方法。
(2)知道磁感应强度的定义,知道其方向、大小、定义式和单位。会用磁感应强度的定义式进行有关计算。
(3)知道匀强磁场的特点。
(4)知道磁通量,会计算在匀强磁场中通过某一面积的磁通量。
(5)了解中国古代在指南针使用方面的情况,激发学生的民族自豪感。
2.教材分析与教学建议
本节内容包括磁感应强度和磁通量两部分。磁感应强度是电磁学的基本概念之一,是本章的重点。由于前一节已经学习一些磁场的知识,可以继续将磁场和电场进行类比,启发学生回忆电场强度的定义方法,形成磁感应强度的概念。教科书用小磁针 N 极受力的方向定义磁感应强度的方向,用电流元所受磁场力与电流元之比定义磁感应强度,符合中学生的认知水平。教师要进一步渗透引入探测物描述“场”性质的方法。磁通量是学习电磁感应的基础,比较抽象,学生理解其物理意义比较困难,随着后续知识的学习会有一个循序渐进的理解过程。
本节涉及的科学研究方法有用物理量之比定义新物理量、理想化模型、微元法、类比法。特别需要指出的是,类比法是一种重要的研究方法和思维方法,可以发展学生的求同思维和变异思维能力。
本节的教学重点是磁感应强度概念的建立,理解磁感应强度的物理意义。通过研究问题和情境,在一定条件下对客观事物进行抽象和概括,找出事物的本质特征和共同属性,构建物理模型和概念。
本节的一个教学难点是寻找描述磁场强弱和方向的物理量。另一个难点是对磁通量的物理意义的理解,这是一个循序渐进的过程,不必急于求成。
(1)问题引入
本节引入新课的问题是如何定量地描述磁场强弱。通过提出这样的问题,引导学生形成一种探索的意识。在教学中,建议通过回顾上节课的内容提出问题:磁体周围的磁场有强有弱,那么是否可以利用小磁针在磁场中不同位置的受力大小来描述磁场的强弱呢?
教科书提出通过研究电场中检验电荷的受力情况引入了电场强度这个物理量,自然地引出“是否可以分析磁体或通电导线在磁场中的受力情况,找出表示磁场强弱和方向的物理量”的设问。根据电场中用“电场强度”可以定量地描述电场的强弱,学生可能直接想到用“磁场强度”定量地描述磁场的强弱。如果有学生问到,教师可以说明磁场强度已用来表示另外一个描述磁场的物理量了。
(2)磁感应强度
学生容易接受对磁感应强度方向的规定,即小磁针静止时 N 极所指的方向,但对于磁场中小磁针两极受力的方向,可能仍习惯于用“同名磁极相互排斥,异名磁极相互吸引”来判断。教师应加强引导,使学生注意从场的角度判断小磁针受力的方向,进一步强化“小磁针 N 极受力的方向与磁感应强度的方向相同”的观点。
教科书指出,用小磁针可以判断空间某点磁场的方向,但是难以定量分析。教师要引导学生发散思维,进而提出以通电导线作为磁场的检验物体。这样既可以知道导线中电流的大小,还能测量导线的长度,从而有利于进行定量研究。
教学片段
磁感应强度的定义
教师活动:引导学生思考如何研究和定义电场的强弱,渗透建立描述“场”性质的科学方法——引入探测物。
学生活动:说出在电场中引入检骏电荷,根据检验电荷的受力情况研究电场的强弱,将检验电荷在电场中某个位置所受的力与检验电荷的电荷量之比定义为电场强度。
教师活动:引导学生类比,提出问题:如何定量研究磁场强弱呢?
学生活动:深入思考、自由讨论,提出研究空间某点的磁场强弱时,可以在该处放磁体或者通电导线,分析受力情况。
教师活动:充分肯定学生的设想,并引导学生分析这两种方法的利弊,选择其中更易于定量研究的探测物——通电导线。然后指出在物理学中,把很短的一段通电导线中的电流 I 与导线长度 Δl 的乘积 Il 叫作电流元。引导学生思考为什么要求很短的导线,电流元的含义是什么。
学生活动:列举质点、点电荷等学过的理想化模型,指出电流元也是一种理想化模型,很短、很小就是为了使电流本身对所处磁场影响不大。
教师活动:引导学生设计方案,利用电流探测磁场的强弱。
学生活动:设计实验方案,将通电导线按平行于磁场、垂直于磁场和不平行也不垂直三种方式放置在磁场中,观察受力,从而定性地得到电流方向垂直于磁场时受力最大。
教师活动:引导学生利用控制变量法,设计方案定量研究通电导线受力与导线的长度、电流大小的关系。
通过实验归纳出 \(\frac{F}{Il}\) 是磁场中各点的位置函数,即在磁场中某一确定位置处,无论怎样改变 I 和 l,F 都随 Il 成比例地变化,\(\frac{F}{Il}\) 跟 Il 大小无关,\(\frac{F}{Il}\) 的大小反映了各不同位置处磁场的强弱程度,所以用它来定义磁场的磁感应强度 B。
应对比磁场与静电场,总结磁感应强度的引入和电场强度引入的异同。两者都用物理量之比定义,其基础是力与电荷量、电流元成正比,比值是对应场中各点的位置函数,反映场的强弱。但两者也有明显的不同之处。从方向上看,静电力方向与电场强度方向总是相同或相反的,而磁场力方向与磁感应强度方向总是垂直的;从大小上看,某试探电荷在电场中某位置所受静电力大小是一定的,但某电流元在磁场中某位置所受磁场力大小还与电流方向有关,定义式中的 F 是指电流元受力的最大值。
还应说明 F 是指通电导线电流方向跟所在处磁场方向垂直时的磁场力,此时通电导线受到的磁场力最大。有的学生往往单纯从数学角度出发,由公式 B = \(\frac{F}{Il}\) 得出磁场中某点的 B 与 F 成正比,与 Il 成反比的错误结论。应强调说明,对于确定的磁场中某一位置来说,B 并不因探测电流和导线长度的改变而改变,而是由磁场自身决定的。
本节教学中应做好演示实验,利用现有器材认真设计和改进实验装置,力求良好的实验效果。下面给出探究通电导线在磁场中受力大小与电流定量关系的方案。
用两根约 80 cm 的铜丝将约 15 cm 的铜棒(因铁棒能被磁铁吸引,故不用铁棒)悬挂起来,并将铜丝固定于绝缘木条的接线柱上,然后将木条架在铁架台上。将 0 ~ 10 Ω 的变阻器、量程为 0 ~ 0.6 A 的电流表、学生电源和固定铜丝的接线柱连接起来,铜棒置于一块 U 形磁铁内(内置钕铁硼,磁性较强),在靠近 U 形磁铁的边缘处水平固定一个毫米刻度标尺,铜棒上用纸片做指针。没通电时指针指示标尺的零刻度,逐渐加大电流,记录指针所指示的铜棒的偏移量。实验能得到很好的正比数据,可以反映通电导线在磁场中受力大小与电流大小的正比定量关系。
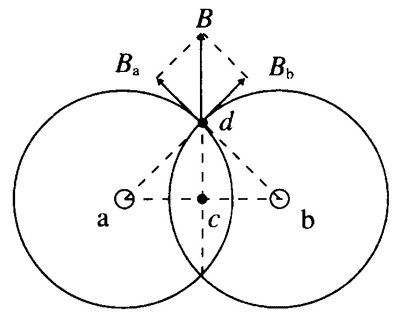
教师还应指出磁感应强度和电场强度一样都是矢量,若空间存在多个磁场,磁场的叠加遵循平行四边形定则。如图 13–7 所示,a、b 是两根通有大小相等、方向相反电流的直导线,可以引导学生画出它们中垂线上 d 点的磁感应强度 B 的大小和方向。
(3)匀强磁场
教科书提出了匀强磁场的概念,要让学生明确几种情形的匀强磁场:距离很近的两个异名磁极之间除边缘部分以外的磁场可看作匀强磁场;通电螺线管内部的磁场近似为匀强磁场;相隔一定距离的两个平行线圈(亥姆霍兹线圈)通电时,其中间区域的磁场近似为匀强磁场。有条件的情况下可以展示亥姆霍兹线圈,也可以演示线圈内的磁感应强度与线圈中的电流成正比,为后面洛伦兹力演示仪的学习搭个台阶。在教学中,可似采用如下片段。
教学片段
探究匀强磁场的特点
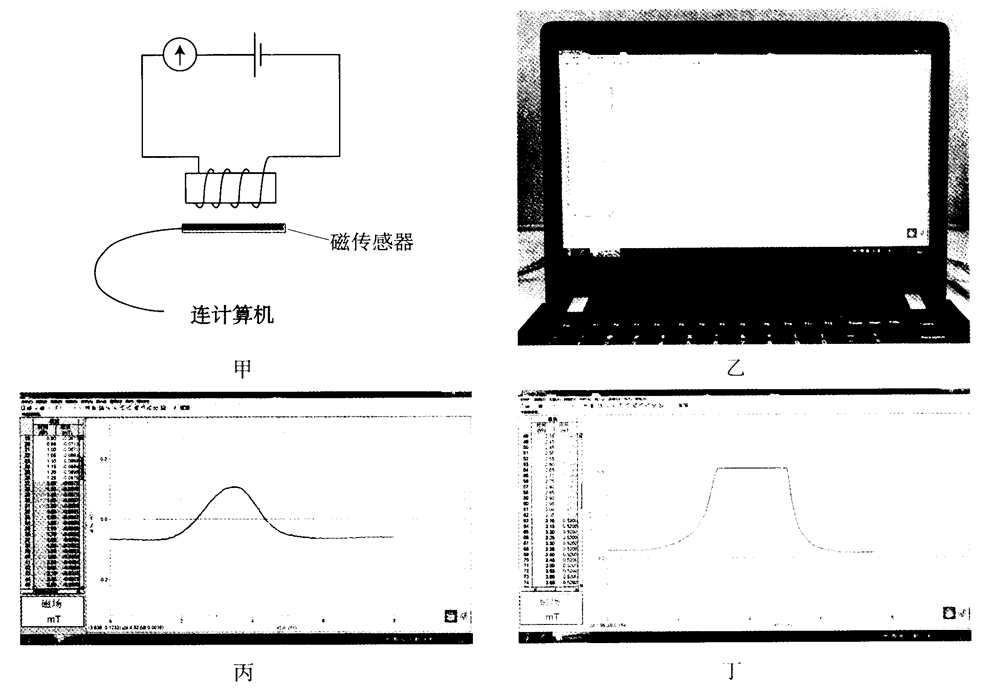
教师活动:用传感器研究磁场。先将磁传感器探头沿南北方向放置测地磁场,示数约为 0.05 mT,再将磁传感器探头反方向放置测地磁场,示数为负值,从而让学生对地磁场的磁感应强度有一定的感性认识。
学生活动:沿不同方向测定地磁场的磁感应强度,定量感受地磁场在什么方向上磁感应强度最强。再测定条形磁体、蹄形磁体的各个部位的磁感应强度。
教师活动:如图 13–8 甲所示,用传感器研究通电螺线管外部的磁感应强度,手持传感器沿着平行于螺线管的一条直线匀速移动。
学生活动:观察、分析计算机中的图像(图 13–8乙、丙),尝试将图像与空间中实际的磁感应强度沿移动直线方向的分量对应。
教师活动:将电源的正、负极对调,重复上述实验,观察图像的变化,再用传感器研究通电螺线管内部的磁感应强度,手持传感器在螺线管内部轴线上匀速移动。
学生活动:观察图像(图 13–8丁),分析得出通电螺线管内部的磁场是恒定。
教师活动:将通电螺线管内部这段恒定的磁场称为匀强磁场。明确指出,匀强磁场是强弱、方向处处相同的磁场。
(4)磁通量
磁通量的概念比较抽象,中学生理解其物理意义比较闲难。磁通量是学习电磁感应的基础,是非常重要的基本概念。教学中应该指出,磁感应强度描述空间场中某一点磁场的强弱和方向。在同一幅图中,磁场越强,磁感线越密,磁感应强度越大。一方面,在研究电磁感应现象时,需要了解穿过某一面积的磁感线的多少和它的变化情况;另一方面,在垂直于磁场方向,穿过相同面积的磁感线条数越多,说明磁场越强。基于以上两点,引入了磁通量的物理概念。
教学片段
定义磁通量概念
教师活动:用手电筒向学生展示一束发散光,再将光束垂直照射在自纸上,前后移动白纸,改变手电筒与白纸之间的距离。
学生活动:认真观察,能看出距离不同时,光打在白纸相同面积上的能量强弱不同。
教师活动:展示光路图,引导学生分析光线的疏密程度表示光能量的强弱。
学生活动:分析图 13–9 甲,能得出当所选面积相同(S1 = S2)而光线疏密程度不同时,通过这一面积的光能量强弱不同。再分析图 13–9 乙,能得出光线疏密程度和所选面积均不同(S1 < S2)时,光能量强弱也可以相同。
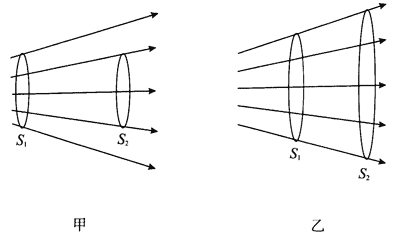
教师活动:引导学生类比。磁感线的疏密程度表示磁场强弱,如果上述光路图是磁感线分布图,可以看到:图 13–9 甲中磁感应强度不同而面积相同的情况下,磁感线条数不同;图 13–9 乙中磁感应强度不同且面积也不同的情况下,穿过的磁感线条数相同。研究电磁感应现象时,我们需要了解穿过某一面积的磁感线的多少和它的变化情况,为此引入磁通量的物理概念。
对磁通量表达式的教学,可以根据对磁通量物理意义的理解,由特殊到一般逐步提高。先研究匀强磁场中与 B 垂直的平面,得到表达式 Φ = BS;再研究匀强磁场中与 B 不垂直的平面,明确这种情况下式中 S 为垂直磁场方向的投影面积。对于基础比较好的学生,还可以指出对于非匀强磁场,可以先把它分成许多可以看成匀强磁场的小区域,再求每一个小区域磁通量的代数和。这也渗透着微元法和累积求和的思想。
教科书直接给出在国际单位制中,磁通量的单位是韦伯。并且指出,从 Φ = BS 可以得出 B = \(\frac{\Phi }{S}\),这表示磁感应强度等于穿过垂直磁场方向的单位面积的磁通量(磁感应强度又叫磁通密度)。教师需要让学生明确磁通量是标量,但有正、负之分。磁感线从一个面的正面穿过和反面穿过时,磁通量的符号是不同的,规定一个面为正值,另一个面就为负值。分析磁通量变化的问题应在“电磁感应”一章中涉及,本节不必过多讨论。
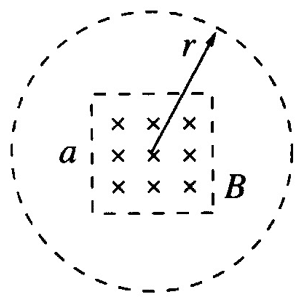
在教学中,教师要指出另外两种特殊情况,学生需要理解特殊情况下计算磁通量的方法。一是当磁场区域小于线圈所围面积时,如图 13–10 所示,应该用有效面积来计算磁通量。二是当穿过所给面积有两个方向的磁场时,如图 13–11 所示,给条形磁体外部套一个圆环,圆环内部就有两个方向的磁场。规定某方向为正,那么相应的磁通量为正值,相反方向的磁场则为负方向,相应的磁通量为负值,总磁通量为各方向磁通量的代数和。
3.“练习与应用”参考答案与提示
本节的第 1、2、3 题都是围绕磁感应强度大小的定义式展开的,第 4 题涉及磁通量的计算。第 1 题是为了纠正学生中常见的一种错误理解,强化对于定义式和决定式的理解。第 2 题利用磁感应强度的定义式进行简单计算。第 3 题给出立体图,要求计算磁通量。需要学生看懂三维坐标图,有一定的空间思维能力。第 4 题通过图像反映物理量之间的关系,强调安培力与电流的正比关系是用物理量之比定义磁感应强度大小的基础。
1.磁感应强度是反映磁场本身强弱和方向的物理量,由磁场本身决定,其大小和方向是确定的,与通电导线以及导线受到的安培力大小无关。
2.1.875×10−3 T
提示:由磁感应强度的定义式,得 B = \(\frac{F}{Il}\) = \(\frac{{0.015}}{{20 \times 0.4}}\) T = 1.875×10−3 T。
3.0.024 Wb,0,0.024 Wb
提示:面积 SMNCD 磁场方向垂直,故磁通量中 Φ1 = BSMNCD = 0.2×0.4×0.3 Wb = 0.024 Wb。面积 SNEFC 与磁场方向平行,故磁通量 Φ2 = 0。面积 SMEFD 与磁场方向的夹角未知,可将其投影到与 x 轴垂直的 MNCD 上。MEFD 的有效面积等于 MNCD 的面积,故磁通量 Φ3 = BSMNCD = 0.2×0.4×0.3 Wb = 0.024 Wb。
4.同一导线通入不同的电流先后放在磁场中的同一位置,并且电流方向都与磁场方向垂直,导线所在处的磁感应强度是确定的。由于 B = \(\frac{F}{Il}\),则 F = BIl。当 B、l 一定时,F – I 图像应是过原点的一条直线,故图乙、丙正确。
发布时间:2019/11/9 下午8:38:23 阅读次数:7197
