第三章 5 共点力的平衡

问题

图甲、乙、丙、丁分别画出了重力为G的木棒在力F₁和F₂的共同作用下处于平衡状态的情况，这些力都位于同一平面内。根据每幅图中各个力作用线的几何关系，可以把上述四种情况的受力分成两类，你认为哪些情况属于同一类？你是根据什么来划分的？

由“问题”栏目中的图示可以看出，图甲和图丁中木棒所受的力是共点力。图乙和图丙中木棒所受的力不是共点力。下面我们来研究物体受共点力平衡的情况。

共点力平衡的条件

物体受到几个力作用时，如果保持静止或匀速直线运动状态，我们就说这个物体处于平衡状态。桌上的书、屋顶的灯、随传送带匀速运送的物体、沿直线公路匀速前进的汽车，都处于平衡状态。

想一想，受共点力作用的物体，在什么条件下才能保持平衡呢？

作用在同一物体上的两个力，如果大小相等、方向相反，并且在同一条直线上，这两个力平衡。二力平衡时物体所受的合力为0。

如果物体受到多个共点力作用，我们可以逐步通过力的合成，最终等效为两个力的作用。如果这两个力的合力为0，则意味着所有力的合力等于0，物体将处于平衡状态。因此，在共点力作用下物体平衡的条件是合力为0，我们把它称为共点力平衡的条件。

【例题1】

某幼儿园要在空地上做一个滑梯（图3.5-1甲），根据空地的大小，滑梯的水平跨度确定为 6 m。设计时，滑板和儿童裤料之间的动摩擦因数取 0.4，为使儿童在滑梯游戏时能在滑板上滑下，滑梯至少要多高？

分析 将滑梯抽象为一个斜面的模型（图3.5-1乙），以正在匀速滑下的小孩为研究对象。

小孩受到三个力的作用：重力 G、斜面的支持力 F_N 和滑动摩擦力 F_f。

当这三个力的合力为 0 时，小孩能在滑板上获得一定速度后匀速滑下，则斜面的高度即为所要求的滑梯的高度。

解 在图 3.5-1 中，沿平行和垂直于斜面两个方向建立直角坐标系。把重力 G 沿两坐标轴方向分解为 F₁ 和 F₂，这样的分解称为正交分解。

设斜面倾角为 θ，由于 F₂ 垂直于 AB、G 垂直于 AC，故 F₂ 和 G 的夹角也等于 θ。用 l、b 和 h 分别表示 AB、AC 和 BC 的长度。

根据共点力平衡的条件和直角三角形中三角函数关系可知：

在 x 轴方向上

F₁ － F_f ＝ 0

F_f ＝ F₁ ＝ Gsinθ ＝ G \(\frac{h}{l}\)        （1）

在y轴方向上

F₂ － F_N ＝ 0

F_N ＝ F₂ ＝ Gcosθ ＝ G\(\frac{}{l}\)         （2）

由于  F_f ＝ μF_N            （3）

把（1）（2）式代入（3）式有

G\(\frac{h}{l}\) = µG\(\frac{b}{l}\)

可求得

h ＝ µb ＝ 0.4×6 m ＝ 2.4 m

滑梯至少要 2.4 m 高，儿童才能从滑梯上滑下。

【例题2】

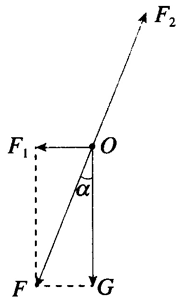
生活中常用一根水平绳拉着悬吊重物的绳索来改变或固定悬吊物的位置。如图 3.5-2，悬吊重物的细绳，其 O 点被一水平绳 BO 牵引，使悬绳 AO 段和竖直方向成θ角。若悬吊物所受的重力为 G，则悬绳 AO 和水平绳 BO 所受的拉力各等于多少？

分析 选取两根绳索连接的 O 点为研究对象，它受到三个力的作用：绳 AO 对它的拉力 F₁、绳 BO 对它的拉力 F₂ 和 O 点下方悬绳对它的拉力 F₃（图3.5-3）。

在平衡状态下，O点所受三个力的合力为0。由于F₃的大小与悬挂物所受的重力相等，且三个力的方向均已知，由此可以求出F₁、F₂的大小。

解 方法1 用两个力的合力和第三个力平衡的方法求解。

如图3.5-3，F₄为F₁和F₂的合力，则F₄与F₃平衡，即

F₄＝F₃＝G

由图可知，F₁＝\(\frac{{{F_4}}}{{\cos \theta }}\)＝\(\frac{G}{{\cos \theta }}\)，F₂＝F₄tanθ，则

F₂＝Gtanθ

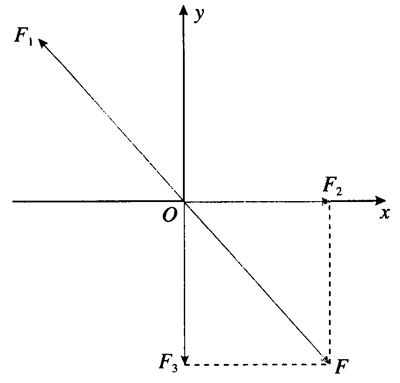
方法2 用正交分解的方法求解。

如图3.5-4，以O为原点建立直角坐标系。F₂方向为x轴正方向，向上为y轴正方向。F₁在两坐标轴方向的分矢量分别为F_1x和F_1y。因x、y两方向的合力都等于0，可列方程

F₂－F_1x＝0

F_1y－F₃＝0

即

F₂－F₁sinθ＝0       （1）

F₁cosθ－G＝0       （2）

由（1）（2）式解得F₁＝\(\frac{G}{{\cos \theta }}\)，F₂＝Gtanθ。

即绳AO和绳BO所受的拉力大小分别为\(\frac{G}{{\cos \theta }}\)和Gtanθ。

练习与应用

本节共5道习题。是模型建构、科学推理、科学论证和质疑创新等科学思维的内化。第1题是一个抽象的共点力平衡问题，可以使学生很好地理解多个共点力的平衡与二力平衡本质上的一致性。其余4题练习运用共点力平衡的知识分析解决实际问题。

1．如图 3.5-5，物体在五个共点力的作用下保持平衡。如果撤去力 F₁，而保持其余四个力不变，请在图上画出这四个力的合力的大小和方向。

参考解答：合力 F 如图所示。

提示：物体在五个力作用下保持平衡，它们的合力为 0。其中任意四个力的合力一定与第五个力大小相等、方向相反。依题意，除 F₁ 以外的四个力的合力，与 F₁ 大小相等、方向相反。撤去 F₁，其余四个力不变，则它们的合力大小等于 F₁，方向与 F₁ 相反。

2．在光滑墙壁上用网兜把足球挂在 A 点，足球与墙壁的接触点为 B（图3.5-6）。足球的质量为 m，悬绳与墙壁的夹角为 α，网兜的质量不计。求悬绳对足球的拉力和墙壁对足球的支持力。

参考解答：拉力为 \(\frac{G}{{\cos \alpha }}\)，与墙壁夹角为 α；支持力为 G tanα，水平向左。

提示：取足球作为研究对象，由共点力的平衡条件可知，F₁ 和 G 的合力 F 与 F₂ 大小相等、方向相反。从图中力的平行四边形定则可得：墙壁对球的支持力大小 F₁ = G tanα，方向水平向左。悬绳对球的拉力大小 F₂ = \(\frac{G}{{\cos \alpha }}\)，方向与墙壁夹角为 α，斜向右上方。

3．如图3.5-7，物体所受重力为 40 N，用细绳 OC 悬于 O 点，绳 OC 所能承受的最大拉力为 50 N。现用细绳  AB绑住绳 OC 的 A 点，再用缓慢增大的水平力牵引 A 点，当 OA 段刚被拉断时，绳 AB 的拉力为多少？

参考解答：30 N

提示：当物体缓慢运动时，可以认为物体处于平衡状态。本题中物体受到三个共点力的作用处于平衡状态，可以将这三个力平移到同一个三角形中，运用直角三角形知讽求解。选 A 点作为研究对象，OA 绳刚拉断时，受力分析如图所示。所以，F₁ = 50 N、F₃ = 40 N，则 F₂ = \(\sqrt {{{50}^2} - {{40}^2}^{}} \) = 30 N。

4．一个质量为 500 kg 的箱子，在平行于斜面的拉力 F 作用下，沿倾角为 30° 的斜面匀速上滑（图3.5-8）。已知箱子与斜面间的动摩擦因数为0.3，拉力F 是多少？

参考解答：3 723 N

提示：沿平行于斜面向上的方向建立 x 轴，沿垂直于斜面向下的方向建立 y 轴，有 F = mgsin30° + F_f，F_N = mgcos30°。又由 F_f = μF_N，解得 F = mgsin30° + μmgcos30°。代入数据解得 F = 3 723 N。

5．将一个质量为 4 kg 的铅球放在倾角为 45° 的斜面上，并用竖直挡板挡住，铅球处于静止状态（图 3.5-9）。不考虑铅球受到的摩擦力，铅球对挡板的压力和对斜面的压力分别是多少？

参考解答：39.2 N；55.4 N

提示：沿水平向右的方向建立 x 轴，沿竖直向下的方向建立 y 轴。根据牛顿第三定律，铅球对挡板的压力 F₁ 与挡板对铅球的支持力 F₁′ 大小相等，则 F₁ = F₁′ = mgtan45° =39.2 N。

同理，铅球对斜面的压力 F₂ 与斜面对铅球的支持力 F₂′ 大小相等，则 F₂ = F₂′ = \(\frac{{mg}}{{\cos 45^\circ }}\) = 55.4 N。

发布时间：2019/11/8 下午11:47:16  阅读次数：6986