质点动力学

目前为止我们已经根据物理运动学知识创建了一个最基本的物理引擎，只需设置质点的初位置、初速度和加速度，物理引擎就会计算出任意时刻质点的速度和位置。那么物体的加速度是由什么决定的呢？这是由大名鼎鼎的牛顿第二定律揭示的，这在物理上属于动力学。

牛顿第二定律

牛顿第二定律牛顿第二定律的内容为：物体的加速度与所受合外力成正比，与物体的质量成反比，公式为：

\[{\bf{F}} = m{\bf{a}}\]

在二维平面上，此方程可以表示成：

\[\begin{array}{l}{F_x} = m{a_x}\\{F_y} = m{a_y}\end{array}\]

其中Fx表示x方向上的合力，ax表示x方向上的加速度，Fy表示y方向上的合力，ay表示y方向上的加速度，这种处理方法在高中物理中叫做正交分解法，其本质就是将矢量运算分解成同方向上的标量运算。

高中物理的知识告诉我们：力学问题通常有两类，一是根据物体的运动情况求它的受力情况，二是根据物体的受力情况求它的运动情况。对于物理引擎来说，我们关注的就是第二种情况，你只需指定物体所受的力，我们就可以根据牛顿第二定律求出物体的加速度，再根据初始速度和初始位移，通过运动学方程就可以解出物体在任意时刻的速度和位置了。

代码实现

由牛顿第二定律可知，物体的加速度可以表达为：

\[{\bf{a}} = \frac{{\bf{F}}}{m}\]

因此在Body类中，我们就要添加两个属性：力force（默认值为零向量）、质量mass（默认值为1 kg），删除加速度acceleration属性，因为它可以从force/mass中求得，Body类中Integrate方法的代码修改如下：

this.velocity.x += (this.force.x * this._invMass + this.gravity.x) * dt;
this.velocity.y += (this.force.y this._invMass + this.gravity.y) * dt;

从上述代码还可以看出，我们还加了一个属性：质量的倒数invMass，添加一个属性的理由有二个：

1．invMass在模拟一个质量为无穷大的物体常常很有用。有些物体无论施加多大的力都不会移动，这对游戏中那些不会移动的物体是很有用的：例如游戏中的墙和地板不会发生移动。我们无法直接将质量设置为无穷大，但可以将invMass设置为0表示无穷大的质量。

2．计算加速度时并没有使用\({\bf{a}} = \frac{{\bf{F}}}{m}\)，而是使用\({\bf{a}} = {\bf{F}} \cdot \frac{1}{m}\)，这样，当质量为无穷大时加速度为0，这正是我们想要的结果。而且乘法计算比除法更快一点。

还要添加一个公开的ApplyForce方法，对质点施加力的作用，代码很简单，就是设置私有变量force的值。代码如下：

ApplyForce(force: Vec2): void {
    this.force.x += force.x;
    this.force.y += force.y;
}

动量定理

动量定理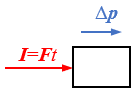在历史上，牛顿对第二定律的原始表述其实更接近于动量定理：物体所受合力的冲量等于物体的动量变化量化量。

两者是等价的，推导过程如下：

\[\begin{array}{l}{\bf{F}} = m{\bf{a}} = m\frac{{{{\bf{v}}_t} - {{\bf{v}}_0}}}{t}\\{\bf{F}}t = m{{\bf{v}}_t} - m{{\bf{v}}_0}\end{array}\]

如果我们将Ft定义为一个新的物理量：冲量I（Impulse）；mv定义为一个新的物理量：动量p（momentum），那么就获得了一个新的物理规律：

\[{\bf{I}} = \Delta {\bf{p}} = m\Delta {\bf{v}}\]

根据这个定律，若物体受到一个冲击力作用时，我们往往无法知道这个冲击力的大小和作用时间，但是可以直接设置一个冲量，就可以求得物体的速度并进一步求出位移，公式如下：

\[{{\bf{v}}_t} = {{\bf{v}}_0} + \frac{{\bf{I}}}{m}\]

在解决碰撞问题时通常都会使用动量定理。

代码实现

添加一个公开的ApplyImpulse方法，可以通过传入的动量改变速度。代码如下：

ApplyImpulse(impulse: Vec2): void {
    this.velocity.x += this._invMass * impulse.x;
    this.velocity.y += this._invMass * impulse.y;
}

空气阻力

空气阻力的物理方程比较复杂，通常可以表达为f=kv2（其中k为一个与空气密度、物体截面积有关的常数），即空气阻力的大小与速度平方成正比，在低速是也可以近似看成f=kv，这样可以减少物理引擎的计算压力，对应的微分方程为：

\[\frac{{d{\bf{v}}}}{{dt}} = - k{\bf{v}},{\bf{v}}\left| {_{t = 0} = {{\bf{v}}_0}} \right.\]

解此方程可得：\(v = {v_0}{e^{ - kt}}\)。

然后进行泰勒级数展开：

\[v = {v_0}(1 - kt + \frac{1}{2}{k^2}{t^2} - \frac{1}{6}{k^3}{t^3} + \ldots )\]

忽略高次项，即在t很小的情况下可以近似认为\(v = {v_0}(1 - kt)\)。

代码实现

非常简单，在Body类中添加一个damping属性，代表上式中的比例系数k。在Integrate方法中添加下面的代码：

this.velocity.SelfMul(1.0 / (1.0 + dt * this.damping));

Body类的完整代码如下：

export class Body {
    position: Vec2 = Vec2.ZERO;
    velocity: Vec2 = Vec2.ZERO;
    gravity: Vec2 = Vec2.ZERO;

    private force: Vec2 = Vec2.ZERO;
    private _mass: number = 1;
    private _invMass: number = 1;
    private _damping: number = 0.1;

    get mass(): number {
        return this._mass
    }
    set mass(value) {
        if (value <= 0) {
            this._mass = 1;
        }
        this._invMass = 1 / this._mass;
    }
    
    get damping(): number {
        return this._damping;
    }
    set damping(value) {
        if (value <= 0) {
            this._damping = 0;
        }
    }

    constructor(world: World) {
        this.gravity = world.gravity;
    }

    ApplyForce(force: Vec2): void {
        this.force.x += force.x;
        this.force.y += force.y;
    }

    ApplyImpulse(impulse: Vec2): void {
        this.velocity.x += this._invMass * impulse.x;
        this.velocity.y += this._invMass * impulse.y;
    }


    Integrate(dt: number) {
        this.velocity.x += (this.force.x * this._invMass + this.gravity.x) * dt;
        this.velocity.y += (this.force.y * this._invMass + this.gravity.y) * dt;
        this.velocity.SelfMul(1.0 - dt * this.damping);  // 空气阻力

        this.position.x += this.velocity.x * dt;
        this.position.y += this.velocity.y * dt;

        this.clearForce();
    }

    private clearForce(): void {
        this.force.x = this.force.y = 0;
    }
}

引擎示例

下面的代码模拟了在空中做平抛运动的物体受到风力影响的运动情况，按数字键0取消风力，按方向键分别模拟上、下、左、右四个不同方向的风力，按i键可以对物体施加一个向上的冲量。

export class test {
    world: World;
    circleBody: Body
    render: Render;

    isPause: boolean = true;

    canvas: HTMLCanvasElement;
    btnStart: HTMLButtonElement;
    btnReset: HTMLButtonElement;

    flag: number = 0;

    public constructor() {

        this.btnStart = <HTMLButtonElement>document.getElementById('btnStart');
        this.btnReset = <HTMLButtonElement>document.getElementById('btnReset');

        this.canvas = <HTMLCanvasElement>document.getElementById('canvas');
        this.render = new Render(this.canvas.getContext("2d"));

        this.btnStart.onclick = () => {
            this.isPause = !this.isPause;
            if (this.isPause) {
                this.btnStart.innerHTML = "开始";
            }
            else {
                this.btnStart.innerHTML = "暂停";
            }
        }
        this.btnReset.onclick = () => {
            this.reset();
        }

        window.onkeyup = (event) => {
            // 监听键盘所触发的事件，同时传递参数event
            switch (event.keyCode) {
                case 48:
                case 96:  // 0
                    this.flag = 0;
                    break;
                case 37:  // 左键
                    this.flag = 1;
                    break;
                case 38:  // 上键
                    this.flag = 2;
                    break;
                case 39:  // 右键
                    this.flag = 3;
                    break;
                case 40:  //下键
                    this.flag = 4;
                    break;
                case 73:  //i 键
                    this.circleBody.ApplyImpulse(new Vec2(0, -200))
                    break;
            }
        }

        this.world = new World();
        this.world.gravity = new Vec2(0, 100);
        this.circleBody = new Body(this.world);
        this.circleBody.position = new Vec2(100, 300);
        this.circleBody.velocity = new Vec2(200, 0);
        this.circleBody.damping = 0;
        this.world.addBody(this.circleBody);

        this.Update();
    }

    private previousTime: number;         // 上一帧的开始时刻
    private elapsedTime: number;          // 每帧流逝的时间（毫秒）

    Update() {

        requestAnimationFrame(() => this.Update());

        const time: number = performance.now();
        this.elapsedTime = this.previousTime ? (time - this.previousTime) / 1000 : 0;
        this.previousTime = time;

        if (this.elapsedTime > 0) {
            if (this.isPause)
                return;

            // 在边界处反弹
            if (this.circleBody.position.x < 20) {
                this.circleBody.position.x = 20;
                this.circleBody.velocity.x = -this.circleBody.velocity.x;
            }
            else if (this.circleBody.position.x > 780) {
                this.circleBody.position.x = 780;
                this.circleBody.velocity.x = -this.circleBody.velocity.x;
            }
            if (this.circleBody.position.y < 20) {
                this.circleBody.position.y = 20;
                this.circleBody.velocity.y = -this.circleBody.velocity.y;
            }
            else if (this.circleBody.position.y > 580) {
                this.circleBody.position.y = 580;
                this.circleBody.velocity.y = -this.circleBody.velocity.y;
            }
            
            // 根据按键施加力或冲量
            switch (this.flag) {
                case 0:  // 数字0
                    this.circleBody.ApplyForce(Vec2.ZERO);
                    break;
                case 1:
                    this.circleBody.ApplyForce(new Vec2(-100, 0))
                    break;
                case 2:  // 上键
                    this.circleBody.ApplyForce(new Vec2(0, -100))
                    break;
                case 3:  // 右键
                    this.circleBody.ApplyForce(new Vec2(100, 0))
                    break;
                case 4:  //下键
                    this.circleBody.ApplyForce(new Vec2(0, 100))
                    break;
            }
            this.world.step(this.elapsedTime);
        };
        this.render.draw(this.world);
    };

    reset(): void {
        this.circleBody.position = new Vec2(100, 300);
        this.circleBody.velocity = new Vec2(200, 0);
        this.btnStart.innerHTML = "开始";
        this.isPause = true;
        this.render.draw(this.world);
    }
}

window.onload = () => {
    var main: test = new test();
}
文件下载（已下载 3 次）

发布时间：2019/8/16 下午10:40:39  阅读次数：3739

2006 - 2025，推荐分辨率 1024*768 以上，推荐浏览器 Chrome、Edge 等现代浏览器，截止 2021 年 12 月 5 日的访问次数：1872 万 9823。 站长邮箱

沪 ICP 备 18037240 号-1，

沪公网安备 31011002002865 号