二维质点运动学
物理知识
上一篇文章只讨论了一维方向上的运动，如果扩展到二维一点也不难，只需在两个维度上进行同样的操作，即：
\[\begin{array}{l}{v_x} = {a_x}dt,{v_y} = {a_y}dt\\x = {v_x}dt,y = {v_y}dt\end{array}\]以上运动学方程也可以写成矢量式：
\[\begin{array}{l}{\bf{v}} = {\bf{a}}dt\\{\bf{r}} = {\bf{v}}dt\end{array}\]这在物理学上叫做运动独立性原理，即：一个物体同时参与几种运动，各分运动都可看成独立进行的，互不影响，物体的合运动则视为几个相互独立分运动叠加的结果。分运动和合运动之间具有：独立性、等时性、矢量性、同体性。
代码实现
与上一个物理引擎相比，代码最主要的变化就是在Body类中：之前物体的位置、速度、加速度都是用一个数字（标量）表示的，现在这些属性用矢量来表示。因此首先编写一个二维矢量类Vec2，代码如下：
export class Vec2 {
static readonly ZERO: Readonly<Vec2> = new Vec2(0, 0);
static readonly UNITX: Readonly<Vec2> = new Vec2(1, 0);
static readonly UNITY: Readonly<Vec2> = new Vec2(0, 1);
x: number = 0;
y: number = 0;
constructor(x: number = 0, y: number = 0) {
this.x = x;
this.y = y;
}
Clone(): Vec2 {
return new Vec2(this.x, this.y);
}
SetZero(): Vec2 {
this.x = 0;
this.y = 0;
return this;
}
Set(x: number, y: number): Vec2 {
this.x = x;
this.y = y;
return this;
}
Copy(other: Vec2): Vec2 {
this.x = other.x;
this.y = other.y;
return this;
}
SelfAdd(v: Vec2): Vec2 {
this.x += v.x;
this.y += v.y;
return this;
}
AddV(v: Vec2): Vec2 {
return new Vec2(this.x + v.x, this.y + v.y);
}
SelfSub(v: Vec2): Vec2 {
this.x -= v.x;
this.y -= v.y;
return this;
}
SubV(v: Vec2): Vec2 {
return new Vec2(this.x - v.x, this.y - v.y);
}
SelfMulS(s: number): Vec2 {
this.x *= s;
this.y *= s;
return this;
}
MulS(s: number): Vec2 {
return new Vec2(this.x * s, this.y * s);
}
Dot(v: Vec2): number {
return this.x * v.x + this.y * v.y;
}
CrossV(v: Vec2): number {
return this.x * v.y - this.y * v.x;
}
Length(): number {
const x: number = this.x, y: number = this.y;
return Math.sqrt(x * x + y * y);
}
LengthSquared(): number {
const x: number = this.x, y: number = this.y;
return (x * x + y * y);
}
Normalize(): Vec2 {
const inv_length: number = 1 / this.Length();
return new Vec2(this.x * inv_length, this.y * inv_length);
}
SelfNormalize(): Vec2 {
const length: number = this.Length();
if (length >= 0.001) {
const inv_length: number = 1 / length;
this.x *= inv_length;
this.y *= inv_length;
}
return this;
}
SelfRotate(radians: number): Vec2 {
const c: number = Math.cos(radians);
const s: number = Math.sin(radians);
const x: number = this.x;
this.x = c * x - s * this.y;
this.y = s * x + c * this.y;
return this;
}
Rotate(radians: number): Vec2 {
const v_x: number = this.x, v_y: number = this.y;
const c: number = Math.cos(radians);
const s: number = Math.sin(radians);
return new Vec2(c * v_x - s * v_y, s * v_x + c * v_y);
}
SelfCrossVS(s: number): Vec2 {
const x: number = this.x;
this.x = s * this.y;
this.y = -s * x;
return this;
}
SelfCrossSV(s: number): Vec2 {
const x: number = this.x;
this.x = -s * this.y;
this.y = s * x;
return this;
}
SelfAbs(): Vec2 {
this.x = Math.abs(this.x);
this.y = Math.abs(this.y);
return this;
}
SelfNeg(): Vec2 {
this.x = (-this.x);
this.y = (-this.y);
return this;
}
Neg(): Vec2 {
return new Vec2(-this.x, -this.y);
}
}
这个类包含了矢量相加（AddV）、相减（SubV）、矢量与标量的乘法（MulS）、矢量间的点乘（Dot）、矢量间的叉乘（Cross）等方法。
有了Vec2类，就可以改写Body类了。代码如下：
export class Body {
position: Vec2 = Vec2.ZERO;
velocity: Vec2 = Vec2.ZERO;
acceleration: Vec2 = Vec2.ZERO;
private world: World;
constructor(world: World) {
this.world = world;
this.acceleration.SelfAdd(world.gravity);
}
Integrate(dt: number) {
this.velocity.x+=this.acceleration.x*dt;
this.velocity.y+=this.acceleration.y*dt;
// 相当于前两行代码
// this.velocity.SelfAdd(this.acceleration.MulS(dt));
this.position.x+=this.velocity.x*dt;
this.position.y+=this.velocity.y*dt;
// 相当于前两行代码
//this.position.SelfAdd(this.velocity.MulS(dt));
}
}
在Body类中还有一个小小的变动：添加了一个重力加速度，而这个加速度是保存在世界中的。这可以理解为，在地球表面，所有物体都具有一个方向竖直向下的重力加速度，默认值为10 m/s2。
应用
下面用物理中几个典型的平面运动来测试一下这个引擎。
1、抛体运动
所谓抛体运动，就是将物体以一定的初速度向空中抛出，仅在重力作用下物体所做的运动。
由于物体默认就自带重力加速度，因此我们只需设置它的初速度即可。代码如下：
export class test {
world: World;
circleBody: Body
render: Render;
canvas: HTMLCanvasElement;
v: number = 200;
alpha: number = 0;
public constructor() {
this.canvas = <HTMLCanvasElement>document.getElementById('canvas');
this.render = new Render(this.canvas.getContext("2d"));
this.world = new World();
// 将重力加速度设置得大一点
this.world.gravity = new Vec2(0,100);
this.circleBody = new Body(this.world);
this.circleBody.position = new Vec2(100, 300);
this.circleBody.velocity = new Vec2(this.v, 0);
this.resetBody();
this.world.addBody(this.circleBody);
this.Update();
}
private previousTime: number; // 上一帧的开始时刻
private elapsedTime: number; // 每帧流逝的时间（毫秒）
Update() {
requestAnimationFrame(() => this.Update());
const time: number = performance.now();
this.elapsedTime = this.previousTime ? (time - this.previousTime) / 1000 : 0;
this.previousTime = time;
if (this.elapsedTime > 0) {
this.world.step(this.elapsedTime);
// 在边界处反弹
if (this.circleBody.position.x < 20) {
this.circleBody.position.x = 20;
this.circleBody.velocity.x = -this.circleBody.velocity.x;
}
else if (this.circleBody.position.x > 780) {
this.circleBody.position.x = 780;
this.circleBody.velocity.x = -this.circleBody.velocity.x;
}
if (this.circleBody.position.y < 20) {
this.circleBody.position.y = 20;
this.circleBody.velocity.y = -this.circleBody.velocity.y;
}
else if (this.circleBody.position.y > 580) {
this.circleBody.position.y = 580;
this.circleBody.velocity.y = -this.circleBody.velocity.y;
}
};
this.render.draw(this.world);
};
}
window.onload = () => {
var main: test = new test();
}
200m/s
0°
2、匀速圆周运动
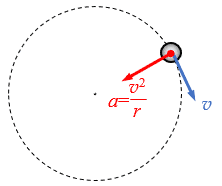匀速圆周运动的加速度a与速度v时刻垂直，且满足如下关系：
\[a = \frac{{{v^2}}}{R}\]
式中R表示圆周半径。因此在代码中需要将v矢量旋转90°，将这个矢量的长度缩放为\(\frac{{{v^2}}}{R}\)的大小，即a矢量。
设做匀速圆周运动的物体速率v=200 m/s，运动半径R=200 m，由物理公式可求得T=\(\frac{{2\pi R}}{v}\)=2π s。下面的代码用来模拟这个运动：
export class test {
world: World;
circleBody: Body
render: Render;
canvas: HTMLCanvasElement;
R: number = 200;
v: number = 200;
public constructor() {
this.canvas = <HTMLCanvasElement>document.getElementById('canvas');
this.render = new Render(this.canvas.getContext("2d"));
this.world = new World();
// 将重力加速度设置为0
this.world.gravity = Vec2.ZERO;
this.circleBody = new Body(this.world);
this.circleBody.position = new Vec2(400, 100);
this.circleBody.velocity = new Vec2(200, 0);
this.world.addBody(this.circleBody);
this.Update();
}
private previousTime: number; // 上一帧的开始时刻
private elapsedTime: number; // 每帧流逝的时间（毫秒）
Update() {
requestAnimationFrame(() => this.Update());
const time: number = performance.now();
this.elapsedTime = this.previousTime ? (time - this.previousTime) / 1000 : 0;
this.previousTime = time;
if (this.elapsedTime > 0) {
var tempV:Vec2=new Vec2();
this.circleBody.acceleration = Vec2.RotateV(this.circleBody.velocity,Math.PI / 2,tempV)
.SelfNormalize().SelfMul(this.v * this.v / this.R);
this.world.step(this.elapsedTime);
};
this.render.draw(this.world);
};
}
window.onload = () => {
var main: test = new test();
}
周期挺准的，但圆弧轨迹不断得缓慢上移，不算完美。
3、单摆
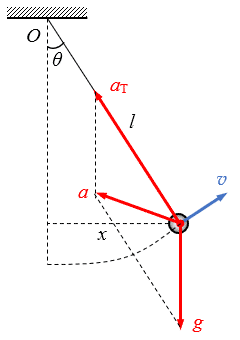单摆的运动比较复杂，摆球的速度沿圆弧切线方向，而其加速度可以这样处理：设摆长为l，摆角为θ，摆球偏离悬点的水平距离为x，则有：
\[\theta = \arcsin \frac{x}{l}\]
由牛顿第二定律可求的摆线的拉力：
\[T = mg\cos \theta + m\frac{{{v^2}}}{l}\]
对应产生的加速度：
\[{a_T} = g\cos \theta + \frac{{{v^2}}}{l}\]
而小球的加速度为aT和g的矢量和。
下面的例子设重力加速度为g=100 m/s2，摆长为l=400 m，将摆球由最低点以v0=200 m/s的初速度释放，由机械能守恒定律可知最大摆角可达到60°，由单摆周期的修正公式：
\[T = 2\pi \sqrt {\frac{l}{g}} (1 + \frac{1}{4}{\sin ^2}\frac{{{\theta _m}}}{2} + \frac{9}{{64}}{\sin ^4}\frac{{{\theta _m}}}{2} + \cdots )\]
可求得周期为13.46 s。
以下代码就用来模拟这个运动并求出周期：
export class test {
world: World;
circleBody: Body
render: Render;
canvas: HTMLCanvasElement;
theta: number = 0;
a_T: number = 0;
readonly l: number = 400;
readonly grivaty: number = 100;
public constructor() {
this.canvas = <HTMLCanvasElement>document.getElementById('canvas');
this.render = new Render(this.canvas.getContext("2d"));
this.world = new World();
this.circleBody = new Body(this.world);
this.circleBody.position = new Vec2(400, 250);
this.circleBody.velocity = new Vec2(200, 0);
this.world.addBody(this.circleBody);
this.Update();
}
private previousTime: number; // 上一帧的开始时刻
private elapsedTime: number; // 每帧流逝的时间（毫秒）
Update() {
requestAnimationFrame(() => this.Update());
const time: number = performance.now();
this.elapsedTime = this.previousTime ? (time - this.previousTime) / 1000 : 0;
this.previousTime = time;
if (this.elapsedTime > 0) {
this.theta = Math.asin((this.circleBody.position.x - 400) / this.l);
this.a_T = this.grivaty * Math.cos(this.theta) +
this.circleBody.velocity.LengthSquared() / this.l;
this.circleBody.acceleration = new Vec2(-this.a_T * Math.sin(this.theta),
this.grivaty - this.a_T * Math.cos(this.theta));
this.world.step(this.elapsedTime);
};
this.render.draw(this.world);
};
}
window.onload = () => {
var main: test = new test();
}
周期求得挺准的，但运动弧线在不断地微微上移，不算完美。
文件下载（已下载 1 次）发布时间：2019/8/14 下午10:56:27 阅读次数：3479
