一维质点运动学

曾经在2011年研究过一阵子物理引擎，但半途而废了。当时用的编程语言是C#，对应平台是已被微软放弃的Silverlight。现在准备重振旗鼓再冲击一次，用的语言是TypeScript，这样就可以在浏览器中使用这个引擎，通用性更好。

物理知识

质点是一个理想化物理模型，无需考虑它的大小形状，在高中物理中大多数情况中都可以把物体看成一个有质量的点，而且点也没有旋转的概念。

运动学是对物体运动的研究，并不考虑物体上的作用力，我们只关心质点的位移、速度和加速度随时间变化的规律。

在初中物理中我们就已经学过匀速直线运动，加速度为0，位移与速度关系为：

\[{x_t} = {x_0} + vt\]

式中xt表示t秒末的位移，x0表示初始位移，v为速度，它是一个有方向的矢量，表征物体运动的快慢，从另一个角度理解，它也是物体单位时间中位移的改变量，例如v＝5m/s向右，即表示物体每秒钟向右移动5 m的距离。

到了高中，我们又学习了匀变速直线运动，此运动中速度与加速度的关系为：

\[{v_t} = {v_0} + at\]

加速度a也是矢量，表示速度变化的快慢，从另一个角度理解，它也是物体单位时间中速度的改变量，例如a＝5 m/s2向右，表示物体的速度每秒钟在向右方向增加5 m/s。

而位移、初速度和加速度之间的关系为：

\[x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\]

那么上面那个公式究竟是如何得出的？高中物理教材使用的都是微积分的思想，如下图所示为人教版的推导示意图。

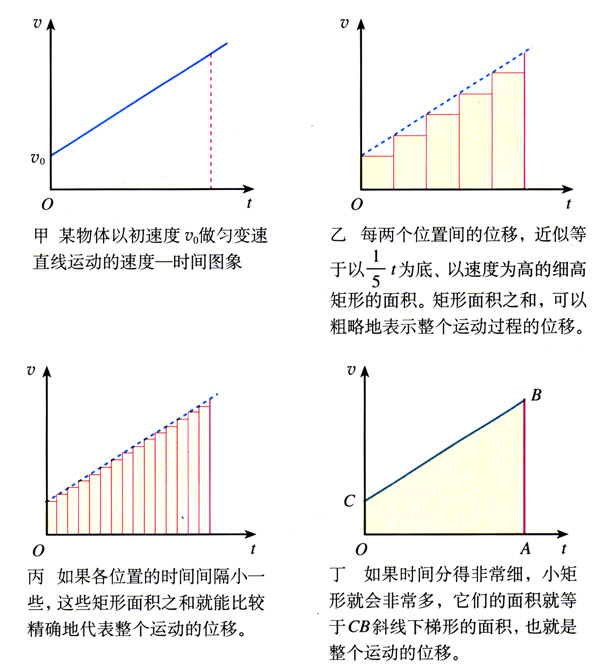
对于上图，不妨对应这么一个匀加速过程：v0=1 m/s，a=2m/s2，求t=1 s时的x。

对应甲图，即得到x的精确解，为2 m。

对应乙图，将1 s分成5个Δt，且Δt=0.2 s。将这五段都看出匀速直线运动，速度为该段的初速度，则物体的位移为这五段匀速运动位移之和。下面的表格显示了计算值和精确值的比较：

步数 t x的计算值 x的精确值 差值

1

0.20

0.2

0.24

0.04

2

0.40

0.48

0.56

0.08

3

0.60

0.84

0.96

0.12

4

0.80

1.28

1.44

0.16

5

1.00

1.8

2

0.2

在这个例子中，计算值比精确值要小，且随着时间的增加，误差越来越大。

那将Δt（在数值分析这门学科中，Δt又叫做步长，用h表示）减小会如何呢？对应丙图，这次取Δt=0.02，相应的表格如下：

步数 t x的计算值 x的精确值 差值

1

0.02

0.02

0.0204

0.0004

…

…

…

…

…

20

0.40

0.552

0.56

0.008

…

…

…

…

…

30

0.60

0.948

0.96

0.012

…

…

…

…

…

40

0.80

1.424

1.44

0.016

…

…

…

…

…

50

1.00

1.98

2

0.02

这次误差小得多，可以想象，若Δt→0，那么计算出的值就应该等于精确值，如图丁所示。

 

在计算机上不可能做到Δt→0，通常网页的刷新频率为1/60s，物理引擎的刷新率设置为1/30s通常就能满足要求了。

总结下来，在电脑上进行运动的仿真计算，需要将时间分割成长度为Δt一小段，将这每一小段都看成匀速直线运动，由xi=viΔt计算出每一小段的位移，最后将这些位移相加即可，伪代码如下：

void Update(dt)
{
    v+=a*dt;
    x+=v*dt;
}

物体的运动情况归根结底是由它的初始状态（初始位移和初速度）和加速度（严格地说，应该是由受力情况决定的，这会在后面的质点动力学中进行讨论）决定的，因此只需设置物体的初始位置、初速度和加速度，计算机程序就会自动算出任意时刻物体的位置了。

实现StunPhysics引擎

理解了背后的物理知识，下面我们就开始实现一个史上最简陋的2D物理引擎，我把它命名为StunPhysics。主要参考了Box2D.ts，matter.js和p2.js。使用的编辑器为Visual Studio Code。

如下图所示，可以把物理引擎对应现实世界的台球桌，即我们的物理世界（World），而台球上的桌球就是处于这个世界的物体（Body），我们只要对物体施加“第一推动”，接下去物理引擎就可以像拉普拉斯魔那样预测出物体的未来。

图1

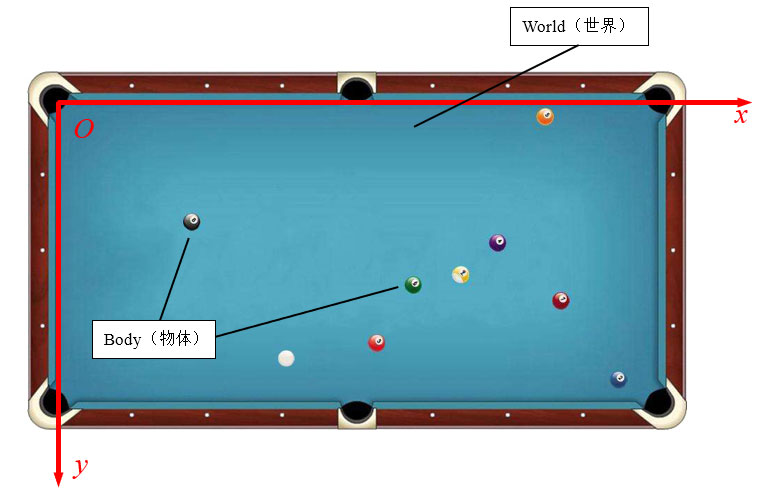
因此首先创建我们的世界——World类，代码如下：

import { Body } from "./objects/Body";

export class World {

    bodies: Array<Body>;

    constructor() {
        this.bodies = new Array<Body>();
    }

    addBody(body: Body) {
        this.bodies.push(body);
    }

    step(dt: number) {
        for (let i: number=0; i < this.bodies.length; i++){        
            this.bodies[i].Integrate(dt);
        }
    }
}

这个类管理一个Body的集合，在它的step方法中更新集合中所有Body的速度和位移。

Body类表示一个物体，目前表示一个质点。这个类保存了物体的位置、速度和加速度。最关键的代码位于积分运算的Integrate方法中：

import { World } from "../World";

export class Body {
    x: number = 0;
    velocity: number = 0;
    acceleration: number = 0;

    Integrate(dt: number) {
        this.velocity += this.acceleration * dt;
        this.x += this.velocity * dt;
    }

好了，至此，史上最简陋的物理引擎制作完毕，物理引擎就相当于一个黑箱，输入初位置、初速度，目前还需要输入加速度，它就可以计算出下一帧的新状态，如下图所示：

图2

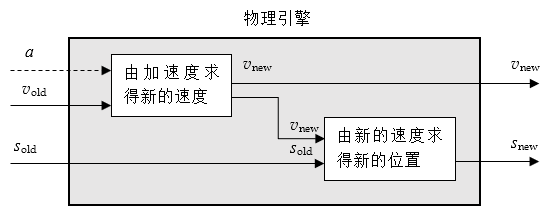
最后为了调试方便，还添加了一个绘图类Render（对物理引擎来说它不是必须的），它可以在屏幕上绘制圆形代表Body。代码如下：

import { World } from "../World";
import { Body } from "../objects/Body";

export class Render {
    ctx: CanvasRenderingContext2D;

    constructor(ctx: CanvasRenderingContext2D) {
        this.ctx = ctx;
    }

    draw(world: World) {
        this.ctx.clearRect(0, 0, this.ctx.canvas.width, this.ctx.canvas.height);
        this.ctx.save();

        for (let i: number=0; i < world.bodies.length; i++) {
            const body: Body = world.bodies[i];
            this.drawSolidCircle(body.x, 40, 20);            
        }

        this.ctx.restore();
    }

    private drawSolidCircle(x: number, y: number, radius: number) {
        const ctx: CanvasRenderingContext2D = this.ctx;
        if (ctx) {
            const cx: number = x;
            const cy: number = y;
            ctx.beginPath();
            ctx.arc(cx, cy, radius, 0, Math.PI * 2, true);
            ctx.moveTo(cx, cy);
            ctx.lineTo((cx + radius), cy);
            ctx.fillStyle = "rgba(255,0,0,0.5)";
            ctx.fill();
            ctx.strokeStyle = "rgb(255,0,0)";
            ctx.stroke();
        }
    };
}

应用

下面我们使用这个引擎模拟一下几个常见的物理情境。

1、匀变速直线运动

根据物理知识，首先需要设定物体的初始条件：x0、v0，在下面的例子中，小球被放置在画布偏左侧，坐标值为100 m（以1个像素为1 m），初速度设置为25 m/s，匀变速直线运动的加速度是个恒量，可以设置为25 m/s2。

现在可以算一下小球位移600 m所需的时间，由运动学公式：

\[x =  {v_0}t + \frac{1}{2}a{t^2}\]

可求得可求得t=6 s。

下面用物理引擎来计算一下这个时间，代码如下：

import { Render } from "../../src/render/Render";
import { World } from "../../src/World";
import { Body } from "../../src/objects/Body";

export class test {
    world: World;
    circleBody: Body
    render: Render;
    canvas: HTMLCanvasElement;

    public constructor() {
        this.canvas = <HTMLCanvasElement>document.getElementById('canvas');
        this.render = new Render(this.canvas.getContext("2d"));
        // 初始化物理引擎
        this.world = new World();
        // 初始化物体，并设置它的位置、速度和加速度
        this.circleBody = new Body();
        this.circleBody.x = 100;
        this.circleBody.velocity = 25;
        this.circleBody.acceleration = 25;
        this.world.addBody(this.circleBody);

        this.Update();
    }

    private previousTime: number;         // 上一帧的开始时刻
    private elapsedTime: number;          // 每帧流逝的时间（毫秒）
    private totalTime: number = 0;        // 程序运行的总时间

    Update() {
        requestAnimationFrame(() => this.Update());

        const time: number = performance.now();
        this.elapsedTime = this.previousTime ? (time - this.previousTime) / 1000 : 0;
        this.previousTime = time;

        if (this.circleBody.x > 700) {
            return;
        }

        if (this.elapsedTime > 0) {
            this.world.step(this.elapsedTime);
        };
        this.render.draw(this.world);
    };
}

window.onload = () => {
    var main: test = new test();
    main.start();
}

程序界面如下（由于又增加了一些UI控件，因此其背后的代码比上面的要复杂，详细的代码可参见文章底部的链接）：

2、简谐振动谐

首先还是需要设定初始条件x0、v0，这次将小球放置在画布中央，坐标值为400 m，初速度设置为200 m/s。

简谐振动应满足：F回=-kx，再根据牛顿第二定律，简谐振动的加速度表达式为：

\[a = - \frac{k}{m}x\]

式中>式中k为弹簧的劲度系数，m为振子的质量，在此程序中设置为：k=2 N/m，m=2 kg。由物理知识可知，此弹簧振子的周期T=2π\(\sqrt {\frac{m}{k}} \)≈6.28 s，振幅A=\(\sqrt {\frac{m}{k}} \)v=200 m。

可以通过下面的程序验证一下：

import { Render } from "../../src/render/Render";
import { World } from "../../src/World";
import { Body } from "../../src/objects/Body";

export class test {
    world: World;
    circleBody: Body
    render: Render;

canvas: HTMLCanvasElement;
// 设置弹簧劲度系数和振子质量
k: number = 2;
m: number = 2;

    public constructor() {
        this.canvas = <HTMLCanvasElement>document.getElementById('canvas');
        this.render = new Render(this.canvas.getContext("2d"));
        // 初始化引擎
        this.world = new World();
        // 设置物体的初位置、初速度
        this.circleBody = new Body();
        this.circleBody.x = 400;
        this.circleBody.velocity = 200;
        this.world.addBody(this.circleBody);

        this.Update();
    };

    private previousTime: number;         // 上一帧的开始时刻
    private elapsedTime: number;          // 每帧流逝的时间（毫秒）

    Update() {
        requestAnimationFrame(() => this.Update());

        const time: number = performance.now();
        this.elapsedTime = this.previousTime ? (time - this.previousTime) / 1000 : 0;
        this.previousTime = time;

        if (this.elapsedTime > 0) {
            // 设置物体的加速度
            this.circleBody.acceleration = -(this.k / this.m) * (this.circleBody.x - 400);
            this.world.step(this.elapsedTime);
        };
        this.render.draw(this.world);
    };
}

window.onload = () => {
    var main: test = new test();
}

3、变加速直线运动

下面的这道题目为2011年上海高考题，原题如下：

电阻可忽略的光滑平行金属导轨长 s ＝ 1.15 m，两导轨间距 L ＝ 0.75 m，导轨倾角为 30°，导轨上端 ab 接一阻值 R ＝ 1.5 Ω 的电阻，磁感应强度 B ＝ 0.8 T 的匀强磁场垂直轨道平面向上。阻值 r ＝ 0.5 Ω，质量 m ＝ 0.2 kg 的金属棒与轨道垂直且接触良好，从轨道上端 ab 处由静止开始下滑至底端，在此过程中金属棒产生的焦耳热 Qr ＝ 0.1 J。（取 g ＝10 m/s2）求：

（3）金属棒下滑的最大速度 vm。

【讨论】这里关注的是第（3）小问，最大速度 vm的答案为 2.74 m/s。限于高中生的知识局限，只能用动能定理解决，并需要告知金属棒产生的热量。

【解】Q＝QR＋Qr＝0.4 J

\[\begin{array}{l}mg\sin 30^\circ - Q{\rm{ = }}\frac{1}{2}mv_m^2\\{v_m} = \sqrt {2g\sin 30^\circ - \frac{{2Q}}{m}} = \sqrt {2 \times 10 \times 1.15 \times 0.5 - \frac{{2 \times 0.4}}{{0.2}}} {\rm{m/s}} = 2.74{\rm{m/s}}\end{array}\]

而如果运用微积分知识是可以直接求得速度大小的。

若只需求得s与v的函数关系，解法如下：

由牛顿第二定律可知：

\[mg\sin \theta - \frac{{{B^2}{l^2}v}}{{R + r}} = ma\]

代入数据可得v和a的关系式：

\[a = 5 - 0.9v\]

对应的微分方程为：

\[\frac{{ds}}{{dv}} = \frac{v}{a} = \frac{v}{{5 - 0.9v}}\]

使用分离变量法解此方程：

\(ds = \frac{v}{{5 - 0.9v}}dv\)，初始条件为s|v=0＝0

\[s = \frac{1}{{0.81}}( - 0.9v - 5\ln ( - 0.9v + 5) + 5\ln 5)\]

将 s＝1.15 m 代入以上函数可解得：v ＝ 2.74 m/s。

若还需要求时间t，可以写出以下微分方程

\(\frac{{dv}}{{dt}} = a = 5 - 0.9v\)，v|t＝0＝0

解得

\[t = \frac{{10}}{9}[\ln 5 - \ln ( - 0.9v + 5)]\]

或

\[v = \frac{{50}}{9}(1 - {e^{ - 0.9t}})\]

将v＝2.74 m/s代入以上函数，可求得t＝0.75515 s。

进一步利用以下微分方程，还可以求出s与t的函数关系：

\(\frac{{ds}}{{dt}} = v = \frac{{50}}{9}(1 - {e^{ - 0.9t}})\)，s|t＝0＝0

解得

\[s = \frac{{450t + 500{e^{ - 0.9t}} - 500}}{{81}}\]

将s＝1.15 m代入以上函数，可求得t＝0.75484 s。

下面用物理引擎模拟这个过程并验证结果，代码如下：

import { Render } from "../../src/render/Render";
import { World } from "../../src/World";
import { Body } from "../../src/objects/Body";

export class test {
    world: World;
    circleBody: Body;

    public constructor() {
        this.world = new World();
        this.circleBody = new Body();
        this.world.addBody(this.circleBody);

        this.Update();
    };

    private previousTime: number;         // 上一帧的开始时刻
    private elapsedTime: number;          // 每帧流逝的时间（毫秒）

    Update() {
        requestAnimationFrame(() => this.Update());

        const time: number = performance.now();
        this.elapsedTime = this.previousTime ? (time - this.previousTime) / 1000 : 0;
        this.previousTime = time;

        if (this.circleBody.x >= 1.15) {
            return;
        }

        if (this.elapsedTime > 0) {
            this.circleBody.acceleration = 5 - 0.9 * this.circleBody.velocity;
            this.world.step(this.elapsedTime);
        };
    };
}

window.onload = () => {
    var main: test = new test();
}
时间：0.00s
速度：0.00m/s

模拟的结果t≈0.750 s，v≈2.70 m/s，都要比精确值来得小。

最后，以上代码都托管在：https://github.com/fjphysics/StunPhysics/。

文件下载（已下载 5 次）

发布时间：2019/8/10 下午11:55:28  阅读次数：4550

2006 - 2025，推荐分辨率 1024*768 以上，推荐浏览器 Chrome、Edge 等现代浏览器，截止 2021 年 12 月 5 日的访问次数：1872 万 9823。 站长邮箱

沪 ICP 备 18037240 号-1，

沪公网安备 31011002002865 号