伽耳顿板的模拟(动画)

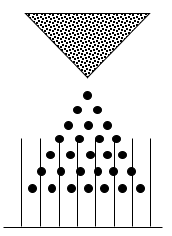
如图1所示装置，下面是等间隔的竖槽，中间是规则排列的横杆，上面容器中装有大量颗粒。将容器底部的小口打开，大量颗粒从上向下泻下来，与各级横杆碰撞后落入槽中。这种实验装置称为伽耳顿板。模拟颗粒运动的轨迹，统计落入槽中的颗粒数以及占总粒子数的比例。

解析

大量粒子从伽耳顿板下面的小口泻下来之后，在各层与横杆碰撞，最后落在各个竖槽中。实验表明：中部槽中的粒子数最多，越往两边，槽中的粒子数越少。

假设一个粒子落下来都会与每层中的一个横杆发生碰撞，碰撞后向左和向右运动的可能性(概率)相等。当粒子落下来之后，各个竖槽中的粒子数与总数的比例近似按二项式分布。

根据二项式定理可得

\[{(a + b)^n} = {a^n} + n{a^{n - 1}}b + ... + C_n^m{a^{n - m}}{b^m} + ... + na{b^{n - 1}} + {b^n}\]

其中

C\[C_n^m = \frac{{n!}}{{m!(n - m)!}}\]

令a=b=1，则得

\[1 = \frac{1}{{{2^n}}}(1 + n + \ldots + C_n^m + \ldots + n + 1)\]

取

\[P_n^m = \frac{{C_n^m}}{{{2^n}}} = \frac{{n!}}{{m!(n - m)!{2^n}}}\]

这就是2ⁿ个粒子落在第m个槽中的概率。

图示

如图2所示，对于n=8的情况，粒子落在各槽中的理论概率(%)分别为

0.391、3.13、10.9、21.9、27.3、21.9、10.9、3.13、0.391

对于2¹⁰=1024个粒子，根据各槽中的粒子数可知实际各槽中的概率(%)分别为

0.488、3.03、11.6、22.5、27.1、23.3、8.98、2.64、0.293

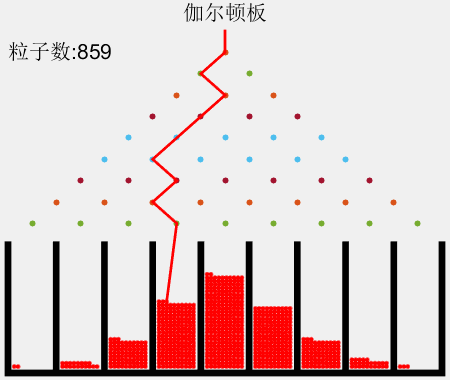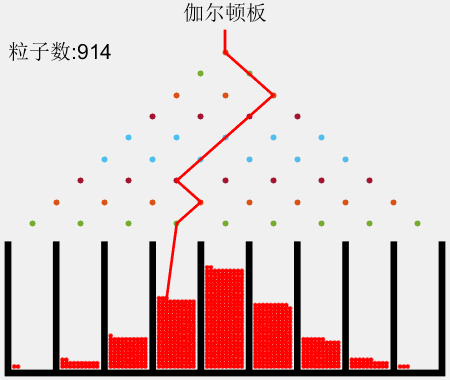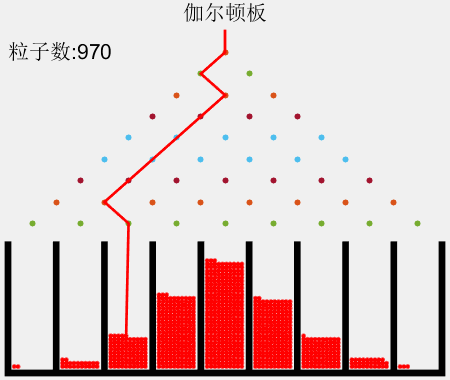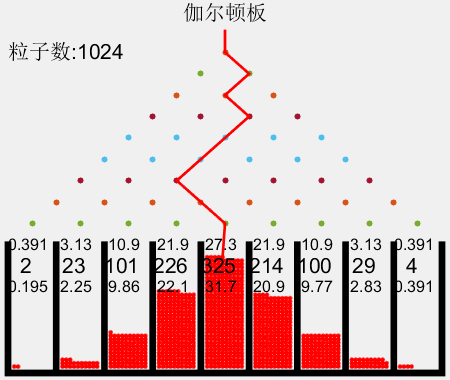
可见：粒子的分布近似于二项式分布。每次实验的结果不同（图略），但是每次实验值都在二项式分布的理论值附近波动，称为涨落。大量实验的平均值就趋于理论值。

算法

对于在0到l之间均匀分布的任意一个随机数，表示一个与横杆碰撞前的粒子。如果随机数大于0.5，表示粒子与横杆碰撞后向右偏；如果随机数小于0.5，表示粒子与横杆碰撞后向左偏。将此随机数乘以2，则整数部分为1表示粒子与横杆碰撞后向右偏；整数部分为0表示粒子与横杆碰撞后向左偏。此随机数乘以2的小数部分又当成新的随机数，同样乘以2，由其整数部分决定向哪个方向偏。整数累加的结果就是粒子落在槽的编号。对于大量的均匀分布的随机数，经过这样的方法处理后，就可统计各个槽中的粒子数。一个槽中的粒子数与总粒子数的比值就近似表示了粒子落在这个槽中的概率。

程序

%伽尔顿板的动画

%伽尔顿板的动画
clear                                  %清除变量
%rand('state',0)                        %随机状态清零(可重复相同的演示)
m=9;                                   %层数
f=zeros(1,m);                          %各层元素清零
figure                                 %创建图形窗口
hold on                                %保持图像
axis off                               %隐去坐标
mw=6;                                  %挡板高度
axis([-m,m,-m-mw,1])                   %图形范围
title('伽尔顿板','FontSize',16)        %标题
for i=1:m                              %按层循环
     for j=1:i                          %按列循环
         plot(2*j-i-1,-i+1,'.','MarkerSize',16)%画点（1）
     end                                %结束循环
    plot(2*(1:i)-i-1,ones(1,i)*(-i+1),'.','MarkerSize',16)%画点(可代替内循环)
end                                    %结束循环
x=-m:2:m;                              %隔板横坐标
w=10;                                  %一层粒子个数
s=0;                                   %粒子数清零
plot([x;x],[-m;-(m+mw)]*ones(size(x)),'k','LineWidth',5)%画隔板（2）
plot([-m,m],[-m-mw,-m-mw],'k','LineWidth',5)%画底板（2）
h=plot(0,0,'r-','LineWidth',2);        %画点取句柄
ht=text(-m,0,'粒子数:0','FontSize',16);%粒子数句柄
pause                                  %暂停
yy=1:-1:-m+1;                          %各层编号(纵坐标)
%while 1                                %无限循环
%    if get(gcf,'CurrentCharacter')==char(27) break,end%按ESC键退出
while get(gcf,'CurrentCharacter')~=char(27)%不按ESC键循环（3）
    xx=[0,0];                          %粒子初始横坐标
    x=rand;                            %取一个随机数
    s=s+1;                             %粒子数加1
    j=1;                               %第一个槽号(列标)
    for i=2:m                          %按层循环
        x=2*x;                         %随机数乘以2
        xi=floor(x);                   %取整数（4）
        j=j+xi;                        %取通道
        xx=[xx,2*j-i-1];               %连接横坐标
        x=x-xi;                        %取小数部分（5）
    end                                %结束循环
    f(j)=f(j)+1;                       %最后一层槽中粒子数加1
    t=f(j);                            %取粒子数（6）
    iy=floor((t-1)/w);                 %计算粒子叠放的层数
    ix=t-w*iy;                         %计算粒子叠放的列数
    x=2*j-m-1.9+ix*0.16;               %粒子叠放的横坐标
    y=-m-mw+iy*0.16+0.3;               %粒子叠放的纵坐标
    plot(x,y,'r.','MarkerSize',10)     %画粒子
    set(h,'XData',[xx,x],'YData',[yy,y]);%设置坐标显示轨迹（7）
    set(ht,'String',['粒子数:',num2str(s)])%显示粒子数
    drawnow                            %刷新屏幕
    pause(0.1)                         %延时
    if s==1024;break,end               %达到1024个时结束（8）
end                                    %结束循环
x=2*(1:m)-m-2;                         %数据横坐标向量
y=ones(size(x));                       %纵坐标向量
text(x,-10*y,num2str(f'),'FontSize',16)%显示粒子数
text(x,-11*y,num2str(f'/s*100,3),'FontSize',12)%显示百分比
n=1:m-1;                               %整数向量
p=[1,cumprod(fliplr(n))./cumprod(n)]/2^(m-1)*100;%二项式分布的概率（9）
%n=0:m-1;                               %整数向量
%c=factorial(m-1)./factorial(n)./factorial(m-1-n)/2^(m-1)*100;%同上
text(x,-9*y,num2str(p',3),'FontSize',12)%显示概率（10）

说明

（1）在循环中画点，表示横杆。

（2）画线表示凹槽，与横杆一起表示伽尔顿板的框架。

（3）如果要在演示过程中提示结束，就按Esc键。

（4）取随机数的整数部分，如杲为0，则槽号不变；如果为1，则槽号加1。

（5）根据槽号连接横坐标。取出小数部分当做新的随机数。

（6）累加最后一层某槽中的粒子数，由粒子数决定粒子叠放的坐标。

（7）画线显示粒子从上向下落在槽中的轨迹，从而模拟全部粒子下落的过程。

（8）演示的粒子最多达到1024个，也就是2¹⁰个，以便计算二项式的概率。

（9）用累积求积函数cumprod求二项式分布的概率。用阶乘函数factorial更简单。

n = 0:m - 1;c = factorial(m - 1)./factorial(n)./factorial(m - 1 - n)/2^(m - 1)*100;

（10）重新执行程序，表示重新做实验。每次实验的结果都不完全相同。

发布时间：2019/5/22 上午11:47:07  阅读次数：4546