第一章 四、气体

气体分子运动的特点

与固体、液体相比，气体是很容易压缩的，这说明气体分子不像固体分子或液体分子那样距离很近，气体分子之间有很大的空隙。气体能够充满整个容器，表明气体分子除了在相互碰撞的短暂时间外，相互作用力十分微弱，气体分子可以自由地运动。实际上，气体分子运动的速率很大，常温下多数气体分子的速率都达到数百米每秒——这在数量级上相当于子弹的速率。

气体的压强

我们已经知道，大气对物体的表面会产生压强。密封容器中的气体对器壁是不是也有压强？

演示

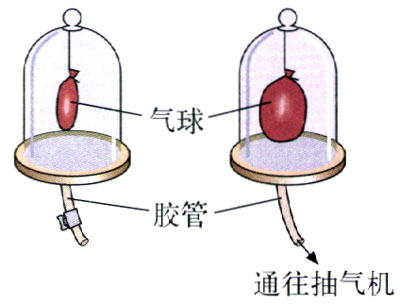
在玻璃罩内放一个充气不多的气球（图1.4-1），球皮是否受到球内气体的压强？用抽气机气机把玻璃罩内的空气抽去，抽气的过程中会看到什么现象？

抽气的过程中气球在膨胀。这说明球内的气体确实对球皮具有由内向外的压强，只是由于大气对于气球还有由外向内的压强，所以平时气球才不会胀破。

我们所说气体的压强，指的就是气体对于容器器壁的压强。

在国际单位制中，压强的单位是帕斯卡（pascal），简称帕，符号是Pa。

气体压强的微观意义

从分子动理论的观点来看，气体的压强是大量气体分子频繁地碰撞器壁而产生的。我们知道，雨滴打在雨伞上会使伞面受到冲击力，单个雨滴对伞面的作用力是微小的、短暂的，但是大量密集的雨滴接连不断地打在伞面上，就对伞面形成压力（图1.4-2）。同样，单个分子碰撞器壁的作用力是微小的、短暂的，但是大量分子频繁地碰撞器壁，就对器壁产生持续、均匀的压力。所以从分子动理论的观点来看，气体的压强就是大量气体分子作用在器壁单位面积上的平均作用力。在标准状况下，每摩尔气体的体积是22.4 L，因此1 cm³气体中大约含有2.7×10¹⁹个分子。不难想像，每秒撞击单位面积器壁的分子是极多的。大量的分子不断地撞击器壁，对器壁能产生持续的压力，就不足为奇了。

气体压强的产生可以用实验来模拟。

演示

模拟气体的压强

用小钢珠当做空气的分子。把装有钢珠的杯子拿到秤盘上方5 cm处，使1粒钢珠落在秤盘上，秤的指针会摆动一下。再在相同的高度把100粒或者更多的钢珠连续快速地倒在秤盘上（图1.4-3），秤的指针会在一个位置附近摆动。这说明大量钢珠撞击秤盘，对秤盘产生了持续的压力。在一定的时间内，碰撞的钢珠越多，对秤盘产生的压力越大。

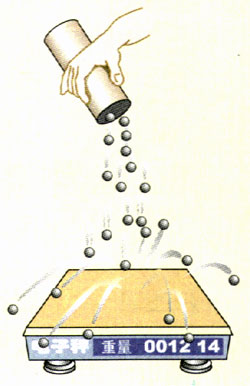
如果使这些钢珠从更高的位置落在秤盘上，可以看到秤盘所受的压力更大。这表明，钢珠的动能越大，对秤盘产生的压力越大。

可以想见，从微观角度来看，气体压强的大小与两个因素有关：一个是气体分子的平均动能，一个是分子的密集程度。

气体分子的平均动能越大，分子撞击器壁时对器壁产生的作用力越大，气体的压强就越

大；而温度是分子平均动能的标志，所以气体的压强跟温度有关。按照分子动理论，温度升高时，分子的热运动变得剧烈，分子的平均动能增大，撞击器壁时对器壁的作用力变大，所以气体的压强增大。在炎热的夏天，打足了气的自行车行驶在滚烫的路面上，有时会爆胎，这是轮胎中气体温度升高，压强增大造成的。汽车、拖拉机的内燃机，利用气体的压强与温度有关的道理，当燃油燃烧使得汽缸内气体的温度急剧升高、压强增大时，推动活塞做功。相反地，为了防止气体受热时压强加大造成安全事故，在储存压缩气体的容器上，都有明显的标示，提醒人们不要把气瓶放在高温环境中。

气体分子越密集，每秒撞击器壁单位面积的分子越多，气体的压强就越大。一定质量的气体，体积越小，分子越密集。可见，气体的压强还与体积有关。

气体分子速率的分布和统计规律

常温下，大多数气体分子运动的速率是很大的。图1.4-4给出了在0℃和100℃时具有各种速率的氧气分子所占的百分比。例如，0℃时速率在300～400 m/s之间的氧气分子占21.4%。

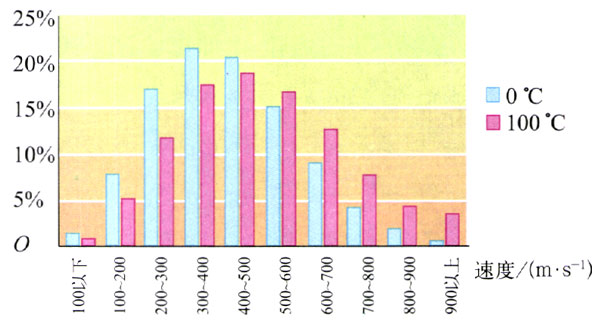
比较0℃和100℃时氧气分子的速率分布就会看到，温度较高时，速率较大的分子所占的比例大些，速率较小的分子所占的比例小些。我们说“温度越高，分子的热运动越剧烈”，就是这个意思。

我们也要看到，即使温度较高，也有少数分子的速率在100 m/s以下。至于哪个分子在什么时刻具有多大的速率，这完全是偶然的。但是，对于一定种类的大量分子来说，在一定温度时，处于一定速率范围内的分子数所占的百分比是确定的，呈现出一定的规律性，这种规律是一种统计规律（statistical law）。

演示

伽耳顿板实验

如图1.4-5所示，在一决竖直放置的木板上均匀地钉着许多铁钉，下部用隔板分割成许多等宽的竖直狭槽。这种实验装置叫做伽耳顿板。

从伽耳顿板顶部漏斗形入口投入一个小球，小球在下落时会与许多铁钉相碰，最后落入某一个狭槽内。重复几次实验，可以发现，小球每次落入的狭槽不一定相同。这表示，对单个小球的一次下落来说，落入哪个狭槽具有偶然性。

向入口投入大量小球，观察这些小球落下后在狭槽内的分布（图1.4-6）。用数量不同的小球反复做伽尔顿板实验，还可以观察到：当小球总数较少时，各次实验得到的分布情况有明显差别；当小球的总数很多时，每次得到的分布情况几乎都相同。

实验表明，虽然单个小球落入哪个狭槽具有偶然性，但大量小球在狭槽内的分布却具有一定的规律性。这就是大量偶然事件在整体上表现出来的统计规律。

在气体中，大量分子做无规则的热运动，分子以不同的速率沿着各个方向运动。分子间频繁的碰撞，使每个分子速度的大小和方向频繁地发生改变。一个分子在某一时刻的速度具有怎样的大小和方向，完全是偶然的。我们不可能跟踪每个分子的运动，也没有必要知道每个分子在某一时刻的运动状态，需要知道的是大量分子整体上所遵循的统计规律，因此，统计规律在研究热现象时具有重要的作用。

在生活中这种现象也很普遍，例如人群中各个年龄段的人数所占的百分比的分布、拥有不同数量的财产的人数在人群中所占的百分比的分布、具有某种不同健康指数的人数所占的百分比的分布，等等。这种统计规律，对医学、社会学的研究也很有意义。

大家谈

测量全班同学的身高，分别统计身高158～160 cm、161～163 cm、164～166 cm……的人数，然后以身高为横坐标、人数为纵坐标作出直方图，看看有什么规律。还可以男女生分别统计，看看身高与年龄的关系有什么性别差异。

统计规律是对大量偶然事件整体上起作用的规律，它表现了这些事物的整体特征和必然联系，在这里，个别事物的特征和偶然联系退居次要地位。在研究气体时，尽管我们认为每个粒子的运动仍然遵循力学的规律，但当体系中所包含的粒子数目极多时，就导致全新规律的出现，在这里发生了从量变到质变的飞跃。

问题和练习

1．要使汽车轮胎内空气的压强相同，冬天和夏天相比，打入胎内的空气质量相同吗？何时打入的空气质量较大？

2．用气体分子热运动的观点解释以下现象：

（1）一定质量的气体，如果保持气体的温度不变，体积越小，压强越大；

（2）一定质量的气体，如果保持气体的体积不变，温度越高，压强越大。

3．在失重的情况下气体对于器壁是否还有压强？你是根据什么道理得出结论的？有什么现象或实验可以证实你的结论？

4．用生活中的事例说明，大量出现的某类事件会表现出统计规律。

发布时间：2018/5/9 下午1:50:15  阅读次数：2150