等量电荷的电场线和等势线

等量异种电荷

解析

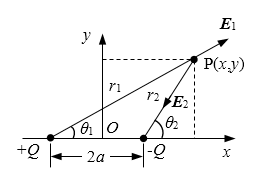如图所示，等量异号点电荷在场点P(x,y)产生的电势为

\[U = k\frac{Q}{{{r_1}}} - k\frac{Q}{{{r_2}}}\]

其中，k为静电力常量，r₁和r₂是场点P到电荷的距离

\[{r_1} = \sqrt {{{(x + a)}^2} + {y^2}} \]

\[{r_2} = \sqrt {{{(x - a)}^2} + {y^2}} \]

电场强度可根据电势梯度计算

\[E = - \nabla U\]

在直角坐标系中，劈形算符为

\[\nabla = \frac{\partial }{{\partial x}}{\bf{i}} + \frac{\partial }{{\partial y}}{\bf{j}} + \frac{\partial }{{\partial z}}{\bf{k}}\]

在Oxy平面上，场强只有两个分量

\[{E_x} = - \frac{{\partial U}}{{\partial x}},{E_y} = - \frac{{\partial U}}{{\partial y}}\]

两个点电荷在P点产生的电场强度的大小分别为

\[{E_1} = \frac{{kQ}}{{r_1^2}},{E_2} = \frac{{kQ}}{{r_2^2}}\]

场强的两个分量也能根据公式计算：

\[{E_x} = {E_1}\cos {\theta _1} - {E_2}\cos {\theta _2} = \frac{{kQ(x + a)}}{{r_1^3}} - \frac{{kQ(x - a)}}{{r_2^3}}\]

\[{E_y} = {E_1}\sin {\theta _1} - {E_2}\sin {\theta _2} = \frac{{kQy}}{{r_1^3}} - \frac{{kQy}}{{r_2^3}}\]

电场线的微分方程为

\[\frac{{dy}}{{dx}} = \frac{{{E_y}}}{{{E_x}}}\]

算法

取a为坐标单位，则电势可表示为

\[U = {U_0}(\frac{1}{{r_1^* - r_2^*}})\]

其中，U₀=kQ/a。U₀是Q在原点产生的电势，作为电势的单位。r₁*和r₂*是约化距离，分别表示为

\[r_1^* = \frac{{{r_1}}}{a} = \sqrt {{{({x^*} + 1)}^2} + {y^{*2}}} ,r_2^* = \frac{{{r_2}}}{a} = \sqrt {{{({x^*} - 1)}^2} + {y^{*2}}} \]

其中，x*=x/a，y*=y/a，x*和y*是无量纲的坐标或约化坐标。

场强的x分量用梯度可表示为

\[{E_x} = - \frac{{\partial U}}{{\partial x}} = - \frac{{{U_0}}}{a} \cdot \frac{{\partial (U/{U_0})}}{{\partial (x/a)}}\]

即

\[{E_x} = - {E_0}\frac{{\partial {U^*}}}{{\partial {x^*}}}\]

其中，E₀=U₀/a=kQ/a²，U*=U/U₀。E₀是场强的单位，U*是无量纲的电势。同理可得

\[{E_y} = - {E_0}\frac{{\partial {U^*}}}{{\partial {y^*}}}\]

两个点电荷的电场强度的两个分量用公式可表示为

\[{E_x} = {E_0}(\frac{{{x^*} + 1}}{{r_1^{*3}}} + \frac{{{x^*} - 1}}{{r_2^{*3}}}),{E_y} = {E_0}(\frac{{{y^*}}}{{r_1^{*3}}} + \frac{{{y^*}}}{{r_2^{*3}}})\]

电场线的微分方程为

\[\frac{{d{y^*}}}{{d{x^*}}} = \frac{{E_y^*}}{{E_x^*}}\]

其中E_x*=E_x/E₀，E_y*=E_y/E₀。将物理量无量纲化之后，只要做纯数值计算就行了。

MATLAB的梯度函数gradient可直接计算场强的数值分量，场强的数值解和解析解可相互比较。根据电势公式，等势线可用等值线指令contour绘制；根据电场线的微分方程，电场线可用流线指令streamline绘制。

程序

%等量异号点电荷的电场线和等势线(请在“创建图形窗口”处设置断点，以观察画图过程)
clear                                  %清除变量
xm=2.5;                                %横坐标范围
ym=2;                                  %纵坐标范围
x=linspace(-xm,xm,400);                %横坐标向量
y=linspace(-ym,ym,400);                %纵坐标向量(1)
[X,Y]=meshgrid(x,y);                   %坐标网点(矩阵)
R1=sqrt((X+1).^2+Y.^2);                %左边第一个正电荷到场点的距离
R2=sqrt((X-1).^2+Y.^2);                %右边第二个负电荷到场点的距离
U=1./R1-1./R2;                         %计算电势
u=-4:0.5:4;                            %等势线的电势向量(2)
figure                                 %创建图形窗口
C=contour(X,Y,U,u,'LineWidth',2);      %画等势线并取等势线的坐标(3)
%[C,h]=contour(X,Y,U,u);                %画等值线并取坐标矩阵和句柄(6.5版用)
%set(h,'LineWidth',2)                   %加粗曲线
clabel(C,'FontSize',16)                %标记等势线的值(4)
hold on                                %保持图像
plot([-xm;xm],[0;0],[0;0],[-ym;ym])    %画水平和竖直线
plot(-1,0,'o',1,0,'o','MarkerSize',12) %画电荷

[Ex,Ey]=gradient(-U,x(2)-x(1),y(2)-y(1));%用电势梯度求场强的两个分量(5)
%[Ex,Ey]=gradient(-U);                  %用电势梯度求场强的两个分量
axis equal tight                       %使坐标间隔相等
dth=20;                                %电场线角度间隔(6)
th=(dth:dth:360-dth)*pi/180;           %电场线的起始角度
r0=0.1;                                %电场线起点半径
x0=r0*cos(th);                         %电场线的起点横坐标
y0=r0*sin(th);                         %电场线的起点纵坐标(7)
streamline(X,Y,Ex,Ey,x0-1,y0)          %画左边电场线(中间部分达到右边)(8)
streamline(X,Y,-Ex,-Ey,x0+1,y0)        %画右边电场线(中间部分达到左边)(9)
grid on                                %加网格
title('等量异号点电荷的电场线和等势线','FontSize',20)%显示标题
xlabel('\itx/a','FontSize',16)         %显示横坐标
ylabel('\ity/a','FontSize',16)         %显示纵坐标
text(-xm,ym-0.5,'电势单位:\itkQ/a','FontSize',16)%显示电势单位
Ex=(X+1)./R1.^3-(X-1)./R2.^3;          %用公式求场强的x分量(10)
Ey=Y./R1.^3-Y./R2.^3;                  %用公式求场强的y分量
h=streamline(X,Y,Ex,Ey,x0-1,y0);       %重画左边电场线并取句柄(11)
set(h,'LineWidth',2)                   %加粗曲线
h=streamline(X,Y,-Ex,-Ey,x0+1,y0);     %重画右边电场线并取句柄
set(h,'LineWidth',2)                   %加粗曲线

说明

（1）当r/a=±1时，电场和电场强度为无穷大，这两点称为奇点。用linspacc形成对称的变量可绕过奇点。坐标间隔越小，用梯度计算场强的分量就越精确。但是，如果矩阵太大，则内存可能不够。

（2）根据公式计算无量纲的电势。等势线向量在调试程序后选取，最高电势取4U₀，最低电势取-4U₀。

（3）用contour指令画等势线的同时取出等势线的坐标。不过，6.5版不能在指令中直接使用绒宽属性，此指令可改写为两条

%[C,h]=contour(X,Y,U,u);                %画等值线并取坐标矩阵和句柄(6.5版用)
%set(h,'LineWidth',2)                   %加粗曲线

（4）等值线标签指令clabel可对等势线标记数值。

（5）梯度函数gradient根据电势求电场强度的两个分量，第一个参数要用负的电势，第二个参数表示横坐标的间隔，第三个参数表示纵坐标的间隔。如果只需要计算两个差分，后面两个参数就能省去。gradient函数还能求三维数值梯度，也能求一维数值梯度，这就是数值导数。

（6）电场线的角度间隔可自由选取，但是应该能被180整除。

（7）以电荷为中心，以r₀为半径，求电场线的相对端点坐标，由此决定左边和右边电场线的起点或终点坐标。

（8）流线指令streamline专门画流线，包括电场线，指令的第一对参数是坐标分量，第二对参数是场强分量，第三对参数是电场线的起点坐标。注意：电场线从电势高的方向指向电势低的方向，左边是正电荷，左边电场线的起点坐标是x0-1和y0，中间部分的电场线可以直接延续到负电荷。

（9）右边负电荷还要补画一些电场线。由于电场线总是从电势高的地方指向电势低的地方，所以要将电场强度的方向反向，也就是将正负电荷当相反的电荷处理。右边电场线的起点坐标是x0+1和y0。左右电荷的电场线在中间部分正好重叠。

（10）再用电场强度的公式计算分量。

（11）取句柄后可加粗电场线。用解析解画出的电场线与数值解画出的电场线基本重叠，说明用梯度函数计算偏导数是正确的。注意：如果坐标间隔取得较稀，两种方法画出的电场线就不一定重合，所以横坐标和纵坐标都取400个点。

图示

如图所示，左边表示正电荷，右边表示负电荷，等量异号点电荷的电场线和等势线关于原点是对称分布的。电场线从正电荷出发，终止于负电荷。电场线与等势线垂直，任何两条电场线都不相交。除了电势为零的直线外，等势线分别包围着各自的电荷。电场强度大的地方，电场线较密，等势线也较密。

在程序中将计算电势的公式由U=1./R1-1./R2改为U=4./R1-1./R2，即可画出非等量电荷的电场线和等势线，其中左边电荷的电量为右边的4倍。

高考点击

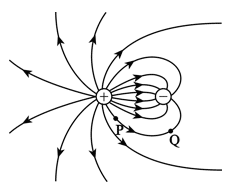【2009年北京理综13】 某静电场的电场线分布如图所示，图中P、Q两点的电场强度分别为E_P和E_Q，电势分别为U_P和U_Q。则（       A     ）

（A）E_P＞E_Q，U_P＞U_Q              （B）E_P＞E_Q，U_P＜U_Q

（C）E_P＜E_Q，U_P＞U_Q              （D）E_P＜E_Q，U_P＜U_Q

【2015年上海高考8】两个正、负点电荷周围电场线分布如图所示。P、Q为电场中两点，则（  D  ）

（A）正电荷由P静止释放能运动到Q

（B）正电荷在P的加速度小于在Q的加速度

（C）负电荷在P的电势能高于在Q的电势能

（D）负电荷从P移动到Q，其间必有一点电势能为零

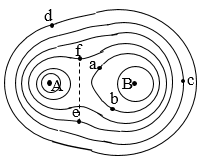
【2013年上海高考10】  两异种点电荷电场中的部分等势面如图所示，已知A点电势高于B点电势。若位于a、b处点电荷的电荷量大小分别为q_a和q_b，则（  B  ）

（A）a处为正电荷，q_a＜q_b

（B）a处为正电荷，q_a＞q_b

（C）a处为负电荷，q_a＜q_b

（D）a处为负电荷，q_a＞q_b

等量同种电荷

程序

clear %清除变量
q= 1; %电量比
xm = 2.5; %横坐标范围
ym = 2; %纵坐标范围
x= linspace(-xm,xm ); %横坐标向量
y= linspace(-ym ,ym); %纵坐标向量
[X,Y ]= meshgrid(x,y); %设置坐标网点
R1= sqrt((X + 1).^2+ Y.^2); %第一个正电荷到场点的距离
R2= sqrt((X -1).^2 + Y.^2); %第二个正电荷到场点的距离
U = 1./R1+q./R2; %计算电势
u=1:0.5:4; %等势线的电势向量
figure %创建图形窗口
contour(X,Y,U,u) %画等势线
grid on %加网格
hold on %保持图像
plot([-xm;xm],[0;0]) %画水平线
plot([0;0],[-ym;ym]) %画竖直线
plot(-1,0,'o','MarkerSize',12) %画第一个正电荷
plot(1,0,'o','MarkerSize',12) %画第二个正电荷
[Ex,Ey]= gradient(-U,x(2)-x(1),y(2)-y(1));%用电势梯度求场强的两个分量
dth1 = 20; %左边电场线角度间隔
th1= (dth1:dth1:180-dth1)*pi/180; %电场线的起始角度
x1 = 0.1 * cos(th1)-1; %电场线的起点横坐标
y1 = 0.1 * sin(th1); %电场线的起点纵坐标
streamline(X,Y,Ex,Ey,x1,y1) %画左上电场线
streamline(X,-Y,Ex,-Ey,x1,-y1) %画左下电场线
dth2= dth1/q; %右边电场线角度间隔
th2 = (180-dth2:-dth2:dth2)*pi/180;%电场线的起始角度
x2 = 0.1*cos(th2)+1; %电场线的起点横坐标
y2 = 0.1*sin(th2); %电场线的起点纵坐标
streamline(X,Y,Ex,Ey,x2,y2) %画右上电场线
streamline(X,-Y,Ex,-Ey,x2,-y2) %画右下电场线

图示

在代码中将电荷比q=1改为q=2，即可画出非等量同种电荷的电场线和等势线，如下图所示：

高考点击

【2009年上海高考7】位于A、B处的两个带有不等量负电的点电荷在平面内电势分布如图所示，图中实线表示等势线，则（  CD  ）

（A）a点和b点的电场强度相同

（B）正电荷从c点移到d点，电场力做正功

（C）负电荷从a点移到c点，电场力做正功

（D）正电荷从e点沿图中虚线移到f点，电势能先减小后增大

三个点电荷

程序

clear %清除变量
xm = 2.5; %横坐标范围
ym = 2; %纵坐标范围
x= linspace(-xm,xm ); %横坐标向量
y= linspace(-ym ,ym); %纵坐标向量
[X,Y ]= meshgrid(x,y); %设置坐标网点
R1= sqrt(X.^2 + (Y-1).^2); %上方正电荷到场点的距离
R2= sqrt((X - 1).^2+ Y.^2); %左下方负电荷到场点的距离
R3= sqrt((X + 1).^2 + Y.^2); %右下方第二个负电荷到场点的距离
U = 1./R1-1./R2-1./R3; %计算电势
u=-4:0.5:4; %等势线的电势取值，从-4至4，每隔0.5取一个值
figure %创建图形窗口
contour(X,Y,U,u) %画等势线
hold on %保持图像
plot(-1,0,'o','MarkerSize',12) %画左下方负电荷
plot(1,0,'o','MarkerSize',12) %画右下方负电荷
plot(0,1,'o','MarkerSize',12) %画上方正电荷
[Ex,Ey]= gradient(-U,x(2)-x(1),y(2)-y(1));%用电势梯度求场强的两个分量
dth = 20; %电场线角度间隔
%画正电荷出发的电场线
th1= (dth:dth:360-dth)*pi/180; %电场线的起始角度
x1 = 0.1 * cos(th1); %电场线的起点横坐标
y1 = 0.1 * sin(th1)+1; %电场线的起点纵坐标
streamline(X,Y,Ex,Ey,x1,y1) %画正电荷出发的电场线
 
%画左下方负电荷的部分电场线
th2 = (160-dth:dth:340-dth)*pi/180;%电场线的起始角度
x2 = 0.1*cos(th2)-1; %电场线的起点横坐标
y2 = 0.1*sin(th2); %电场线的起点纵坐标
streamline(X,Y,-Ex,-Ey,x2,y2) %画左下方负电荷出发的部分电场线
 
%画右下方负电荷的部分电场线
th3 = (dth+200:dth:dth+380)*pi/180;%电场线的起始角度
x3 = 0.1*cos(th3)+1; %电场线的起点横坐标
y3 = 0.1*sin(th3); %电场线的起点纵坐标
streamline(X,Y,-Ex,-Ey,x3,y3) %画右下方负电荷出发的部分电场线

图示

高考点击

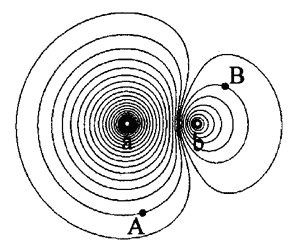
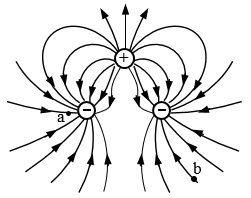【2010年上海高考9】三个点电荷电场的电场线分布如图所示，图中a、b两点处的场强大小分别为E_a、E_b，电势分别为φ_a、φ_b，则（  C  ）

（A）E_a＞E_b，φ_a＞φ_b         （B）E_a＜E_b，φ_a＜φ_b

（C）E_a＞E_b，φ_a＜φ_b         （D）E_a＜E_b，φ_a＞φ_b

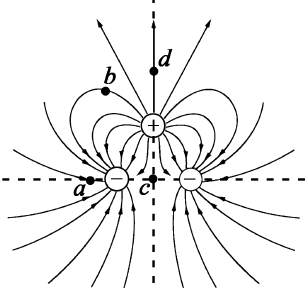【2015年江苏理综8】两个相同的负电荷和一个正电荷附近的电场线分布如图所示。c是两负电荷连线的中点，d点在正电荷的正上方，c、d到正电荷的距离相等，则（  ACD  ）

（A）a点的电场强度比b点的大

（B）a点的电势比b点的高

（C）c点的电场强度比d点的大

（D）c点的电势比d点的低

【注】此题的图中上方的左右两条电场线近似画成了直线，好像有点不对。

发布时间：2017/12/11 上午11:40:52  阅读次数：8112