第三章 二、法拉第电磁感应定律
电气化需要强大的电力。要利用电磁感应现象来获得大规模使用的电,还有许多规律要探索。例如,怎样使电磁感应获得的电压高一些,就是一个必须解决的问题。法拉第电磁感应定律的建立,为解决实际问题指明了方向,叩开了电气化的大门。
感应电动势
在电磁感应现象中,既然在闭合电路中产生了感应电流,这个电路中就一定有电动势。我们把电磁感应现象中产生的电动势叫做感应电动势(induction electromotive force)。在闭合电路里,产生感应电动势的那部分导体相当于电源。
我们知道,在一个简单电路中,两节干电池串联起来产生的电流大于一节干电池产生的电流。这说明,电源的电动势高,电路中流过的电流就大。因此在电路组成不变的情况下,根据感应电流的大小,可以判断感应电动势的大小。
在电磁感应现象中,感应电动势的大小跟什么因素有关呢?
演示
怎样使感应电动势大一些
1.我们仍然用图3.1-2和图3.1-3的装置做实验,研究影响感应电动势大小的因素。
在图3.1-2中,使导体棒以不同的速度切割磁感线,观察电流表指针偏转的幅度。我们发现:为了使感应电动势大一些,可以_______________________。
2.在图3.1-3中,使磁铁以不同的速度插入线圈和从线圈中抽出,观察电流表指针偏转的幅度。我们又发现:为了使感应电动势大一些,可以_________________________。
思考与讨论
通过前面的实验,我们知道了在不同情况下获得较大的感应电动势的方法。在这两种情况下,感应电动势的大小都与磁通量的变化有关。能不能利用磁通量的概念,把两种情况概括起来,用一句话说明什么条件下可以获得较大的感应电动势?
许多实验都表明,感应电动势的大小跟磁通量变化的快慢有关。我们用磁通量的变化率来描述磁通量变化的快慢,它是磁通量的变化量跟产生这个变化所用时间的比值。
请复习必修物理课中学习速度、加速度时关于变化率的说明。
如果时刻t1穿过闭合电路的磁通量为Φ1,时刻t2穿过闭合电路的磁通量为Φ2,在t1到t2这段时间里磁通量的变化量就是Φ2-Φ1,记为ΔΦ=Φ2-Φ1。这个变化是在Δt=t2-t1这段时间内发生的,磁通量的变化率应该表示为\(\frac{{\Delta \Phi }}{{\Delta t}}\)。
看来,磁铁与导体的相对运动速度越大,产生磁通量变化ΔΦ所用时间Δt就越小,所以\(\frac{{\Delta \Phi }}{{\Delta t}}\)就越大,产生的感应电动势也越大。
法拉第电磁感应定律
大量实验表明:电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。这就是法拉第电磁感应定律(Faraday law of electromagnetic induction)。
如果用E表示感应电动势,它的单位是伏特(V),磁通量和时间的单位分别用韦伯(Wb)和秒(s),法拉第电磁感应定律可以用公式表示为
E=\(\frac{{\Delta \Phi }}{{\Delta t}}\)
实验
多匝线圈的感应电动势
我们探究线圈的匝数与感应电动势的关系。
首先想一想,线圈的匝数与感应电动势可能有什么关系?
一个闭合电路可以看做由1匝线圈组成。如果线圈是多匝的,由于每一匝线圈中都会产生感应电动势,在多匝线圈上产生的感应电动势大概要比1匝线圈产生的感应电动势大!
我们仍然用前面的实验装置来研究,但这次选用匝数不同的两个线圈。
实验时把条形磁铁插入一个线圈和从这个线圈中抽出,然后以相同的速度插入另一个匝数不同的线圈和从这个线圈抽出。
将观察到的现象,记录在下面的表格中。
|
指针摇动的幅度 |
||
|
线圈匝数 |
磁体N极插入 |
磁体N极抽出 |
|
10匝 |
|
|
|
100匝 |
|
|
从上面的记录看,你认为感应电动势的大小跟线圈匝数的多少有什么关系?
精确的实验告诉我们,在n匝线圈组成的电路上,产生的感应电动势是
E=n\(\frac{{\Delta \Phi }}{{\Delta t}}\)
在实际工作中,为了获得较大的感应电动势,常常采用几百匝甚至几千匝的线圈。
法拉第电磁感应定律进一步揭示了电与磁的相互联系,同时也告诉我们:电能的产生一定是以消耗其他形式的能量为代价的。在前面的实验中,无论导体切割磁感线,还是把磁铁插入线圈或从线圈中抽出,都是消耗了机械能才获得了电能。而在电池中,是将化学能转变成了电能。
今天,我们使用的电能从各种形式的能转化而来:风力发电,是把空气流动的动能转化为电能;水力发电,是利用水的机械能带动发电机来发电;火力发电,是利用石油、天然气或煤燃烧时的内能,推动蒸汽轮机再带动发电机来发电……随着社会对电力需求的不断增大,人们一直在探索获取电能的更好方法。但是到目前为止,各种获得大规模电能的实用方案,都是以法拉第电磁感应定律为理论基础的,不同的只是如何来推动发电机而已。
探索者
开门时线圈中会有电流吗?
分别给门的四角钉上大钉子,用电线沿着4个钉子绕制一个几十匝的大线圈,如图3.2-1所示。线圈的两端连在一个电流表上。开门、关门时能不能发出电来?试试看!

如果发电效果不明显,想一想,应该怎样改进?
问题和练习
1.电路中感应电动势的大小,是由穿过这一电路的______所决定的。
a.磁通量
b.磁通量的变化量
c.磁通量的变化率
以上填空的三个选项,正确的显然是c,但你能说明选项a和选项b的含义吗?你认为当年安培实验时最初的猜想是哪个选项?
2.在图3.2-2中,闭合矩形线圈不动,磁体在线圈中转动,如果磁体转动的速度不同,线圈中产生的感应电动势相同吗?

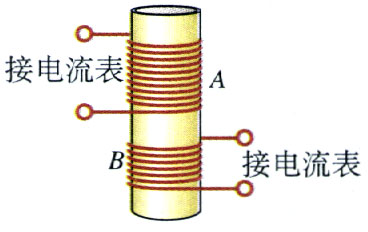
3.两个匝数不同的线圈绕在同一个圆筒上,如图3.2-3所示,它们的匝数nA>nB。当一个条形磁体穿过圆筒时,哪个线圈产生的感应电动势大些?
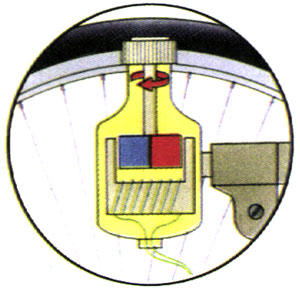
4.某自行车上有一个如图3.2-4所示的装置,滚轮靠在自行车轮胎的边缘上。自行车行驶时,滚轮带着其中的磁体转动。这个装置有什么用途?
5.桌面上放着一个单匝矩形线圈,线圈中心上方一定高度上有一竖立的条形磁体(图3.2-5),此时线圈内的磁通量为0.04 Wb。把条形磁体竖放在线圈内的桌面上时,线圈内磁通量为0.12 Wb。分别计算以下两个过程中线圈中的感应电动势。
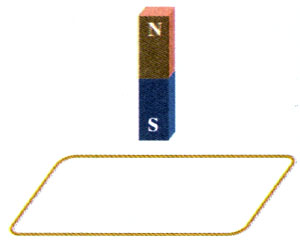
(1)把条形磁体从图中位置在0.5 s内放到线圈内的桌面上;
(2)换用10匝的矩形线圈,线圈面积和原单匝线圈相同,把条形磁体从图中位置在0.1 s内放到线圈内的桌面上。
文件下载(已下载 217 次)发布时间:2017/10/13 上午10:54:20 阅读次数:2422
