第十八章 4 玻尔的原子模型

玻尔原子理论的基本假设

丹麦物理学家N．玻尔（N．Bohr，1885-1962）意识到了经典理论在解释原子结构方面的困难。在普朗克关于黑体辐射的量子论和爱因斯坦关于光子的概念的启发下，他在1913年把微观世界中物理量取分立值的观念应用到原子系统，提出了自己的原子结构假说。

玻尔的原子结构假说包括以下两方面的内容。

轨道量子化与定态

玻尔认为，原子中的电子在库仑引力的作用下，绕原子核做圆周运动，服从经典力学的规律。但不同的是，电子运行轨道的半径不是任意的，只有当半径的大小符合一定条件时，这样的轨道才是可能的。也就是说，电子的轨道是量子化的。电子在这些轨道上绕核的转动是稳定的，不产生电磁辐射。

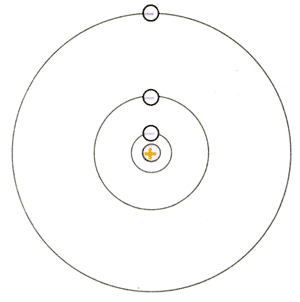
玻尔的理论与我们的日常观念有很大的不同。

人们常把原子核和它周围的电子比做太阳系或者地球和人造卫星。以地球和人造卫星为例，假如我们发射了一颗卫星，使它在一定的圆轨道上运行。如果需要，可以使这颗卫星的能量稍大一些，在更大一些的轨道上运行。只要技术条件能够达到，轨道半径可以按照需要任意取值。这种情况下，我们说，轨道半径是连续的。

但是，并非把这个图景缩小就可以看做原子核和它周围电子的运动。在玻尔的理论中，电于的轨道半径只可能是某些分立的数值。例如，氢原子中电子轨道的最小半径是0.053 nm，不可能再小了；电子还可能在半径是0.212 nm、0.477 nm……的轨道上运行，但是轨道半径不可能是介于这些数值中间的某个值！

当电子在不同的轨道上运动时，原子处于不同的状态。玻尔指出，原子在不同的状态中具有不同的能量，因此，原子的能量是量子化的。这些量子化的能量值叫做能级（energy level）。原子中这些具有确定能量的稳定状态，称为定态（stable state）。能量最低的状态叫做基态（ground state），其他的状态叫做激发态（excited state）。通常用一个或几个量子数来标志各个不同的状态，例如可以用

n＝1，2，3，…

来标志能量分别为

E₁，E₂，E₃，…

氢原子基态（n＝1）和激发态（n＝2，3，4，…）。

频率条件

按照玻尔的观点，电子在一系列定态轨道上运动，不会发生电磁辐射。那么，如何解释观察到的原子光谱呢？对此，玻尔假定：当电子从能量较高的定态轨道（其能量记为E_m）跃迁到能量较低的定态轨道（能量记为E_n，m>n）时，会放出能量为hν的光子（h是普朗克常量），这个光子的能量由前后两个能级的能量差决定，即

hν＝E_m－E_n

这个式子称为频率条件，又称辐射条件。反之，当电子吸收光子时会从较低的能量态跃迁到较高的能量态，吸收的光子的能量同样由频率条件决定。

玻尔理论对氢光谱的解释

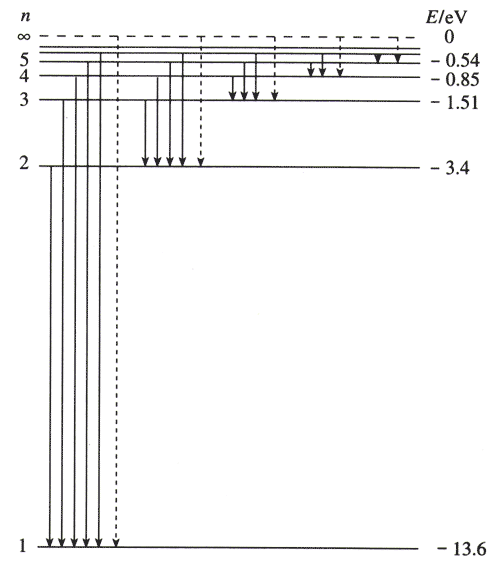
从玻尔的基本假设出发，运用经典电磁学和经典力学的理论，可以计算氢原子中电子的可能轨道半径及相应的能量。图18.4-2是氢原子的能级图。

思考与讨论

巴耳末公式中有正整数n出现，这里我们也用正整数n来标志氢原子的能级，它们之间是否有某种联系？

玻尔的频率条件告诉我们，原子从较高的能级跃迁到较低的能级时，例如从E₃跃迁到E₂时，辐射的光子的能量为hν＝E₃－E₂。按照玻尔理论，巴耳末公式中的正整数n和2，正好代表电子跃迁之前和跃迁之后所处的定态轨道的量子数n和2。因此，巴耳末公式代表的应该是电子从量子数分别为n＝3，4，5，…的能级向量子数为2的能级跃迁时发出的光谱线。按照这个思路可以根据玻尔理论推导出巴耳末公式，并从理论上算出里德伯常量R的值。这样得到的结果与实验值符合得很好。同样，玻尔理论也能很好地解释甚至预言氢原子的其他谱线系。

通常情况下，原子处于基态，基态是最稳定的。气体放电管中的原子受到高速运动的电子的撞击，有可能向上跃迁到激发态。处于激发态的原子是不稳定的，会自发地向能量较低的能级跃迁，放出光子，最终回到基态。这就是气体导电时发光的机理。

原子从高能态向低能态跃迁时放出的光子的能量等于前后两个能级之差。由于原子的能级是分立的，所以放出的光子的能量也是分立的。因此原子的发射光谱只有一些分立的亮线。

由于不同的原子具有不同的结构，能级各不相同，因此辐射（或吸收）的光子频率也不相同。这就是不同元素的原子具有不同的特征谱线的原因。

玻尔模型的局限性

玻尔的原子理论第一次将量子观念引入原子领域，提出了定态和跃迁的概念，成功地解释了氢原子光谱的实验规律。但对于稍微复杂一点的原子如氦原子，玻尔理论就无法解释它的光谱现象。这说明玻尔理论还没有完全揭示微观粒子运动的规律。它的不足之处在于保留了经典粒子的观念，把电子的运动仍然看做经典力学描述下的轨道运动。

实际上，原子中电子的坐标没有确定的值。因此，我们只能说某时刻电子在某点附近单位体积内出现的概率是多少，而不能把电子的运动看做一个具有确定坐标的质点的轨道运动。

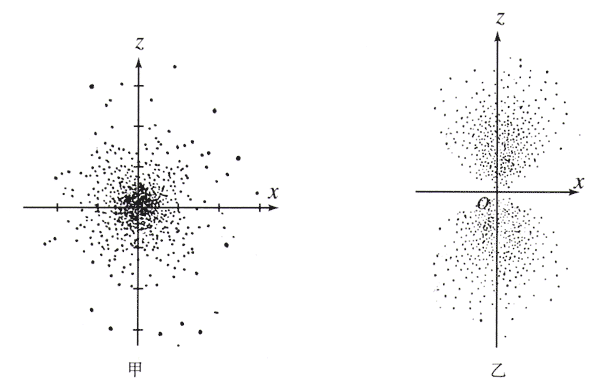
当原子处于不间的状态时，电子在各处出现的概率是不一样的。如果用疏密不同的点子表示电子在各个位置出现的概率，画出图来，就像云雾一样，可以形象地称做电子云（electron cloud）。

图18.4-4甲是氢原子处于n＝1的状态时的电子云；当n＝2时有几个可能的状态，图乙画的是其中一个状态的电子云。

科学足迹

弗兰克-赫兹实验

玻尔理论的一个重要假设是原子能量的量子化。光谱测量发现了电磁波发射或吸收的分立特征，从而证实了原子中分立的能级的存在。

然而，激发原子的手段不只是让它吸收电磁辐射，还有加热或使粒子碰撞等方式。因此，除了光谱测量外，用其他方法也应该能够证明原子能量的量子化现象，弗兰克-赫兹实验就是其中之一。

如果原子的能级是分立的，那么用碰撞的方式使原子吸收的能量，即其他粒子转移给原子的能量，也应该是量子化的。1914年，弗兰克（J．Franck）和赫兹（G．Hertz）利用电子轰击汞原子，发现电子损失的能量，也就是汞原子吸收的能量，是分立的，从而证明汞原子的能量确实是量子化的。

弗兰克-赫兹实验原理如图18.4-5所示。把汞放入抽成真空的玻璃容器，容器中就充满了汞蒸汽。容器内还密封着阴极K、金属网制成的栅极G及接收极A。阴极灯丝K通电加热后发射电子。在K与栅极G之间加电场使电子加速。在G与接收极A之间加0.5 V的反电压。当电子通过K-G空间加速后进入G-A空间时，如果能量较大，就可以克服G-A间的反向电场到达接收极A，形成电流通过电流表。

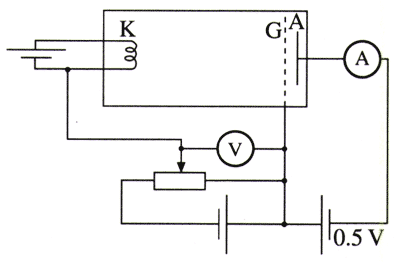
电子在K-G区域虽然由于电场加速而获得能量，但因为与汞原子碰撞，电子把自己的一部分能量交给了汞原子，剩下的能量可能很小，以致通过栅极G后无法克服G-A间的反向电压到达接收极A。如果大部分电子都是如此，那么到达接收极A的电子就很少，通过电流表的电流也很小。

实验过程中，逐渐增加K-G间的电压，记录通过电流表的电流，得到电流随K-G间电压变化的曲线，如图18.4-6所示。从图中看出，每当K-G间的电压增加4.9 V时，电流就会大幅下降。

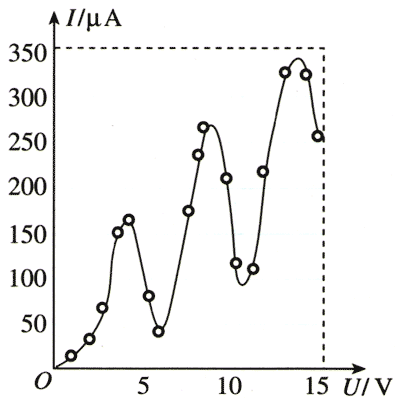
如果汞原子的能量是量子化的，而且它的基态与第一个激发态之间的能量差是4.9 eV，那就很容易解释观测到的现象。

当K-G间的电压低于4.9 V时，电子在K-G间被加速而获得的能量低于4.9 eV。此时如果电子与汞原子碰撞，由于汞原子的能量不能连续变化，所以碰撞不会使汞原子跃迁到激发态。也就是说，电子不会因碰撞损失能量，因而有足够的能量克服反向电压到达A极，形成电流。在电子能量低于4.9 eV的情况下，电子能量越高越容易克服G-A间的反向电压抵达A极，因此电流随着K-G间电压的升高也越来越大。

当K-G间电压达到4.9 V时，电子在到达G极附近时获得的能量正好是4.9 eV，与汞原子相碰时，就有很大的可能把全部能量传递给汞原子，使汞原子从基态跃迁到最近的一个能量较高（4.9 eV）的激发态。这样，电子就无法克服G-A间的反向电压到达A极，因此A极电流大幅度下降。

等到K-G间的电压超过4.9 V较多时，电子在K-G空间与汞原子碰撞而转移掉4.9 eV的能量后，还留有足够的能量，又能克服反向电压从G极到达A极，电流又上升了。

当K-G间的电压是4.9 V的2倍或3倍时，电子在K-G空间有可能经过两次或三次碰撞而耗尽能量，从而使电流再次下降。

这样我们就根据汞原子能量量子化的假设解释了图18.4-6的实验结果。

STS

从量子力学的诞生看科学技术与社会

20世纪初是群英辈出的时代。从量子化的概念首次提出到描述微观粒子运动的量子力学的诞生，历经了大约四分之一个世纪。在通往量子论的道路上，闪耀着普朗克、爱因斯坦、玻尔、海森伯、德布罗意、薛定谔、玻恩和狄拉克等一大批杰出的物理学家的光辉的名字。

现代物理学的另一支柱是相对论。与相对论的建立不同，量子理论并非主要由一个物理学家创立，它是许多物理学家共同努力的结晶。正如彼得·罗伯森在《玻尔研究所的早年岁月》一书中所说的那样，“量子物理学的建立可以认为是物理学研究工作方式上的转折点”。这种科学研究的群体性特点在20世纪后来的科学和技术研究中，例如核能的开发和利用、原子弹的研制中，都表现得十分突出。

量子力学的诞生也是与当时的社会环境分不开的。到20世纪初，英、法、德、美等国家相继完成了第二次工业革命，成为工业化的国家。电的应用使人类获得极其便利的动力的同时，也为物理学的发展奠定了技术基础。真空技术的提高使汤姆孙能够利用高真空的放电管观察阴极射线在电、磁场中的偏转，从而导致了电子的发现。这一发现动摇了原子不可分的传统观念，拉开了人类探索原子结构的序幕，进而改变了人们的生活，改变了人们的思维。

然而，前期量子理论的出现不仅源于对原子结构的探索，而且源于对黑体辐射和光电效应等问题的研究。第二次工业革命极大地推动了冶金工业的发展，而冶金对高温测量技术的需求及天文学等方面的需要则推动了对热辐射的研究。普朗克建立了与实验符合得很好的黑体辐射公式，为此他于1900年12月提出了能量量子化的概念。五年之后，爱因斯坦在此基础上进一步提出了光量子的概念，对光电效应做出了满意的理论解释。普朗克和爱因斯坦的工作使人们认识到光的波粒二象性，为量子力学的发展奠定了坚实的基础。

在原子结构方面，人们提出了各种模型和设想，如1898年汤姆孙的“枣糕模型”，1911年卢瑟福的核式结构模型等。1913年，玻尔在卢瑟福模型的基础上，结合普朗克的量子概念，提出了自己的原子结构理论。玻尔的原子理论成功地解决了卢瑟福模型的困难。然而，由于它是建立在经典理论基础上的模型，仍然有许多无法解决的难题。

1923年后，前期量子理论的困难才有了突破性进展。首先是德布罗意，他在爱因斯坦的光量子理论的启发下，提出了实物粒子的波粒二象性，使量子理论由前期阶段转入新的量子理论——量子力学的形成阶段。

量子力学是反映微观世界运动规律的正确理论，它是沿着两条不同道路发展的。一条道路源于德布罗意的物质波，并由薛定谔的波动力学最后完成；另一条道路是海森伯等通过对玻尔的对应原理等理论的深入的、批判性的研究而形成的矩阵力学。后来证明，这两种描述微观世界的理论是等价的，只是形式不同而已。至此，现代量子理论已经基本建立起来，并在以后的几十年中得以迅速完善和发展。

量子力学的建立使人类对自然界的认识由宏观世界进入到微观世界。它的诞生带来了物理学及其他科学领域的革命性变化，导致一系列新学科和边缘学科的出现，如核物理学、固体物理学、基本粒子物理学、量子化学、量子生物学等。

对量子力学、狭义相对论和原子核物理的深入研究，为人类找到了一种实际上“取之不尽，用之不竭”的新能源——核能。当量子力学被应用到固体等复杂体系时，它解释了材料为何有导体、绝缘体和半导体之分，并提出了半导体二极管、三极管等观念，后来发展为集成电路，成为现代电子计算机的技术基础。可以说，没有量子力学就没有以电子计算机控制为主导的现代化工业，就没有我们今天的信息时代。

问题与练习

1．参考图18.4-2，用玻尔理论解释，当巴耳末公式n＝5时计算出的氢原子光谱的谱线，是哪两个能级之间的跃迁造成的？

2．请用玻尔理论解释：为什么原子的发射光谱都是一些分立的亮线？

3．如果大量氢原子处在n＝3的能级，会辐射出几种频率的光？其中波长最短的光是在哪两个能级之间跃迁时发出的？

4．包含各种波长的复合光，被原子吸收了某些波长的光子后，连续光谱中这些波长的位置上便出现了暗线，这样的光谱叫做吸收光谱。请用玻尔理论解释：为什么各种原子吸收光谱中的每一条暗线都跟该种原子的发射光谱中的一条亮线相对应？

发布时间：2017/7/8 下午9:07:32  阅读次数：4710