第十六章 6 用动量概念表示牛顿第二定律

用动量概念表示牛顿第二定律

现在大家已经十分熟悉牛顿第二定律的数学表达式F=ma，但当初牛顿是通过动量表达力与运动的关系的。下面我们尝试由F＝ma出发得出力与动量变化的关系。

先假定物体受到恒力的作用，做匀变速直线运动。在时刻t物体的初速度为v，在时刻t′的末速度为v′，那么它在这个过程中的加速度就是

a=\(\frac{{v' - v}}{{t' - t}}\)

因此

F＝m\(\frac{{v' - v}}{{t' - t}}\)＝\(\frac{{mv' - mv}}{{t' - t}}\)＝\(\frac{{p' - p}}{{t' - t}}\)

由于Δp＝p′－p，Δt＝t′－t，所以

F＝\(\frac{{\Delta p}}{{\Delta t}}\)                        （1）

（1）式表示：物体动量的变化率等于它所受的力。这是牛顿第二定律的另一种表达形式。

动量定理

（1）式也可以写成

mv′－mv＝F（t′－t）                         （2）

这个式子的左边是物体在t到t′这段时间间隔中动量的增加量，右边既与力的大小、方向有关，又与力的作用时间有关。（2）式告诉我们：力越大、作用时间越长，物体的动量增加得越多。看来，F（t′－t）这个量反映了力的作用对时间的积累效应。物理学中把力与力的作用时间的乘积叫做力的冲量（impulse）。

如果用I代表一个过程中物体所受的力的冲量，用p和p′分别代表物体在过程始末的动量，那么（2）式可以写为

p′－p=I                        （3）

（3）式或（2）式表明：物体在一个过程始末的动量变化量等于它在这个过程中所受力的冲量。这个关系叫做动量定理（theorem of momentum）。

如果物体所受的力不是恒力，物体不做匀变速运动，那么可以依必修物理课中常用的方法，把过程细分为很多短暂的过程，每个过程中物体所受的力没有很大的变化，可以近似看做匀变速运动，可以应用（2）式或（3）式。把应用于每个短暂过程的关系式相加，就得到了应用于整个过程的动量定理，形式上与（2）式或（3）式完全一样。这时（1）、（2）两式中的F应该理解为力的平均值。

动量定理的物理实质与牛顿第二定律是相同的，但有时应用起来更方便，

【例题】

一个质量为0.18 kg的垒球，以25 m/s的水平速度飞向球棒，被球棒打击后，反向水平飞回，速度的大小为45 m/s。若球棒与垒球的作用时间为0.01 s，球棒对垒球的平均作用力有多大？

【分析】球棒对垒球的作用力是变力，力的作用时间很短。在这个短时间内，力先是急剧地增大，然后又急剧地减小为零。在冲击、碰撞一类问题中，相互作用的时间很短，力的变化都具有这个特点。动量定理适用于变力，因此，可以用动量定理计算球棒对垒球的平均作用力。

由题中所给的量可以算出垒球的初动量和末动量，由动量定理即可求出垒球所受的平均作用力。

【解】沿垒球飞向球棒时的方向建立坐标轴，垒球的初动量为

p＝mv＝0.18×25 kg·m/s＝4.5 kg·m/s

垒球的末动量为

p＝mv′＝0.18×45 kg·m/s=－8.1 kg·m/s

由动量定理知垒球所受的平均作用力为

F＝\(\frac{{p' - p}}{{t' - t}}\)＝\(\frac{{ - 8.1 - 4.5}}{{0.01}}\)N＝－1260 N

垒球所受的平均力的大小为1260 N，负号表示力的方向与坐标轴的方向相反，即力的方向与垒球飞来的方向相反。

从（1）、（2）两式和上面的例子我们得到这样的启示：要使物体的动量发生一定的变化，可以用较大的力作用较短的时间，也可以用较小的力作用较长的时间。

玻璃杯从一定的高度下落，落在水泥地面会破碎，落在地毯上不会破碎，怎样解释这个现象？从同样的高度落到地面，两种情况下动量的变化量是一样的，地面对杯子的力的冲量也应该一样。但是柔软的地毯对杯子的作用时间较长，因此作用力会小些，玻璃杯不易破碎。易碎物品运输时要用柔软材料包装，船舷和码头常常悬挂旧轮胎，都是为了延长作用时间以减小作用力。

科学漫步

汽车碰撞试验

汽车安全性能是当今衡量汽车品质的重要指标，也是未来汽车发展的三大主题（安全、节能、环保）之一。实车碰撞试验是综合评价汽车安全性能最有效的方法，也是各国政府检验汽车安全性能的强制手段之一。

1998年6月18日，国产轿车在清华大学汽车工程研究所进行的整车安全性碰撞试验取得成功，被誉为“中国轿车第一撞”。从此，我国汽车的整车安全性碰撞试验开始与国际接轨。

碰撞试验是让汽车以48.3 km/h的国际标准碰撞速度驶向质量为80 t的国际标准碰撞试验台。由于障碍物是固定的，所以撞击使汽车的动量一下子变到零，其冲击力相当于以100 km/h左右的速度撞向非固定物体。“轰”的一声巨响之后，试验车撞在试验台上，载着模拟乘员的崭新轿车眨眼间被撞得短了一大截。技术人员马上查看车辆受损情况：两侧安全气囊是否爆开？安全带是否发挥有效作用？前挡风玻璃是否破碎？“乘员”是否完好无损？四个车门是否能正常开启？……还要取出各种传感器，做进一步处理，通过计算机得到碰撞试验的各项数据。

在汽车碰撞试验中，“乘员”身上安装着传感器。汽车碰撞时产生的冲击力不仅很大，而且很复杂。在碰撞瞬间冲击力的波形与碰撞的速度、相撞双方的质量分布、接触处的形状、材料、变形等因素相关。人体能够承受的冲击力有多大？这与许多因素有关，其中最重要的就是力的方向，撞车时是否受伤在很大程度上要看人体受到冲击的位置。相同质量、相同车型、相同的相对速度下进行的多次碰撞，对乘员的伤害程度可能有很大的差别。

问题：轿车前面的发动机舱是不是越坚固越好？

科学足迹

历史上关于运动量度的争论

历史上，一种观点认为应该用物理量mv来量度运动的“强弱”；另一种观点认为应该用物理量mv²来量度运动的“强弱”。

主张以mv量度运动的代表人物是笛卡儿。他认为：“在物质中存在一定量的运动，它的总和在世界上永远不会增加也不会消失。”这实际上是后来所说的动量守恒定律的雏形。

主张以mv²量度运动的代表人物是莱布尼兹。他认为守恒的应该是∑mv²而不是Σmv。

经过半个多世纪的争论，法国科学家达兰贝尔（d'Alembert，1717—1788）用他的研究指出，双方实际是从不同的角度描述了运动的守恒性。

用现在的科学术语说，就是：“力”既可以通过动量来表示

F＝\(\frac{{\Delta (mv)}}{{\Delta t}}\)

又可以通过动能来表示

F＝\(\frac{{\Delta (\frac{1}{2}m{v^2})}}{{\Delta x}}\)

因此，动能\(\frac{1}{2}\)mv²决定了物体在力F的阻碍下能够运动多远；而动量mv则决定了物体在力F的阻碍下能够运动多长时间。也就是说，动量定理反映了力对时间的累积效应；动能定理反映了力对空间的累积效应。

这场争论一方面促进了机械能概念及整个能量概念的形成，并使人们对多种运动形式及其相互转变的认识更加深入，另一方面，动量与动量守恒定律也在争论中显示出它的重要性。

做一做

动量与能量之间具有密切的关系，这种关系在粒子的研究中更显得重要。

某实物粒子在速度不太大时的动能可以用它的速度v表示：E＝\(\frac{1}{2}\)mv²，请你导出用动量p表示动能的公式。同样，请你导出用动能E表示动量的公式。

问题与练习

1．在光滑水平面上，原来静止的物体在水平力F的作用下，经过时间t、通过位移l后，动量变为p、动能变为E_k。以下说法正确的是

A．在F作用下，这个物体经过位移2l，其动量将等于2p；

B．在F作用下，这个物体经过时间2t，其动量将等于2p；

C．在F作用下，这个物体经过时间2t，其动能将等于2E_k；

D．在F作用下，这个物体经过位移2l，其动能将等于2E_k。

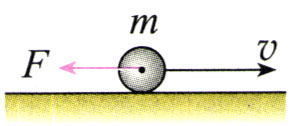
2．一个质量m＝10 kg的物体，以v＝10 m/s的速度做直线运动，受到一个反方向的作用力F（图16.6-3），经过4s，速度变为反向2 m/s。这个力是多大？

3．质量是40 kg的铁锤从5 m高处落下，打在水泥桩上，跟水泥桩撞击的时间是0.05 s。撞击时，铁锤对桩的平均冲击力有多大？

4．体操运动员在着地时总要屈腿（图16.6-4），这是为什么？

发布时间：2017/7/3 下午9:02:32  阅读次数：3030