第十六章 4 碰撞

碰撞是十分普遍的现象，特别是在有关微观粒子的探讨中，碰撞的研究起着重要的作用。

弹性碰撞和非弹性碰撞

从前两节的分析可以看到，碰撞过程遵从动量守恒定律。那么，碰撞过程也一定遵从能量守恒定律吗？例如，两个物体相碰，碰撞之前它们的动能之和与碰撞之后的动能之和相等吗？

思考与讨论

在本章第1节开始的演示中，一个钢球与另一个静止的钢球相碰，如果两个钢球的质量相等，第一个钢球停止运动，第二个钢球能摆到同样的高度．说明这个碰撞过程中没有能量损失，碰撞过程能量守恒。

碰撞过程中能量总是守恒的吗？我们分析一个例子。

如图16.4-1，两个物体的质量都是m，碰撞以前一个物体静止，另一个以速度v向它撞去。碰撞以后两个物体粘在一起，成为一个质量为2m的物体，以速度vʹ继续前进。

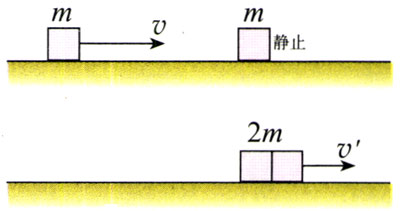
这个碰撞过程中能量（总动能）守恒吗？

可以先根据动量守恒定律求出碰撞后的共同速度vʹ，也就是用v表示vʹ，然后分别计算碰撞前后的总动能。

如果碰撞过程中机械能守恒，这样的碰撞叫做弹性碰撞（elastic collision）；如果碰撞过程中机械能不守恒，这样的碰撞叫做非弹性碰撞（inelastic collision）。

近代物理学中，经常遇到的是微观粒子间的碰撞。微观粒子碰撞时没有能量损失，所以我们重点研究弹性碰撞。

思考与讨论

我们考虑一维弹性碰撞。在本章第1节开始时的演示中，我们已经观察了两个质量相等物体的碰撞、两个质量相差悬殊的物体的碰撞，了解了它们碰撞前后速度变化的特点。现在把它们的碰撞看做弹性碰撞，从理论上分析不同情况下碰撞前后速度的变化情况。

假设物体m₁以速度v₁与原来静止的物体m₂碰撞，碰撞后它们的速度分别为v₁ʹ和v₂ʹ。我们的任务是得出用m₁、m₂、v₁表达v₁ʹ和v₂ʹ的公式。

碰撞过程遵从动量守恒定律，据此可以列出包含上述各已知量和未知量的方程。弹性碰撞中没有机械能损失，于是可以列出另一个方程。两个方程联立，把v₁ʹ和v₂ʹ作为未知量解出来就可以了。

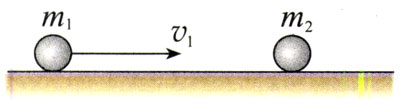
图16.4-2所示的碰撞发生后，两个物体的速度分别为

v₁ʹ＝\(\frac{{{m_1} - {m_2}}}{{{m_1} + {m_2}}}\)v₁                    （1）

v₂ʹ＝\(\frac{{2{m_1}}}{{{m_1} + {m_2}}}\)v₁                    （1）

我们对几种情况下这两个式子的结果做些分析。

• m₁＝m₂，即两个物体的质量相等

这时m₁－m₂＝0，m₁＋m₂＝2m₁。根据（1）、（2）两式，有

v₁ʹ＝0

v₂ʹ＝v₁

这表示第一个物体的速度由v₁变为零，而第二个物体由静止开始运动，运动的速度等于第一个物体原来的速度。

• 若m₁≫m₂，即第一个物体的质量比第二个物体大得多

这时m₁－m₂≈m₁，m₁＋m₂≈m₁。根据（1）、（2）两式，有

v₁ʹ＝v₁

v₂ʹ＝2v₁

这表示碰撞后第一个物体的速度没有改变，而第二个物体以2v₁的速度被撞出去。

• 若m₁≪m₂，即第一个物体的质量比第二个物体小得多

这时m₁－m₂≈－m₂，\(\frac{{2{m_1}}}{{{m_1} + {m_2}}}\)≈0。根据（1）、（2）两式，有

v₁ʹ＝－v₁

v₂ʹ＝0

这表示碰撞以后第一个物体被撞了回去，以原来的速率向反方向运动，而第二个物体仍然静止。

这里从理论上讨论了本章第1节开始时的实验。如果在这些讨论之后再做那个实验，你是不是对科学理论与实验的关系有些新的体验？

对心碰撞和非对心碰撞

如图16.4-3甲，一个运动的球与一个静止的球碰撞，碰撞之前球的运动速度与两球心的连线在同一条直线上，碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰（direct impact），也叫对心碰撞。

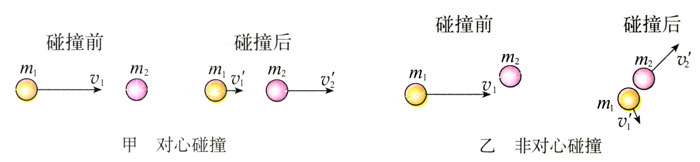
一个运动的球与一个静止的球碰撞，如果碰撞之前球的运动速度与两球心的连线不在同一条直线上，碰撞之后两球的速度都会偏离原来两球心的连线。这种碰撞称为非对心碰撞。

发生对心碰撞的两个物体，碰撞前后的速度都沿同一条直线，它们的动量也都沿这条直线，可以在这个方向上应用动量守恒定律。前面我们已经多次遇到这种情形。

发生非对心碰撞的两个物体，碰撞后的速度都不与原来的速度在同一条直线上，所以非对心碰撞比较复杂，是平面内的二维问题。

思考与讨论

如图16.4-4，A球以速度v₁与同样质量且处于静止的B球碰撞。已知碰撞后B球的速度如图所示，请你大致画出碰撞后A球的速度。

散射

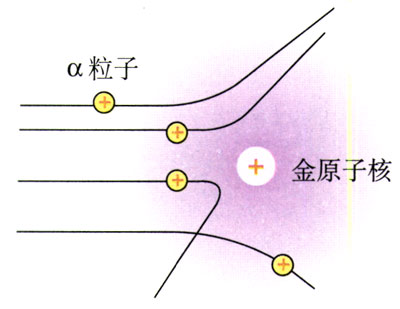
在粒子物理和核物理中，常常使一束粒子射入物体，粒子与物体中的微粒碰撞。研究碰撞后粒子的运动方向，可以得到与物质微观结构有关的很多信息。与宏观物体碰撞不同的是，微观粒子相互接近时并不发生直接接触，因此微观粒子的碰撞又叫做散射（scattering）。由于粒子与物质微粒发生对心碰撞的概率很小，所以多数粒子在碰撞后飞向四面八方。

科学足迹

中子的发现

1932年，物理学历史上发生了一个重要的事件——发现了中子。

早在1920年，在发现电子和质子之后不久，卢瑟福就猜测，原子中可能还有一种电中性的粒子。英国物理学家查德威克（J．Chadwick，1891～1974）在卡文迪许实验室里寻找这种电中性粒子。他一直在设法加速质子，用它撞击原子核，以发现有关中性粒子的证据。1929年，他用高速质子轰击了铍原子核。

实际上，德国物理学家博特及其合作者贝克尔已经先行一步。他们用α粒子轰击一系列元素，在轰击铍原子核时，产生了一种未知射线。为了确定这种射线的性质，他们试着把各种物体放在射线经过的路径上，结果发现这种射线的穿透能力极强，在穿透2 cm厚的铅板后强度只减弱30%。当时知道，能有这样强的穿透能力的只有γ射线。因此，他们认为这种射线是一种γ射线。

法国物理学家约里奥-居里夫妇重复了博特和贝克尔的实验。他们在铍板与测量仪器之间插入了石蜡，结果石蜡在这种“铍射线”的照射下会发出质子，而没有石蜡时射线是不带电的。但是，约里奥-居里夫妇认为石蜡被照射时产生质子是一种康普顿效应[1]，他们仍然认为中性的“铍射线”是一种γ射线。

查德威克认为新射线不可能是γ射线，因为一般情况下γ射线容易被密度大的物质吸收，但这种射线却不是这样。他还观察到一个新的现象：在用这种射线轰击氢核时，它能被反弹回来。通过对反冲核的动量的测定，再应用动量守恒定律进行估算，得知这种射线是由质量与质子大致相等的中性粒子组成。随后他于1932年在《自然》杂志上发表了《中子可能存在》的论文。

查德威克发现了12年前他的老师卢瑟福所预言的粒子——中子，为此，他获得了1935年的诺贝尔物理学奖。

博特发现了“铍辐射”却没有认识到它就是中子，多年以后他还深感遗憾。如果他们去听了卢瑟福的演讲，也许就不会失去这次重大发现，因为卢瑟福就是在那场演讲中谈到了自己对中子的猜想。

这是科学史上一个“真理碰到了鼻子还没有发现”的著名例子，它说明科学信息的交流与科学思想的碰撞是多么重要。

问题与练习

1．在气垫导轨上，一个质量为600 g的滑块以15 cm/s的速度与另一个质量为400 g、速度为10 cm/s方向相反的滑块迎面相撞，碰撞后两个滑块并在一起，求碰撞后滑块速度的大小和方向。

2．质量为m速度为v的A球跟质量为3m的静止B球发生正碰。碰撞可能是弹性的，也可能是非弹性的，因此，碰撞后B球的速度可能有不同的值。请你论证：碰撞后B球的速度可能是以下值吗？

（1）0.6v；（2）0.4v；（3）0.2v。

3．速度为10³ m/s的氦核与静止的质子发生正碰，氦核的质量是质子的4倍，碰撞是弹性的，求碰撞后两个粒子的速度。

4．有些核反应堆里要让中子与原子核碰撞，以便把中子的速率降下来。为此，应该选用质量较大的还是质量较小的原子核？为什么？

5．一种未知粒子跟静止的氢原子核正碰，测出碰撞后氢原子核的速度是3.3×10⁷m/s。该未知粒子跟静止的氮原子核正碰时，测出碰撞后氮原子核的速度是4.7×10⁶ m/s。已知氢原子核的质量是m_H，氮原子核的质量是14 m_H，上述碰撞都是弹性碰撞，求未知粒子的质量。这实际是历史上查德威克测量中子质量从而发现中子的实验，请你根据以上查德威克的实验数据计算：中子的质量与氢核的质量m_H有什么关系？

发布时间：2017/6/26 上午11:04:02  阅读次数：5209