第十六章 3 动量守恒定律（二）

动量守恒定律与牛顿运动定律

我们用牛顿运动定律分析两个小球的碰撞。可以看到，所得结论与动量守恒定律的结论相同。

如图16.3-1所示，在水平桌面上做匀速运动的两个小球，质量分别是m₁和m₂，沿着同一直线向相同的方向运动，速度分别是v₁和v₂，v₂>v₁。当第二个小球追上第一个小球时两球碰撞。碰撞后的速度分别是v₁ʹ和v₂ʹ。碰撞过程中第一个球所受第二个球对它的作用力是F₁，第二个球所受第一个球对它的作用力是F₂。

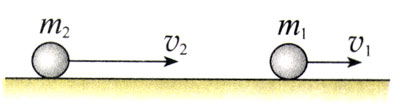
根据牛顿第二定律，碰撞过程中两球的加速度分别是

a₁＝\(\frac{{{F_1}}}{{{m_1}}}\)，a₂＝\(\frac{{{F_2}}}{{{m_2}}}\)

根据牛顿第三定律，F₁与F₂大小相等、方向相反，即

F₁=F₂

所以

m₁a₁=－m₂a₂

碰撞时两球之间力的作用时间很短，用Δt表示。这样，加速度与碰撞前后速度的关系就是

a₁＝\(\frac{{{v_1}^\prime - {v_1}}}{{\Delta t}}\)，a₂＝\(\frac{{{v_2}^\prime - {v_2}}}{{\Delta t}}\)

把加速度的表达式代入m₁a₁=－m₂a₂，移项后得到

m₁v₁+m₂v₂=m₁v₁′+m₂v₂′                （1）

它的物理意义是：两球碰撞前的动量之和等于碰撞后的动量之和。这个结果与动量守恒定律是一致的。

自然规律本身是和谐的。如果新的认识与过去的认识出现了矛盾，那么或者是我们的推理出现了错误，或者过去认识的规律在新环境下不适用了。

动量守恒定律的普适性

既然许多问题可以通过牛顿运动定律解决，为什么还要研究动量守恒定律？

从上面的例子可以看到，用牛顿运动定律解决问题要涉及整个过程中的力。有的时候，力的形式很复杂，甚至是变化的，解起来很复杂，甚至不能求解。但是动量守恒定律只涉及过程始末两个状态，与过程中力的细节无关。这样，问题往往能大大简化。

除此之外，两者还有更深刻的差别。近代物理的研究对象已经扩展到我们直接经验所不熟悉的高速（接近光速）、微观（小到分子、原子的尺度）领域。实验事实证明，在这些领域，牛顿运动定律不再适用，而动量守恒定律仍然正确。

电磁场是现代物理学的重要研究对象。在下一章我们会看到，电磁场的运动，即电磁波，也具有动量，它与粒子的相互作用也遵守动量守恒定律。

动量守恒定律是一个独立的实验规律，它适用于目前为止物理学研究的一切领域。随着学习的深入，同学们对此将有更深刻的体会。

【例题】一枚在空中飞行的导弹，质量为m，在某点的速度为v，方向水平。导弹在该点突然炸裂成两块（图16.3-2），其中质量为m₁的一块沿着与v相反的方向飞去，速度为v₁。求炸裂后另一块的速度v₂。

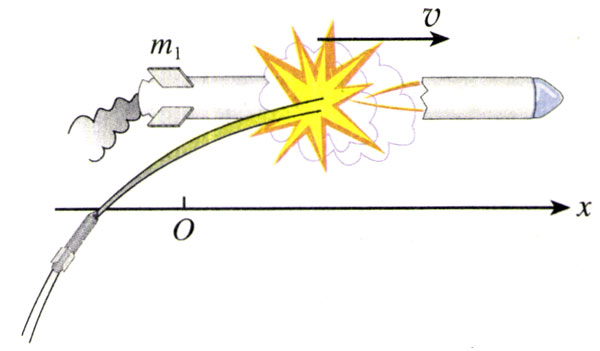
【分析】炸裂前，可以认为导弹是由质量为m₁和（m－m₁）的两部分组成，导弹的炸裂过程可以看做这两部分相互作用的过程。这两部分组成的系统是我们的研究对象。在炸裂过程中，炸裂成的两部分都受到重力的作用，所受外力的矢量和不为零，但是它们所受的重力远小于爆炸时燃气对它们的作用力，所以爆炸过程中重力的作用可以忽略，可以认为系统满足动量守恒定律的条件。

【解】导弹炸裂前的总动量为

p＝mv

炸裂后的总动量为

p′＝m₁v₁+（m－m₁）v₂

根据动量守恒定律p'=p，可得

m₁v₁+（m－m₁）v₂＝mv

解出

v₂＝\(\frac{{mv - {m_1}{v_1}}}{{m - {m_1}}}\)

若沿炸裂前速度v的方向建立坐标轴，v为正值；v₁与v的方向相反，v₁为负值。此外，一定有m－m₁>0。于是，由上式可知，v₂应为正值。这表示质量为（m－m₁）的那部分沿着与坐标轴相同的方向飞去。这个结论容易理解。炸裂的一部分沿着相反的方向飞去，另一部分不会也沿着相反的方向飞去，假如这样，炸裂后的总动量将与炸裂前的总动量方向相反，动量就不守恒了。

思考与讨论

如图16.3-3所示，一个质量是0.2 kg的钢球，以2m/s的速度斜射到坚硬的大理石板上，入射的角度是45°，碰撞后被斜着弹出，弹出的角度也是45°，速度仍为2 m/s。请你用作图的方法求出钢球动量变化的大小和方向。

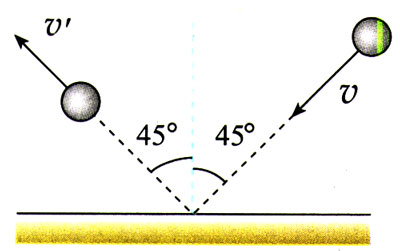
问题与练习

1．原来静止在滑冰场上的两个人，不论谁来推谁一下，两个人都会向相反方向滑去，他们的动量都发生了变化。两个人本来都没有动量，现在都有了动量，他们的动量变化服从什么规律？

2．质量为60 kg的运动员站在一艘质量是120 kg的小平板木船上。从某时刻开始，运动员开始从船头向船尾跑去，2s末到达船尾时获得了6m/s相对于河岸的水平速度。以下不考虑水的阻力。

（1）设运动员在这2s内的运动是匀加速直线运动，运动员受到的水平作用力是多大？

（2）这2s内运动员对船的水平作用力是多大？

（3）这2s内船倒退的加速度是多大？2s末船获得了多大的速度？

（4）不考虑运动员与船的相互作用过程的细节，请用动量守恒定律计算2s末船的速度。

（5）如果运动员与船的相互作用力是变力，船的速度还是第（4）小题计算的值吗？

（6）如果运功员在某一瞬时的速度是3 m/s，此时刻船的速度是多大？

3．在光滑的水平面上有一辆平板车，一个人站在车上用大锤敲打车的左端（图16.3-5）。在连续的敲打下，这辆车能持续地向右运动吗？说明理由。

4．A、B两个粒子都带正电，B的电荷量是A的2倍、B的质量是A的4倍。A以已知速度v向静止的B粒子飞去。由于库仑斥力，它们之间的距离缩短到某一极限值后又被弹开，然后各自以新的速度做匀速直线运动。设作用前后它们的轨迹都在同一直线上，请在以上提供的信息中选择有用的已知条件，计算当A、B之间的距离最近时它们各自的速度。

5．某机车以0.8 m/s的速度驶向停在铁轨上的15节车厢，跟它们对接。机车跟第一节车厢相碰后，它们连在一起具有一个共同的速度，紧接着又跟第二节车厢相碰，就这样，直至碰上最后一节车厢。设机车和车厢的质量都相等，求：跟最后一节车厢碰撞后车厢的速度。铁轨的摩擦忽略不计。

6．甲、乙两物体沿同一直线相向运动，甲物体的速度是6 m/s，乙物体的速度是2m/s。碰撞后两物体都沿各自原方向的反方向运动，速度都是4 m/s。求甲、乙两物体的质量之比。

7．在细线下吊着一个质量为m₁的沙袋，构成一个单摆，摆长为l。一颗质量为m的子弹水平射入沙袋并留在沙袋中，随沙袋一起摆动。已知沙袋摆动时摆线的最大偏角是θ，求子弹射入沙袋前的速度。

发布时间：2017/6/23 下午10:06:42  阅读次数：2083