第十六章 2 动量守恒定律（一）

动量

上节的探究使我们看到，不论哪一种形式的碰撞，碰撞前后两个物体mv的矢量和保持不变。其他实验和观察到的事实也都得出同样的结论。这就给我们一个启示：mv很可能具有特别的物理意义。物理学中把它定义为动量（momentum），用字母p表示

p=mv

科学前辈就是在追寻不变量的努力中，逐渐明确了动量的概念。

最先提出动量具有守恒性思想的是法国科学家笛卡儿（R．Descartes，1596 -1650）。他继承了伽利略的说法，把物体的大小（质量）与速率的乘积叫做动量，并认为它是量度运动的唯一正确的物理量。然而，笛卡儿忽略了动量的方向性。尽管如此，他的工作还是给后来人的继续探索打下了很好的基础。

1668年，惠更斯发表了一篇题为《关于碰撞对物体运动的影响》的论文，总结了他对碰撞问题的实验和理论研究。结论是：“每个物体所具有的‘动量’在碰撞时可以增多或减少，但是它们的量值在同一个方向的总和却保持不变，如果减去反方向运动的话。”他在这里明确指出了动量的方向性和守恒性，可以认为是动量守恒关系的最初表述。

牛顿把笛卡儿的定义做了修改，即不用质量与速率的乘积：而明确地用质量与速度的乘积定义动量。这样就可以更清楚地表述动量的方向性及其守恒关系。

由于速度是矢量，所以动量也是矢量，它的方向与速度的方向相同。

【例题1】

一个质量是0.1 kg的钢球，以6m/s的速度水平向右运动，碰到一个坚硬的障碍物后被弹回，沿着同一直线以6 m/s的速度水平向左运动（图16.2-1），碰撞前后钢琴的动量各是多少？碰撞前后钢球的动量变化了多少？

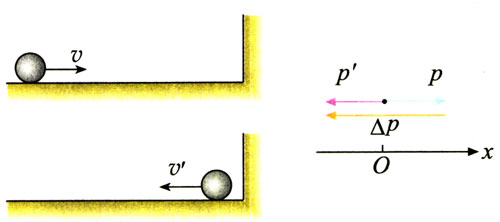
【分析】动量是矢量，虽然碰撞前后钢球速度的大小没有变化，都是6 m/s，但速度的方向变化了，所以动量的方向也发生了变化。也就是说，碰撞前后的动量并不相同。

为了求得钢球动量的变化量，先要确定碰撞前和碰撞后钢球的动量。碰撞前后钢球是在同一条直线上运动的。选定坐标轴的方向，例如，取水平向右的方向为坐标轴的方向。碰撞前钢球的运动方向与坐标轴的方向相同，动量为正值；碰撞后钢球的运动方向与坐标轴的方向相反，动量为负值。钢球动量的变化等于碰撞后的动量减去碰撞前的动量。

【解】取水平向右的方向为坐标轴的方向。碰撞前钢球的速度v=6 m/s，碰撞前钢球的动量为

p=mv=0.1×6 kg·m/s=0.6 kg·m/s

碰撞后钢球的速度vʹ=-6 m/s，碰撞后钢球动量为

pʹ=mvʹ=－0.1×6 kg·m/s=－0.6 kg·m/s

碰撞前后钢球动量的变化为

Δp=pʹ－p=（－0.6-0.6）kg·m/s=-1.2 kg·m/s

动量的变化Δp是矢量，求得的数值为负值，表示Δp的方向与坐标轴的方向相反，即Δp的方向水平向左。

系统 内力和外力

上节实验研究的是碰撞。与过去研究的大多数力学问题不同，碰撞的研究对象不是一个物体，而是两个（或多个）物体。我们说这两个（或多个）物体组成了一个力学系统（system）。实际上过去我们也曾涉及系统的问题。例如，重力势能属于地面附近的物体与地球组成的系统；轻质弹簧产生的弹性势能属于它所连接的两个物体。在碰撞问题中，研究炸弹的爆炸时，它的所有碎片及产生的燃气也要作为一个系统来处理。

碰撞时两个物体之间一定有相互作用力，由于这两个物体是属于同一系统的，它们之间的力叫做内力（internal force）。两个物体还会受到重力，如果放到桌面上，它们还会受到桌面的支持力、摩擦力。这些力是系统以外的物体施加的，叫做外力（external force）。

动量守恒定律

经过几代物理学家的探索写争论，人们在18世纪形成了这样的共识：如果一个系统不受外力，或者所受外力的矢量和为零，这个系统的总动量保持不变。这就是动量守恒定律（law of conservation of momentum）。

为了正确认识动量守恒定律，需要注意以下几点。

1．区分内力和外力

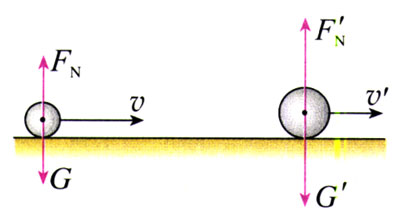
以在光滑水平桌面上发生碰撞的两个物体为例，它们之间一定有相互作用，这是内力；它们还要受到重力和桌面对它们的支持力，这是外力。水平桌面上的每个物体所受的重力与它所受的支持力都是大小相等、方向相反的，矢量和为零，因此系统所受的外力的矢量和为零。光滑水平桌面上两个物体碰撞的问题符合动量守恒定律的条件。

2．在总动量一定的情况下，每个物体的动量可以发生很大的变化

例如，静止的两辆小车用细线相连，中间有一个压缩了的弹簧（图16.2-4）。烧断细线后，由于弹力的作用，两辆小车分别向左右运动，它们都获得了动量，但动量的矢量和仍然是零。

【例题2】在列车编组站里，一辆m₁＝1.8×10⁴ kg的货车在平直轨道上以v₁＝2 m/s的速度运动，碰上一辆m₂=2.2×10⁴ kg的静止的货车，它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。

【分析】两辆货车在碰撞过程中发生相互作用，它们是一个系统，这个系统是我们的研究对象。系统所受的外力有：重力、地面支持力、地面摩擦力和空气阻力。重力与支持力之和等于零，摩擦力和空气阻力远小于碰撞过程中发生的内力，可以忽略。因此，可以认为碰撞过程中系统所受外力的矢量和为零，动量守恒。

为了应用动量守恒定律解决这个问题，需要确定碰撞前后的动量。碰撞前的动量是指即将发生碰撞那一时刻的动量，而不是指发生碰撞之前若干时间以前的动量；碰撞后的动量是指碰撞刚结束那一时刻的动量，而不是指碰撞结束若干时间之后的动量。

分析物理现象不但要明确研究列象，而且要明确研究的是哪一段过程。也就是说，要明确哪个状态是我们研究的过程的初状态，哪个是过程的末状态，初状态是开始相互作用时的状态，末状态是相互作用结束时的状态。

【解】沿碰撞前货车运动的方向建立坐标轴（图16.2-5），则有v₁=2 m/s。设两车结合后的速度为v。两车碰撞前的总动量为

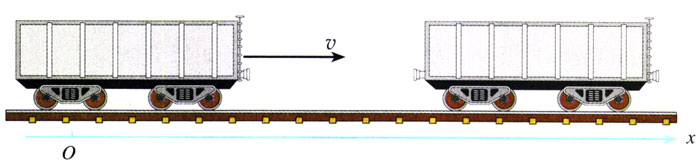
p=m₁v₁

碰撞后的总动量为

pʹ=(m₁+m₂)v

由动量守恒定律pʹ=p可得

m₁v₁=(m₁+m₂)v

所以

v=\(\frac{{{m_1}{v_1}}}{{{m_1} + {m_2}}}\)

代入数值，得

v=0.9 m/s

两车结合后速度的大小是0.9 m/s；v是正值，表示结合后仍然向右运动。

问题与练习

1．解答以下三个小题，思考动量与动能的区别。

（1）质量为2 kg的物体，速度由3 m/s增大为6 m/s，它的动量和动能各增大为原来的几倍？

（2）质量为2 kg的物体，速度由向东的3 m/s变为向西的3 m/s，它的动量和动能是否变化了？如果变化了，变化量各是多少？

（3）A物体质量是2 kg，速度是3 m/s，方向向东；B物体质量是3 kg，速度是4m/s，方向向西。它们的动量之和是多少？动能之和是多少？

解答后做个小结，说说动量与动能有什么不同。以后的学习中还会学到动量与动能的区别，请注意及时总结。

2．甲、乙两位同学静止在光滑的冰面上，甲推了乙一下，结果两人向相反方向滑去。甲推乙前，他们的总动量为零。甲推乙后，他们都有了动量，总动量还等于零吗？已知甲的质量为50 kg，乙的质量为45 kg，甲的速率与乙的速率之比是多大？

3．A、B两个物体在同一直线上沿同一方向运动，A的质量是5 kg，速度是9m/s，B的质量是2 kg．速度是6m/s。A从后面追上B，它们相互作用一段时间后，B的速度增大为10 m/s，方向不变，这时A的速度是多大？方向如何？以上过程中除A、B两物体的相互作用力外，其他的力可以忽略。

4．质量是10 g的子弹，以300 m/s的速度射入质量是24 g、静止在光滑水平桌面上的木块，并留在木块中。子弹留在木块中以后，木块运动的速度是多大？如果子弹把木块打穿，子弹穿过后的速度为100 m/s，这时木块的速度又是多大？

发布时间：2017/6/22 下午1:12:08  阅读次数：3295