第十六章 1 实验:探究碰撞中的不变量
想像远比知识重要,知识有涯,而想像能环抱整个世界。
——爱因斯坦
台球的碰撞、火箭的起飞、微观粒子的散射,这些运动似乎有天壤之别。然而,物理学的研究表明,它们遵从相同的科学规律——动量守恒定律。动量守恒定律是自然界中最普遍的规律之一,无论是设计火箭还是研究微观粒子,都离不开它。
第十六章 1 实验:探究碰撞中的不变量
碰撞是自然界中常见的现象。两节火车车厢之间的挂钩靠碰撞连接,台球由于碰撞而改变运动状态,微观粒子之间更是由于相互碰撞而改变能量甚至使得一种粒子转化为其他粒子。
演示
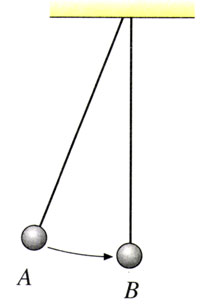
如图16.1-1,A、B是两个悬挂起来的钢球,质量相等。使B球静止,拉起A球,放开后A与B碰撞,观察碰撞前后两球运动的变化。
换成质量相差较多的两个小球,重做以上实验。
两个物体碰撞前后的速度都会发生变化,物体的质量不同时速度变化的情况也不一样。那么,碰撞前后会不会有什么物理量保持不变?
下面通过实验研究这个问题。
物理学家始终在寻求自然界万物运动的规律。其中包括在多变的世界里找出某些不变性。在《必修2》的第七章中我们曾经经历过这样的探究过程。
实验的基本思路
我们只研究最简单的情况——两个物体碰撞前沿同一直线运动,碰撞后仍沿这条直线运动。这种碰撞叫做一维碰撞。
与物体运动有关的物理量可能有哪些呢?在一维碰撞的情况下只有物体的质量和速度。设两个物体的质量分别为m1、m2,碰撞前的速度分别为v1、v2,碰撞后的速度分别为v1ʹ、v2ʹ,如果速度与我们设定的方向一致,取正值,否则取负值。
现在的问题是,碰撞前后哪个物理量可能是不变的?质量是不变的,但质量并不描述物体的运动状态,不是我们追寻的“不变量”。速度在碰撞前后是变化的,但一个物体的质量与它的速度的乘积是不是不变量?如果不是,那么,两个物体各自的质量与自己的速度的乘积之和是不是不变量?也就是说,关系式
m1v1+m2v2=m1v1ʹ+m2v2ʹ
是否成立?
如果左式成立,那就表示“m1v1+m2v2”是碰撞前后的不变量。
或者,各自的质量与自己的速度的二次方的乘积之和是不变量?也就是说,关系式
m1v12+m2v22=m1v1ʹ2+m2v2ʹ2
是否成立?
也许,两个物体的速度与自己质量的比值之和在碰撞前后保持不变?也就是说,关系式
\(\frac{{{v_1}}}{{{m_1}}}\)+\(\frac{{{v_2}}}{{{m_2}}}\)=\(\frac{{{{v'}_1}}}{{{m_1}}}\)+\(\frac{{{{v'}_2}}}{{{m_2}}}\)
是否成立?
也许……
碰撞可能有很多情形。例如两个物体可能碰后分开,也可能粘在一起不再分开……我们寻找的不变量必须在各种碰撞的情况下都不改变,这样才符合要求。
需要考虑的问题
实验中首要的问题是如何保证碰撞是一维的,即如何保证两个物体在碰撞之前沿同一直线运动,碰撞之后还沿这条直线运动。此外,还要考虑怎样测量物体的质量、怎样测量两个物体在碰撞前后的速度。
质量可以用天平测量,所以,本实验要解决的主要问题是怎样保证物体沿同一直线运动和怎样测量物体的速度。
关于实验数据的处理,下面的表格可供参考。填表时应注意思考:如果小球碰撞后运功的速度与原来的方向相反,应该怎样记录?
|
|
碰撞前 |
碰撞后 |
||
|
质量 |
m1 |
m2 |
m1 |
m2 |
|
速度 |
v1 |
v2 |
v1ʹ |
v2ʹ |
|
mv |
m1v1+m2v2 |
m1v1ʹ+m2v2ʹ |
||
|
mv2 |
m1v12+m2v22 |
m1v1ʹ2+m2v2ʹ2 |
||
|
|
\(\frac{{{v_1}}}{{{m_1}}}\)+\(\frac{{{v_2}}}{{{m_2}}}\) |
\(\frac{{{{v'}_1}}}{{{m_1}}}\)+\(\frac{{{{v'}_2}}}{{{m_2}}}\) |
||
|
… |
… |
… |
||
对于每一种碰撞的情况(例如两个物体碰后分开或粘在一起的两种情况),都要填写一个类似的表格,然后根据表中的数据寻找碰撞前后的不变量。举例来说,如果每个表格中\(\frac{v}{m}\)那一行第二列和第三列的求和的值都相等,那么\(\frac{{{v_1}}}{{{m_1}}}\)+\(\frac{{{v_2}}}{{{m_2}}}\)可能就是我们寻找的不变量。
参考案例一
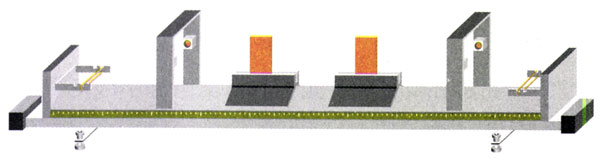
《必修1》第一章介绍了气垫导轨和光电计时装置的工作原理。利用气垫导轨能够很容易地保证两个滑块的碰撞是一维的。与之配套的光电计时装置可以迅速测量两个滑块碰撞前后的速度。
实验装置如图16.1-2所示。不同的质量可以通过在滑块上加重物的办法实现。应用气垫导轨很容易控制滑块碰撞前的速度或使它在碰撞前静止。因此,这个方案是本实验的首选。
还有两点值得注意。
1.原来连在一起的两个物体,由于相互之间具有排斥的力而分开,这实际上也是一种碰撞。这种情况可以通过下面的方法实现。
用细线将弹簧片拉成弓形,放在两个滑块之间,并使它们静止。然后烧断细弹簧片弹开后落下,两个滑块随即向相反方向运动(图16.1-3甲)。
2.碰撞时难免有能量损失。只有当某个物理量在能量损失较大和损失较小的碰撞中都不变,它才有可能是我们寻找的不变量。
在两滑块相碰的端面装上弹性碰撞架(图16.1-3乙),可以得到能量损失很小的碰撞。在滑块的碰撞端贴胶布,可以增大碰撞时的能量损失。如果在两个滑块的碰撞端分别装上撞针和橡皮泥(图16.1-3丙),碰撞时撞针插入橡皮泥中,把两个滑块连接成一体运动,这样的碰撞中能量损失很大(有兴趣的同学不难通过实验证明这一点)。如果在两个滑块的碰撞端分别贴上尼龙拉扣,碰撞时它们也会连成一体。

参考案例二
实验装置如图16.1-4所示。
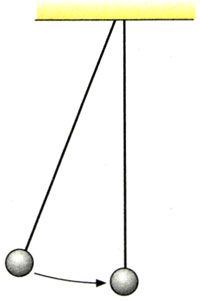
把两个小球用线悬起来,一个小球静止,拉起另一个小球,放下时它们相碰。
可以测量小球被拉起的角度,从而算出落下时的速度;测量被撞小球摆起的角度,从而算出被撞后的速度。
也可以用贴胶布等方法增大两球碰撞时的能量损失。
参考案例三
将打点计时器固定在光滑桌面的一端,把纸带穿过打点计时器,连在小车A的后面。让小车A运动,小车B静止。在两小车的碰撞端分别装上撞针和橡皮泥(图16.1-5),碰撞时撞针插入橡皮泥中,把两个小车连接成一体。通过纸带测出它们碰撞前后的速度。

通过这个实验,你是否找到了碰撞前后的“不变量”?即使找到了,它也仍然带有猜想的性质,但你对自己的猜想会增加几分把握。只有根据实验结果推导出的许许多多新结论都与事实一致时,猜想才能成为一条定律。尽管如此,本节实验还是很有意义的,它让我们再一次体验了探究自然规律的过程。
问题与练习
1.光滑桌面上有1、2两个小球。1球的质量为0.3 kg,以8 m/s的速度跟质量为0.1 kg的静止的2球碰撞,碰撞后2球的速度变为9 m/s,1球的速度变为5m/s,方向与原来相同。根据这些实验数据,晓明对这次碰撞的规律做了如下几项猜想。
(1)碰撞后2球获得了速度,是否是1球把速度传递给了2球?经计算,2球增加的速度是9 m/s,1球减小的速度是3 m/s,因此,这种猜想不成立。
(2)碰撞后2球获得了动能,是否是1球把动能传递给了2球?经计算,2球增加的动能是4.05 J,1球减小的动能是5.85 J,这种猜想也不成立。
(3)请你根据实验数据猜想:有一个什么物理量,在这次碰撞中2球所增加的这个量与1球所减小的这个量相等?通过计算说明。
2.水平光滑桌面上有A、B两个小车,质量都是0.6 kg。A车的车尾连着一个打点计时器的纸带,A车以某一速度与静止的B车碰撞,碰后两车连在一起共同向前运动。碰撞前后打点计时器打下的纸带如图16.1-6所示。根据这些数据,请猜想:把两个小车加在一起计算,有一个什么物理量在碰撞前后可能是相等的?

发布时间:2017/6/21 下午1:46:03 阅读次数:2512
