第十五章 2 时间和空间的相对性

“同时”的相对性

作为相对论的两个假设的直接推论，现在讨论“同时”的相对性，以体会相对论描述的世界与我们日常的经验有多大的差别。

先研究两个“事件”的同时性。在这里，“事件”可以指一个电子与观测仪器的碰撞，也可以指闪电对地面的打击，还可以指一个婴儿的诞生……在数学上，一个事件表示为空间和时间的一组坐标（x，y，z，t）。

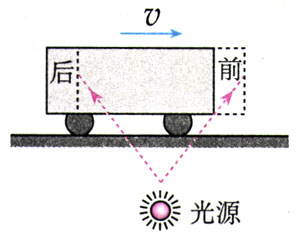
假设一列火车在沿平直轨道飞快地匀速行驶。车厢中央的光源发出了一个闪光，闪光照到了车厢的前壁和后壁，这是两个事件。车上的观察者认为两个事件是同时的。在他看来这很好解释，因为车厢是个惯性系，光向前、后传播的速度相同，光源又在车厢的中央，闪光当然会同时到达前后两壁（图15.2-1甲）。

车下的观察者不以为然。他观测到，闪光先到达后壁，后到达前壁。他的解释是：地面也是一个惯性系，闪光向前、后传播的速度对地面也是相同的，但是在闪光飞向两壁的过程中，车厢向前行进了一段距离，所以向前的光传播的路程长些，到达前壁的时刻也就晚些（图15.2-1乙），这两个事件不同时。

车上车下两位观察者推理的根据相同，都是狭义相对论的两个假设：他们都认为在自己的参考系中闪光向前、向后传播的速度是一样的；他们都认为“时间=\(\frac{距离}{速度}\)”这个公式是正确的。他们谁都没有错。

在经典物理学家的头脑中，如果两个事件在一个参考系中是同时的，在另一个参考系中一定也是同时的，这一点似乎天经地义，无需讨论。但是，如果接受了爱因斯坦的两个假设，我们自然会得出“同时是相对的”这样一个结论。为什么在日常生活中没有人觉察到这种相对性？原来，火车运动的速度远远小于光速，光从车厢中央传播到前后两壁的短暂时间内，火车前进不了多大距离，因此地面观察者不会发现闪光到达前壁、后壁的时间差。

思考与讨论

与图15.2-1的例子相似，列车K的某车厢的中央发出了一个闪光，车厢中的人认为闪光同时到达了前后两壁（事件A和B）。不同的是，列车K静止在车站里，另一列火车L从旁边呼啸而过（图15.2-2）。那么，在运动的火车L里，观察者认为，沿着运动方向位置靠前一些的事件A先发生，还是靠后一些的事件B先发生？

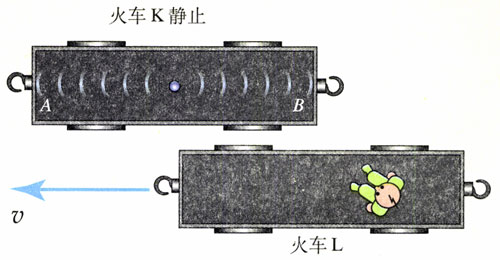
考虑这个问题时可以仿照讨论图15.2-1的思路，也可以直接应用图15.2-1问题的结论，只是认为地面在相对于火车L运动。

暂时记住这个结论，讨论下面的问题会方便些。

长度的相对性

经典物理学家认为，一条杆的长度不会因为观察者是否与杆做相对运动而不同。但是下面的分析表明，杆的长度的确与观察者和杆之间的相对运动有关。

假设杆MN沿着车厢运动的方向固定在火车上（图15.2-3），与车一起运动。火车上的观察者认为杆是静止的。他利用固定在火车上的坐标轴，读出杆的两端M、N的位置坐标，坐标之差就是他测出的杆长lʹ。地面观察者利用固定在地面上的坐标轴，读出杆两端的位置坐标，坐标之差就是他测出的杆长l。不过，地面观察者读数时要谨慎，因为对他来说杆是运动的，要使这种测量有意义，他必须同时读出M、N两点的坐标。

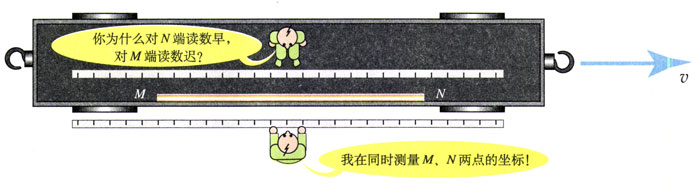
然而，火车上的观察者会怎样评论地面观察者的测量过程呢？我们已经认识到，由于同时的相对性，尽管地面观察者认为自己对M、N两端的读数是同时的，但火车上的观察者认为他对两端的读数不是同时的。根据上面“思考与讨论”的结论，火车上的观察者认为，地面观察者先在N点读数，而后才在M点读数，在这期间杆已经相对地面向前运动了一截！因此火车上的观察者断定，地面观察着测得的杆长会比自己测得的数值小一些。

讨论这个问题时要记住：杆固定在车厢中，它相对于车上的观察者是静止的。

通过严格的数学推导可以得到，如果与杆相对静止的人认为杆长是l₀，与杆相对运动的人认为杆长是l，那么两者之间的关系是

l＝l₀\(\sqrt {1 - {{\left( {\frac{v}{c}} \right)}^2}} \)                               （1）

由于\({\left( {\frac{v}{c}} \right)^2}\)<1，所以总有l<l₀，即与杆相对运动的人观察到的杆长l总小于与杆相对静止的人观察到的杆长l₀。一条沿自身长度方向运动的杆，其长度总比杆静止时的长度小。严格的数学推导还表明，在垂直于运动方向上，杆的长度没有变化。

可以想像这样一幅图景：一列火车以接近光的速度从我们身边飞驶而过，我们测得车厢前后壁的距离变小了，车窗变窄了……火车越快，这个现象越明显，但是车厢和车窗的高度都没有变化。车上的人有什么感觉呢？他认为车上的一切都与往常一样，因为他与火车是相对静止的。但是，他对地面景物测量的结果却有些异常：沿铁路电线杆的距离变短了，面对铁路的正方形布告牌由于宽度变小而高度未变竟成了窄而高的矩形[1]……车上的人和车下的人谁说得对？都对。这就好像相向行走的两个人，一个说小桥在左边，另一个说小桥在右边。

车辆、飞机等常见物体的运动速度v远远小于光速c，\({\left( {\frac{v}{c}} \right)^2}\)≈1，所以日常生活中观察不到长度的相对性。

特别需要指出的是，这种长度的变短是相对的。如果两条平行的、相同的杆在沿自己的

长度方向做相对运动，与它们一起运动的两位观察者都会认为对方的杆比自己的杆短一些。

时间间隔的相对性

经典物理学认为，某两个事件，在不同的惯性参考系中观察，它们的时间间隔总是相同的。例如，一个单摆从一端摆到另一端，守候在旁进行实验的人测得所用的时间是1 s，那么乘坐飞机经过实验室上空的人测得的时间间隔一定也是1 s。但是，在相对论物理学看来，两者测得的时间并不一样。

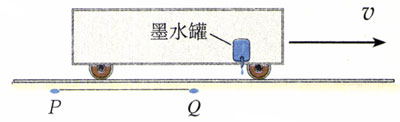
还以高速列车为例（图15.2-4）。假定车厢安装着一个墨水罐，它每隔一定时间滴出一滴墨水。车上的人测得，墨水在t₁ʹ、t₂ʹ两个时刻在地面形成P、Q两个墨点，也就是说发生了两个事件。车上的人认为两个事件的时间间隔是

Δτ=t₂ʹ－t₁ʹ

地面观察者洌得的时间间隔为

Δt=t₂－t₁

根据（1）式，通过一定的数学推导可以得到

Δt＝\(\frac{{\Delta \tau }}{{\sqrt {1 - {{\left( {\frac{v}{c}} \right)}^2}} }}\)                  （2）

Δτ是与墨水罐相对静止的观察者测得的两次滴下墨汁的时间间隔。

（2）式具有普遍意义。可以设想，飞船上有一只表，在航天员看来，表针走过一个小格所用的时间为Δτ。飞船与地面的相对速度是v，根据（2）式，地面的人认为表针走过一个小格的时间为Δt，比Δτ大。

从地面上观察，飞船上的时间进程比地面上慢。由于飞船在运动，船上的一切物理、化学过程和生命过程都变慢了：时钟走得慢了，化学反应慢了，甚至人的动作、人的新陈代谢也变慢了……可是飞船上的人自己没有这种感觉，他们反而认为地面上的时间进程比飞船上的慢，因为他们看到，地面正以同样的速度朝相反的方向运动！

时空相对性的验证

从（1）、（2）两式可以看到，只有当两个参考系的相对速度v可与光速c相比时，时间和空间的相对性才比较明显。目前的技术还不能使宏观物体达到这样的速度。但是随着对微观粒子研究的不断深入，人们发现，许多情况下粒子的速度会达到光速的90%以上，时空的相对性应该是不可忽略的。事实正是如此。时至今日，不但狭义相对论的所有结论已经完全得到证实，而且它已经成为微观粒子研究的基础之一。

时空相对性的最早证据跟宇宙线的观测有关。原始宇宙线是来自太阳和宇宙深处的高能粒子流，它与大气作用，又产生多种粒子，叫做次级宇宙线。次级宇宙线中有一种粒子叫做μ子，寿命不长，生成之后很快就衰变为别的粒子。

原始宇宙线在高至几百千米、低至十几千米的高度都能与大气中的粒子作用产生μ子，μ子的速度、寿命各不相同，因此在不同高度都能在宇宙线中观测到μ子。根据牛顿力学和统计物理学可以算出μ子的数量随高度变化的情况，但是实际观测到的μ子的数量大于经典理论做出的预言。这只能用狭义相对论做如下解释。

在实验室中测量，μ子低速运动时的平均寿命是3.0 μs，但宇宙线中的μ子以0.99 c甚至更高的速度飞行，这种情况下再在地面上测量，它的平均寿命就远大于3.0 μs了。因此，在地面上观察，它将飞行较长的距离才会转变为其他粒子。

如果观察者与μ子一起运动，这个现象也好解释。这位观察者认为μ子的平均寿命仍是3.0 μs，但是大地正向他扑面而来，因此大气层的厚度比地面上的测量值小得多，μ子在短短的寿命中可以达到更接近地面的位置。

1941年美国科学家罗西和霍尔做这项研究时在不同高度统计了宇宙线中μ子的数量，结果与相对论的预言完全一致。

相对论的第一次宏观验证是在1971年进行的。当时在地面上将四只铯原子钟调整同步，然后把它们分别放在两架喷气式飞机上做环球飞行，一架向东飞，另一架向西飞。两架飞机各绕地球飞行一周后回到地面，与留在地面上的铯原子钟进行比较。实验结果与相对论的理论预言符合得很好。[2]

相对论的时空观

什么是时间？什么是空间？时间和空间有什么性质？经典物理学对这些问题并没有正面问答。但是从它对问题的处理上，我们体会到，经典物理学认为空间好像一个盒子，一个没有边界的盒子，它是物质运动的场所。至于某一时刻在某一空间区域是否有物质存在，物质在做什么样的运动，这些对于空间本身没有影响，就像盒子里是否装了东西对于盒子的性质没有影响一样。时间与此相似，它在一分一秒地流逝，与物质的运动无关。换句话说，经典物理学认为空间和时间是脱离物质而存在的，是绝对的，空间与时间之间也是没有联系的。

相对论则认为空间和时间与物质的运动状态有关。前面已经看到，在一个确定的参考系中观察，运动物体的长度（空间距离）和它上面物理过程的快慢（时间进程）都跟物体的运动状态有关。

我们生活在低速运动的世界里，因此自然而然地接受了经典的时空观，过去谁都未曾有意识地考虑过空间与时间的性质。只有当新的实验事实引出的结论与传统观念不一致时，人们才回过头来认真思考过去对于空间和时间的认识。科学的发展和人类对于自然的认识就是这样一步一步地前进的。新科学没有全盘否定经典物理学，经典物理学的结论受到了无数次实践的检验。虽然相对论更具有普遍性，但是经典物理学作为相对论在低速运动时的特例，在自己的适用范围内还将继续发挥作用。

科学足迹

狭义相对论出现的前夜

19世纪末，对于物理学来说，大有“山雨欲来风满楼之势”。许许多多实验和理论的研究，已经使狭义相对论呼之欲出了。

麦克斯韦的电磁理论取得的成就不容置疑，为了使它能与新的实验事实相协调，特别是为了解释麦克耳孙实验和其他有关光速的实验，很多科学家试图修正以太理论。其中最有成效的是荷兰物理学家洛伦兹。他试图利用物体通过以太时以太的“收缩”来解释实验的结果，并且得到了相应的公式。狭义相对论中非常重要的坐标变换公式甚至就是以洛伦兹命名的。然而，他的思想仍被“以太”这个物化的绝对时空所束缚，未能建立新物理学的框架。

在想要创建新理论的科学家中，法国数学家、物理学家庞加莱走到了前面。1895年，他首次提出了相对性原理的思想。他认为，“要证明物质的绝对运动，或者更明确地说，要证明物质相对于以太的运动是不可能的”。1899年，他又进一步提出，“对于所有观察者来说，光速都是常数”，并强调了这一假设的必要性。庞加莱还论证了“两个事件历时相等”和“在两地同时发生的两个事件”的说法是没有意义的。与洛伦兹一样，庞加莱已经十分接近狭义相对论了。

1904年，就在爱因斯坦发表相对论的前一年，庞加莱在数学上给出了洛伦兹变换的更简捷的形式并正式命名为洛伦兹变换。他还通过论证指出，惯性应该随速度的增大而增大。他还指出，原有的力学只是新力学在一定条件下的近似。“相对性原理”一词也是庞加莱首先使用的。然而，尽管他的很多天才预见后来都被证明与爱因斯坦的相对论是一致的，他自己却找不到合适的方案来把这些预见放到一个逻辑体系中。

如果没有爱因斯坦，其他人也会建立狭义相对论，我们仍然能够享受到它所带来的进步。正如爱因斯坦本人在一封信中所写的那样：“毫无疑问，如果我们从回顾中去看狭义相对论的发展，那么它在1905年已经到了发现的成熟阶段。洛伦兹已经注意到，为了分析麦克斯韦方程，那些后来以他的名字而闻名的变换是重要的；庞加莱在有些方面甚至更深入了一步。”

问题与练习

1．地面上的人认为A、B两个事件同时发生。对于坐在火箭中沿两个事件发生地点连线飞行的人来说（图15.2-5），哪个事件先发生？

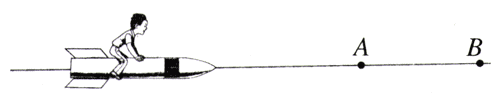
2．一列火车以速度v相对地面运动（图15.2-6），如果地面上的人测得，某光源发出的闪光同时到达车厢的前壁和后壁，那么按照火车上的人的测量，闪光是先到达前壁还是后壁？火车上的人怎样解释自己的测量结果？

3．一枚静止时长30 m的火箭以3 km/s的速度从观察者的身边掠过，观察者测得火箭的长度应为多少？火箭上的人测得火箭的长度应为多少？如果火箭的速度为光速的二分之一呢？

4．A、B、C是三个完全相同的时钟，A放在地面上，B、C分别放在两个火箭上．以速度v_b和v_c朝同一方向飞行，v_b<v_c。地面上的观察者认为哪个时钟走得最慢？哪个走得最快？

5．以8 km/s的速度运行的人造卫星上，一只完好的手表走过了1 min，地面上的人认为它走过这1 min“实际”花了多少时间？通过这个题目我们可以看到，即使对于人造卫星的飞快速度，相对论效应也是微不足道的。

发布时间：2017/6/15 上午9:32:48  阅读次数：1347