第十章 5 热力学第二定律的微观解释

热力学定律是以宏观事实为基础的，它告诉我们热学现象、热学过程遵循什么规律。但是，通过前面几章的学习我们已经知道，系统的宏观表现源于组成系统的微观粒子的统计规律。本节就要从微观的角度说明为什么涉及热运动的宏观过程会有一定的方向性。

有序和无序宏观态和微观态

生活中我们常说到有序和无序这两个词。一副扑克牌，按黑桃、红桃、梅花、方块的顺序，而且从小到大排列，我们说它是有序的，洗牌之后有序变成了无序。当然也可以规定奇数牌在先，偶数牌在后，等等。只要确定了某种规则，符合这个规则的就是有序的。由许多单张纸牌组成的系统，如果对个体的分布没有确定的要求，“怎样分布都可以”，我们就说这样的分布是无序的。

有序与无序是相对的。一副扑克牌，指定按黑桃、红桃、梅花、方块的顺序排列，但对号码的大小不做要求，这样的排列对于完全杂乱的一副牌来说是有序的，但对于不仅有花样方面的要求，而且对号码顺序也有要求的排列来说，就是无序的了。这就涉及有序程度的问题。

如果规定了扑克牌的花样顺序与号码顺序，借用统计物理学的术语来说，我们就是规定了一个“宏观态”。这时可能的排列方式只有一种。如果我们宽容一些，只规定花样的先后，号码的顺序可以任意，我们就是规定了另外一个“宏观态”。由于在符合花样先后的情况下不同的号码还可以有不同的排列，我们说这样的“宏观态”对座了好几个“微观态”。如果对花样先后和号码的顺序都不做规定，这也是一个“宏观态”，这个“宏观态”对应的“微观态”就更多了。

如果一个“宏观态”对应的“微观态”比较多，就说这个“宏观态”是比较无序的。

气体向真空的扩散

我们以气体向真空的扩散为例，说明宏观自发过程的方向性。

一个箱子被挡板分为左、右两室，左室有气体，右室为真空。撤去挡板后气体要由左向右扩散。我们将从分子热运动的角度分析这个过程的方向性。为了简单，假定气体只由A、B、C、D共4个分子组成。

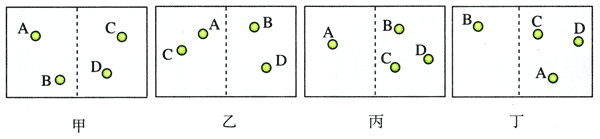
撤去挡板后每个分子都可以处于箱中任何位置，就像队列解散后的学生一样。如果细致地区分哪个分子在哪侧，这样一个一个的状态就是不同的微观态。例如，“A、B在左室，C、D在右室”与“A、C在左室，B、D在右室”，就是两个不同的微观态。当然“A在左室，B、C、D在右室”也是与前两个不同的微观态。

但是，宏观的观察并不能区分图10.5-1甲和乙的两个微观态，我们只能说两种情况下左右两室中分子的数密度是一样的，因此，我们说，图甲和图乙属于同一个宏观态；而图丙和图丁，尽管从微观上看具体分子的位置并不一样，是不同的微观态，它们也属于同一个宏观态，都是“左l右3”。

思考与讨论

对于A、B、C、D这4个分子来说，“左右各有2个分子”的微观状态有多少个？“左室有1个分子，右室有3个分子”的微观状态有多少个？

可以画简图把几种情况表示出来，然后进行统计。如果数学课中学过了“排列与组合”，计算会简单些。

撤去挡板后，从微观的角度来说，由于分子的热运动，图10.5-1所示的几种微观态，以及其他所有可能的微观态，它们各自出现的概率是一样的[1]。那么，宏观上观察到的现象是什么呢？

这4个分子在左右两室总共可能有16种不同的分布，即16种不同的微观态，如下表。

从表中看出，“左2右2”这种宏观上看来均匀分布的情况，所对应的微观态的个数最多，“左0右4”、“左4右0”这种极端不均匀的宏观态所对应的微观态的个数很少。

撤去挡板后，由于各个微观态出现的概率是一样的，从宏观上看，我们看到“左2右2”这种均匀分布的可能性最大，而分子重新集中在一个室中，另一个室变成真空的可能性最小。实际气体系统中的分子数大得惊人，两室中分子的数密度相同和大致相同的可能性比两室分子数相差很多的可能性大得多。因此，撤去挡板后实际上我们只能观察到气体向真空扩散，而不可能观察到气体分子重新聚集在一室的现象。

在这个例子中，“左2右2”这种状态对应着6个微观态，而一侧有4个分子另一侧为真空的状态只对应着2个微观态。按照我们前面的说法，“左2右2”是一种更为无序的状态。这与我们日常的感觉一致，即无序指一种“平均”“各处都一样”“没有差别”。

再通过摆积木的例子做些说明。一堆积木的木块杂乱地盛在箱子里，我们说它们是无序的，而按图摆成一个森林小屋，就说它是有序的。“盛在箱子里的积木”和“摆成小屋的积木”可以看做两个宏观状态，两者之中哪一个对应的微观状态比较多呢？按图摆成的森林小屋，虽然其中大小一样、颜色相同的木块也可以调换，但变化的余地很小，也就是说，对应于一定形状的小屋的微观态数目很少。但是对应于“盛在箱子里的积木”的微观态很多，因为无论你把哪个木块从上面移到下面，或把哪个木块的方向颠倒过来，它们都是“盛在箱子里的积木”这个宏观态的某个不同的微观态，我们看着都是乱糟糟的一箱。把一批积木随意倒在箱子中，这些木块的各种排列都可能发生，其中碰巧排成图中房子的可能性很小很小，而排成乱糟糟的可能性岂止千万种！所以，随意倾倒木块不可能出现房子！

这个例子再次表明，我们所说的有序状态，指的是对应着较少微观态的那样的宏观态。自发的过程总是倾向于出现与较多微观态对应的宏观态，因此自发的过程总是从有序向着无序发展的。

综合以上分析可以知道：一切自然过程总是沿着分子热运动的无序性增大的方向进行。这就是热力学第二定律的微观意义。

熵

通过前面的分析我们已经知道，系统的宏观状态所对应的微观态的多少表现为宏观态的无序程度，同时也决定了宏观过程的方向性。分析的结果归纳在以下表中。

看起来，一个宏观状态对应的微观状态的多少是个很重要的物理量，它标志着这个宏观态的无序程度，从中还可以推知系统将朝什么方向变化。物理学中用字母Ω表示一个宏观扶态所对应的微观状态的数目。

为了研究的方便，物理学家们用得更多的是一个与Ω相关的物理量，这就是今天常常听到的——熵（entropy），用字母S表示。玻耳兹曼在1877年提出了熵与微观态的数目Ω的关系，即S∝lnΩ，后来普朗克把它写成了等式

S＝klnΩ

式中k叫做玻耳兹曼常量。

如前所述，既然微观态的数目Ω是分子运动无序性的一种量度，由于Ω越大，熵S也越大，那么熵S自然也是系统内分子运动无序性的量度。

在引入熵之后，关于自然过程的方向性就可以表述为：在任何自然过程中，一个孤立系统的总熵不会减小。这就是用熵的概念表示的热力学第二定律。为此，不少人也把热力学第二定律叫做熵增加原理。

由熵的定义可知，熵较大的宏观状态就是无序程度较大的宏观状态，也就是出现概率较大的宏观状态。在自然过程中熵总是增加的，其原因并非因为有序是不可能的，而是因为通向无序的渠道要比通向有序的渠道多得多。把事情搞得乱糟糟的方式要比把事情做得整整齐齐的方式多得多。要让操场上的一群学生按班级、按身高，或按任何规则来站队都是比较麻烦的：每个学生都要寻找自己的位置。但是要让已经站好队的学生解散，那就非常简单：每个学生随便朝一个方向跑去，队形就乱了。

从微观的角度看，热力学第二定律是一个统计规律：一个孤立系统总是从熵小的状态向熵大的状态发展，而熵值较大代表着较为无序，所以自发的宏观过程总是向无序度更大的方向发展。

做一做

目前“熵”这个词的应用十分广泛，已经超出了物理学的范畴，深入到信息科学、生命科学和社会科学中。在这些场合中，有些用法是熵的本来意义的延伸，有些只是用做“无序程度”的代名词，描述过程的发展方向。

登录一个有搜索功能的网站，键入“熵”宇，看看人们是怎样应用这个名词的。

科学漫步

向绝对零度逼近

在冷热王国里，人们在两个方向上进行着执著的探索。一方面，人们向高温进军，希望能制造和控制越来越高的温度，去实现受控热核反应和模拟宇宙诞生初期的情景；在另一个方向上，人们努力向绝对零度逼近，希望揭示低温世界的秘密。

什么是绝对零度？我们在初中学过，宇宙中存在着温度的下限：-273.15℃。热力学温度是以这个下限为起点的，用T表示。而- 273.15℃也就叫做热力学零度或绝对零度，即T=0 K。

我们现在已经知道的一些低温值如下表所示。

从表中可以看出，实验室中的低温已经非常接近热力学零度了。随着科学技术的发展，还有希望获得更低的温度。

在低温领域里，物质呈现出超导、超流等许多新奇的特性，为新材料研制、磁悬浮、直流输电以及生物技术等高科技拓展了广阔的发展空间。然而，人们发现温度越低，降温越困难。在德国科学家W．H．能斯脱等人的工作基础上，人们在20世纪初总结出了一条新的规律：不可能通过有限的过程把一个物体冷却到绝对零度。这个规律称做热力学第三定律（third law of thermodynamics）。

尽管热力学零度不可能达到，但是温度总有可能降低。因此，热力学第三定律不阻止人们想办法尽可能地接近绝对零度。

问题与练习

1．一个封闭的方盒内有两个隔板，把方盒隔成了三个小房间，每个小房间内有2个球，球上各有一个字，小房间内球上的字恰好组成图10.5-2所示的三个词（从左向右念）。摇动方盒，球在小房间内的左右位置可以变换。

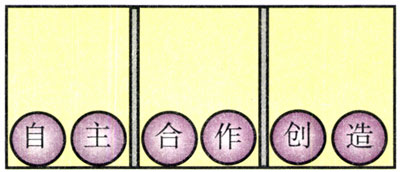
（1）图中6个球同时排列成这三个词的概率是多少？

（2）取去其中一个隔板，摇动方盒，6个球能同时排列成这三个词的概率又是多少？

（3）把两个隔板全部取去，摇动方盒，6个球能同时排列成这三个词的概率又是多少？

（4）在这个封闭的方盒内，取消隔板让小球充分地运动，其无序性是增大了还是减小了？

2．成语“覆水难收”指的是一盆水泼出后是不可能再回到盆中的。请从不同宏观态所对应的微观态数目不同这个角度，解释为什么水不会自发地聚到盆中。

发布时间：2017/6/6 上午8:31:52  阅读次数：1035