第八章 4 气体热现象的微观意义

从微观的角度看，物体的热现象是由大量分子的热运动所决定的。尽管个别分子的运动有它的不确定性，但大量分子的运动情况会遵从一定的统计规律，生活中的事例也有类似的特点。

实验

每人都把4枚硬币握在手中，在桌面上随意投掷10次，记录每次投掷时正面朝上的硬币个数，统计总共10次投掷中有0，1，2，3，4枚硬币正面朝上的次数各是多少，把结果填在以下表格的第1行。

以3～4人为一个小组，把小组中各人统计的数字累计起来，填在表格中第2行。

按座位把全班分成几个大组，把每个大组中各小组统计的数字累计起来，填在表格中第3行。

把各大组的数字累计起来，得到全班的统计数字，填在表格第4行。

随着投掷次数的增多，2枚硬币正面朝上的次数比例最多，约占总数的\(\frac{3}{8}\)；1枚和3枚硬币朝上的次数比例略少，分别约占总数的\(\frac{1}{4}\)，全部朝上和全部朝下的次数最少，各约占总数的\(\frac{1}{16}\)。投掷中，不同枚数硬币同时正面朝上的出现次数如图8.4-1所示。它表明，个别事物的出现具有偶然的因素，但大量事物出现的机会，却遵从一定的统计规律。

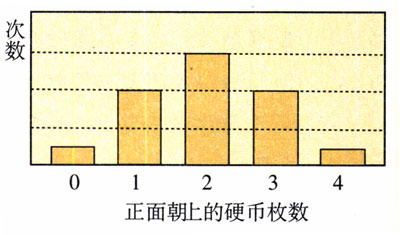
说一说

上面的实验中，如果在每枚硬币的背面都贴上与它直径相同的铬片，实验结果可能会有什么不同？

社会中的统计规律随处可见。例如，在保险公司投保“人身意外伤害险”时，要按不同的职业交纳不同的保险费；又如，通过人口健康普查的统计数据，可以发现某些地区存在着高发病率的疾病。尽管事先不能知道究竟哪个人以后会患这种疾病，但这个地区很可能存在该病的诱因，我们要对这个地区人群的生活习惯和环境等做进一步调查，以发现这个诱因。

气体分子运动的特点

热现象与大量分子热运动的统计规律有关。要研究气体的热现象，就要了解气体分子运动的特点。

可以认为液体的分子是一个挨着一个地排列的。液体变为气体，体积要增大上千倍，可见气体分子间的距离大约是分子直径的10倍左右，分子的大小相对分子间的空隙来说很小，所以能够把分子视为质点。由于气体分子间的距离比较大，分子间的作用力很弱，通常认为，气体分子除了相互碰撞或者跟器壁碰撞外，不受力而做匀速直线运动，因而气体能充满它能达到的整个空间。

虽然气体分子的分布比液体稀疏，但分子的数密度[1]仍然十分巨大，标准状态下1 cm³气体中的分子数比地球上的人口总数还要多上许多亿倍。因此，分子之间频繁地发生碰撞，使每个分子的速度大小和方向频繁地改变。分子的运动杂乱无章，在某一时刻，向着任何一个方问运动的分子都有，而且向各个方向运动的气体分子数目都相等。当然，这里说的数目相等，是针对大量分子说的，实际数目会有微小的差别，由于分子数极多，其差别完全可以忽略。

尽管大量分子做无规则运动，速率有大有小，但分子的速率却按一定的规律分布。表8.4-1是氧气分子在0℃和100℃两种不同情况下的速率分布情况。图8.4-2是根据表格中的数据绘制的图象。

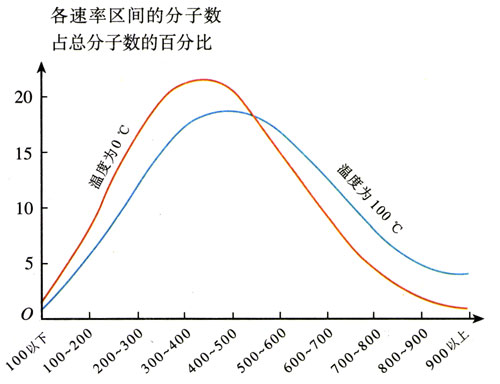
可以看到，0℃和100℃氧气分子的速率都呈“中间多、两头少”的分布，但这两个温度下具有最大比例的速率区间是不同的，0℃时300～400 m/s速率的分子最多，100℃时400～500 m/s速率的分子最多。100℃的氧气，速率大的分子比例较多，其分子的平均速率比0℃的大。从这里我们可以直观地体会“温度越高，分子的热运动越激烈”这句话的含义。

定量的分析可以得出：理想气体的热力学温度T与分子的平均动能\({\bar E_k}\) 成正比，即

T＝a\({\bar E_k}\)

式中a是比例常数。

这表明温度是分子平均动能的标志。

气体压强的微观意义

从微观的角度看，气体对容器的压强是大量气体分子对容器的碰撞引起的，这就好像密集的雨点打在伞上一样，雨点虽然是一滴一滴地打在伞上，大量密集雨点的撞击，使伞受到持续的作用力。

演示

用豆粒做气体分子的模型，可以演示气体压强产生的机理。

把一颗豆粒拿到台秤上方约10 cm的位置，放手后使它落在秤盘上，观察秤的指针的摆动情况。

再从相同高度把100粒或者更多的豆粒连续地倒在秤盘上（图8.4-4），观察指针的摆动情况。

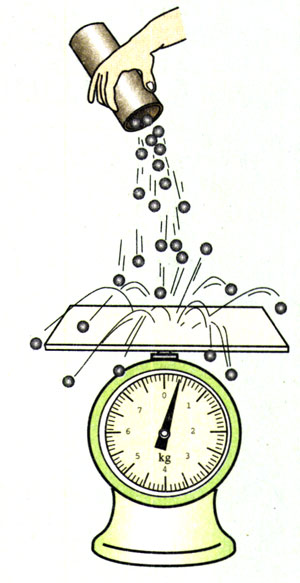
使这些豆粒从更高的位置落在秤盘上，观察指针的摆动情况。

从微观角度来看，气体压强的大小跟两个因素有关：一个是气体分子的平均动能，一个是分子的密集程度。

对气体实验定律的微观解释

用分子动理论可以很好地解释气体的实验定律。

一定质量的某种理想气体，温度保持不变时，分子的平均动能是一定的。在这种情况下，体积减小时，分子的密集程度增大，气体的压强就增大。这就是玻意耳定律的微观解释。

一定质量的某种理想气体，体积保持不变时，分子的密集程度保持不变。在这种情况下，温度升高时，分子的平均动能增大，气体的压强就增大。这就是查里定律的微观解释。

一定质量的某种理想气体，温度升高时，分子的平均动能增大。只有气体的体积同时增大，使分子的密集程度减小，才能保持压强不变。这就是盖-吕萨克定律的微观解释。

科学漫步

星体表面的大气蒸发

由于气体分子在不断地高速运动，地球的大气中不断有气体分子像人造卫星一样飞向星际空间，这种现象称为大气蒸发。

在力学中我们已经知道，行星表面上物体的逃逸速度可以表示为

v_s＝\(\sqrt {2gR} \)

式中R和g分别为行星的半径和行星表面附近的自由落体加速度。下表列出了太阳系中几个行星的逃逸速度v_s。

实际上，气体分子要从星球表面逃逸出去，除了速率必须大于v_s外，还要保证它在飞行中不会与其他分子相撞。

由于越高的位置大气越稀薄，所以对每个行星都存在一个高度，超过这个高度后就可以不考虑分子间的碰撞了。这个高度称为逃逸高度。

对地球而言，逃逸高度约为500 km，这里的温度接近600K。利用温度与分子平均动能的关系，可以算出不同气体分子的平均速率。例如，600 K时氢气分子和氧气分子的平均速率分别为2.58 km/s和0.67 km/s，它们与地球上的v_s的比值分别为\(\frac{1}{4.34}\)和\(\frac{1}{16.7}\)。虽然氢气分子和氧气分子的平均速率都比v_s小得多，但我们知道，总有一些分子的速率比平均速率大，有的甚至大很多，所以大气中总包含速率大于v_s的分子，它们可以逃出地球。

根据分子速率的分布规律，如果大气中某种分子的平均速率是逃逸速率v_s的\(\frac{1}{3.5}\)，这种气体将于5万年内消失；如上述比值为\(\frac{1}{4}\)，则这种气体要经过3千万年才能消失；如果比值为\(\frac{1}{4.4}\)，则要经过250亿年才会消失。地球的年龄约为45亿年，由于大气中氢气分子的平均速率较大，因此地球大气中氢的含量很少。

不同星体上的气体都遵从气体分子速率的分布规律，所以由星体上v_s的数值和行星表面的温度就可以确定：在太阳系里除地球以外，能有大气的行星是金星、土星、木星、天王星和海王星。火星只能保存一些大气的残余，主要由密度较大的气体（如二氧化碳、氩）组成。这些都已为行星光谱的观测所证实。

问题与练习

1．请列举一个日常生活中表现统计规律的事例。

2．一定质量的某种理想气体，当它的热力学温度升高为原来的1.5倍、体积增大为原来的3倍时，压强将变为原来的多少？请你从压强和温度的微观意义来说明。

发布时间：2017/5/23 上午7:51:29  阅读次数：2212