第八章 3 理想气体的状态方程

理想气体

玻意耳定律、查理定律、盖-吕萨克定律等气体实验定律，都是在压强不太大（相对大气压强）、温度不太低（相对室温）的条件下总结出来的。当压强很大、温度很低时，上述定律的计算结果与实际测量结果有很大的差别。例如：有一定质量的氦气，压强与大气压相等，体积为1 m³，温度为0℃。在温度不变的条件下，如果压强增大到大气压的500倍，按玻意耳定律计算，体积应该缩小至\(\frac{1}{500}\)m³，但是实验结果是\(\frac{1.36}{500}\)m³。如果压强增大到大气压的1 000倍，体积实际减小至\(\frac{2.07}{1000}\)m³，而不是按玻意耳定律计算得到的\(\frac{1}{1000}\)m³。

尽管如此，很多实际气体，特别是那些不容易液化的气体，如氢气、氧气、氮气、氦气等，在通常温度和压强下，其性质与实验定律的结论符合得很好。为了研究方便，可以设想一种气体，在任何温度、任何压强下都遵从气体实验定律，我们把这样的气体叫做理想气体（ideal gas）。在温度不低于零下几十摄氏度、压强不超过大气压的几倍时，把实际气体当成理想气体来处理，误差很小，可是计算起来却简便多了。

理想气体的状态方程

描述一定质量的某种理想气体状态的参量有三个：p、V、T。前面提到的每一个实验定律所谈的，都是当一个参量不变时另外两个参量的关系。这节我们将研究三个参量都可能变化的情况下，它们所遵从的数学关系式。

思考与讨论

如图8.3-1，一定质量的某种理想气体从A到B经历了一个等温过程，从B到C经历了一个等容过程。分别用p_A、V_A、T_A和p_B、V_B、T_B以及p_C、V_C、T_C表示气体在A、B、C三个状态的状态参量，请同学们尝试导出状态A的三个参量p_A、V_A、T_A和状态C的三个参量p_C、V_C、T_C之间的关系。

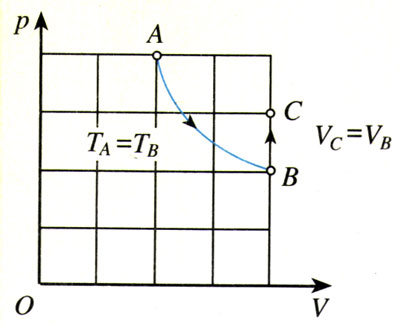
推导过程中要注意：

1．先要根据玻意耳定律和查理定律分别写出p_A、V_A与p_B、V_B的关系及p_B、T_B与p_C、T_C的关系；

2．由于要推导A、C两个状态之间的参量的关系，所以最后的式子中不能出现状态B的参量。为此，要在写出的两式中消去p_B，同时还要以T_A代替T_B（因为A→B是等温过程，两个状态的温度是相等的）、以V_C代替V_B（因为B→C是等容过程，两个状态的体积是相等的）。

在图8.3-1所示的两个过程中，把A→B的玻意耳定律方程和B→C的查理定律方程联立，消去两个方程中状态B的压强，便得到关系式

\(\frac{{{p_{\rm{A}}}{V_{\rm{A}}}}}{{{T_{\rm{A}}}}}\)＝\(\frac{{{p_{\rm{C}}}{V_{\rm{C}}}}}{{{T_{\rm{C}}}}}\)

这里A、C是气体的两个任意状态。上面的式子表明，一定质量的某种理想气体，在从状态1变化到状态2时，尽管其p、V、T都可能改变，但是压强跟体积的乘积与热力学温度的比值保持不变。也就是说

\(\frac{{{p_1}{V_1}}}{{{T_1}}}\)＝\(\frac{{{p_2}{V_2}}}{{{T_2}}}\)                       （1）

或

\(\frac{{pV}}{T}\)＝C                               （2）

式中C是与p、V、T无关的常量。

上面两式都叫做一定质量的某种理想气体的状态方程（state equation of ideal gas）。

【例题】一定质量的某种理想气体由状态A变为状态D，其有关数据如图8.3-2所示。若状态D的压强是10⁴ Pa，状态A的压强是多少？

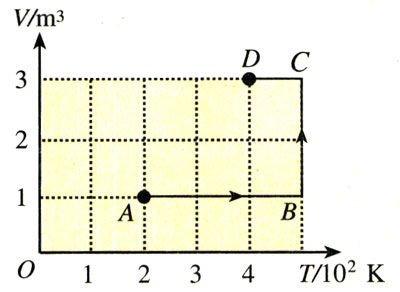
【解】从题目所给的条件可以看出，A、D两个状态中共有5个状态参量是已知的

V_A=1 m³，T_A=200 K，

V_D=3 m³，T_D=400 K，p_D=10⁴ Pa

待求的状态参量是p_A。

根据题意，研究的对象是一种理想气体，而且质量是一定的。由理想气体状态方程把这些状态参量联系起来，即

\(\frac{{{p_{\rm{A}}}{V_{\rm{A}}}}}{{{T_{\rm{A}}}}}\)＝\(\frac{{{p_{\rm{D}}}{V_{\rm{D}}}}}{{{T_{\rm{D}}}}}\)

由此解出

p_A＝\(\frac{{{p_{\rm{D}}}{V_{\rm{D}}}{T_{\rm{A}}}}}{{{V_{\rm{A}}}{T_{\rm{D}}}}}\)

代入数值后得到状态A的压强

p_A＝\(\frac{{{{10}^4} \times 3 \times 200}}{{1 \times 400}}\) Pa＝1.5×10⁴ Pa

从这个例题可以看出，一定质量的理想气体的状态方程给出了两个状态间的联系，并不涉及气体从一个状态变到另一个状态的具体方式。

问题与练习

1．对一定质量的气体来说，能否做到以下各点？

（1）保持压强和体积不变而改变它的温度。

（2）保持压强不变，同时升高温度并减小体积。

（3）保持温度不变，同时增加体积并减小压强。

（4）保持体积不变，同时增加压强并降低温度。

2．某柴油机的气缸容积为0.83×10^-3 m³，压缩前其中空气的温度为47℃、压强为0.8×10⁵ Pa。在压缩冲程中，活塞把空气压缩到原体积的\(\frac{1}{17}\)，压强增大到40×10⁵ Pa，求这时空气的温度。

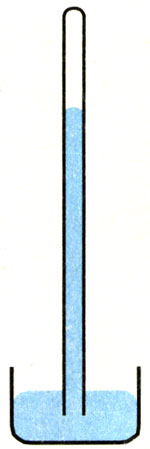
3．在做托里拆利实验时，玻璃管内有些残存的空气，此时玻璃管竖直放置，如图8.3-3。假如把玻璃管竖直向上提起一段距离，玻璃管下端仍浸在水银中，则管内空气体积如何变化？管内水银柱长度如何变化？管内空气压强如何变化？

发布时间：2017/5/22 下午2:14:22  阅读次数：1744