第八章 1 气体的等温变化

要推论宏观物质的表现，就必须采用统计方法，由对个体原子（分子）物理参量的适当统计平均，来得出支配宏观行为的规律。

——罗杰·彭罗斯[1]

燃烧器喷出熊熊烈焰，巨大的气球缓缓膨胀……这个场景是否让你想起儒勒·凡尔纳[2]的小说《气球上的五星期》？书中描述了一位充满冒险精神的旅行家，他乘坐自己设计的热气球，经历无数艰难险阻，对非洲进行了考察。

热气球在那时还只是用于探险，但现在已经在为人们的休闲娱乐服务。如果有朝一日你乘坐热气球在蓝天翱翔，或许你还能回想起它的工作原理。

第八章 1 气体的等温变化

打足气的自行车在烈日下曝晒，常常会爆胎，原因是车胎内的气体因温度升高而压强增大、体积膨胀。生活中的许多现象都表明，气体的压强、体积、温度三个状态参量之间存在着一定的关系。本节我们研究一种特殊情况：一定质量的气体，在温度不变的条件下其压强与体积变化时的关系。我们把这种变化叫做等温变化。

实验

研究气体等温变化的规律

如图8.1-1，注射器下端的开口有橡胶塞，它和柱塞一起把一段空气柱封闭在玻璃管中。这段空气柱是我们研究的对象，实验过程中它的质量不会变化；实验中如果空气柱体积的变化不太快，它的温度大致等于环境温度，也不会有明显的变化。

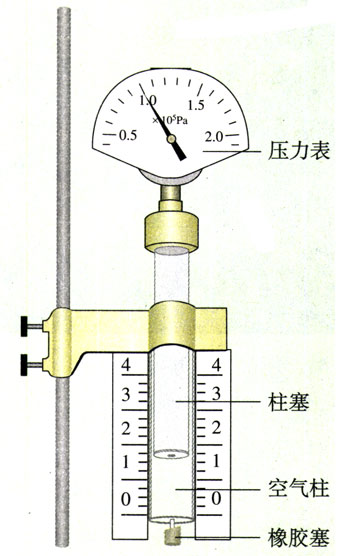
1．实验数据的收集

空气柱的压强p可以从仪器上方的指针读出，空气柱的长度，可以在玻璃管侧的刻度尺上读出，空气柱的长度l与横截面积S的乘积就是它的体积V。

用手把柱塞向下压或向上拉，读出体积与压强的几组数据。

2．实验数据的处理

很容易发现，空气柱的体积越小，压强就越大。空气柱的压强是否跟体积成反比呢？我们可以通过图象来检验这个猜想。

以压强p为纵坐标，以体积的倒数\(\frac{1}{V}\)为横坐标，把以上各组数据在坐标系中描点。如果图象中的各点位于过原点的同一条直线上，就说明压强跟体积的倒数成正比，即压强的确与体积成反比。如果不在同一条直线上，我们再尝试其他关系。

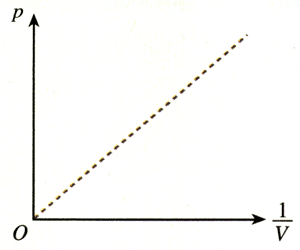
如果把实验数据输入计算机，借用数表软件可以在短时间内进行多种尝试，很快获得对应的图象，得知p与V的关系。

3．要考虑的问题

在这个实验中，为了找到体积与压强的关系，是否一定要测量空气柱的横截面积？

用刻度尺检查可以发现，玻璃管侧的刻度尽管是均匀的，但并非准确地等于1 cm、2 cm……这对实验结果的可靠性是否有影响？

测量体积时误差主要出在哪里？怎样减小这个误差？

玻意耳定律

英国科学家玻意耳（R．Boyle，1627～1691）和法国科学家马略特（E．Mariotte，1620～1684）各自通过实验发现，一定质量的某种气体，在温度不变的情况下，压强p与体积V成反比，即p∝\(\frac{1}{V}\)。写成公式就是

pV＝C                         （1）

式中C是一个常量。或者

p₁V₁＝p₂V₂                   （2）

其中p₁、V₁和p₂、V₂分别表示气体在1、2两个不同状态下的压强和体积。

这个规律叫做玻意耳定律（Boyle law）。

气体等温变化的p-V图象

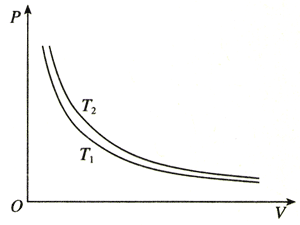
我们在探究一定质量气体压强跟体积关系的实验中，为了用线性关系来检验这两个物理量之间的定量规律，建立了图8.1-2中p-\(\frac{1}{V}\)的坐标系。然而，为了直观地描述压强p跟体积V的关系，通常还是用p-V坐标系。一定质量气体等温变化的p-V图象如图8.1-3所示，图线的形状为双曲线。由于它描述的是温度不变时的p-V关系，因此称它为等温线。一定质量的气体，不同温度下的等温线是不同的，如图8.1-3。

思考与讨论

图8.1-3中有两条等温线，你能判断哪条等温线表示的是温度比较高时的情形吗？

你是根据什么理由做出判断的？

问题与练习

1．一个足球的容积是2.5 L。用打气筒给这个足球打气，每打一次都把体积为125 mL、压强与大气压相同的气体打进球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同，打了20次后，足球内部空气的压强是大气压的多少倍？你在得出结论时考虑到了什么前提？实际打气时的情况能够满足你的前提吗？

2．水银气压计中混入了一个气泡，上升到水银柱的上方，使水银柱上方不再是真空。当实际大气压相当于768 mm高的水银柱产生的压强时，这个水银气压计的读数只有750 mm，此时管中的水银面到管顶的距离为80 mm。当这个气压计的读数为740 mm水银柱时，实际的大气压是多少？设温度保持不变。

3．在验证玻意耳定律的实验中，实验小组记录了一系列数据。但是，仅就以下表格中的两组数据来看，小王和小李却有完全不同的看法：小王认为，这两组数据很好地体现了玻意耳定律的规律，因为两组数据p和V的乘积几乎相等，说明p跟V成反比；小李却认为，如果把这两组数据在纵坐标轴为p、横坐标轴为\(\frac{1}{V}\)的坐标系中描点，这两点连线的延长线将不经过坐标原点，因此这两组数据没有反映玻意耳定律的规律。对此你有什么看法？

发布时间：2017/5/17 下午3:29:09  阅读次数：2028