第七章 3 分子间的作用力

演示

取一枝长约1 m的玻璃管，注入半管清水，再注入酒精，使液面几乎达到管口。上下几次颠倒玻璃管，观察管中液体体积的变化。

这个实验说明了什么？

分子间的作用力

气体很容易被压缩，说明气体分子之间存在着很大的空隙。水和酒精混合后总体积会减小，说明液体分子之间存在着空隙。压在一起的金片和铅片，各自的分子能扩散到对方的内部，说明固体分子之间也存在着空隙。

分子间虽然有空隙，大量分子却能聚集在一起形成固体或液体，说明分子之间存在着引力。用力拉伸物体，物体内要产生反抗拉伸的弹力，说明分子间存在着引力。把两块纯净的铅压紧，它们会“粘”在一起，甚至下面吊一个重物也不能把它们拉开，这也说明分子间存在引力。

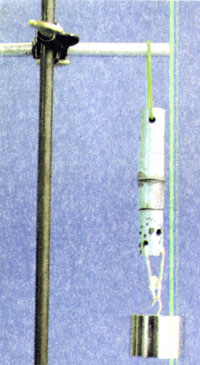
分子间有空隙，但是用力压缩物体，物体内会产生反抗压缩的弹力，这说明分子之间还存在着斥力。

深入的研究表明，两个邻近的分子之间的确同时存在着引力和斥力，引力和斥力的大小都跟分子间的距离有关，它们随分子间距离变化的关系如图7.3-2所示。图中的横坐标r表示两个分子间的距离，纵坐标F_斥和F_引的绝对值分别表示其中一个分子所受斥力和引力的大小。图中上面的曲线表示F_斥随r变化的关系，下面的曲线表示F_引随r变化的关系。

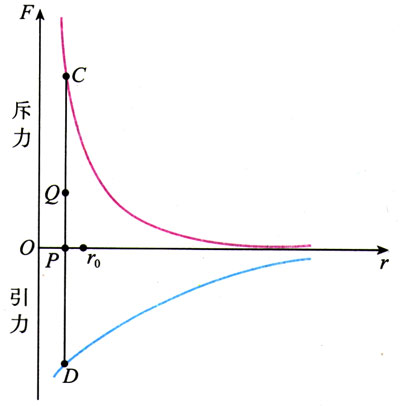
从图7.3-2可以看到，F_斥和F_引都随着r的增大而减小，但F_斥比F_引减小得更快。当两个分子的距离为r₀时，其中一个分子所受的引力与斥力相等，那么这个分子所受的合力为0。当分子间的距离小于r₀时，作用力的合力表现为斥力；当分子间的距离大于r₀时，作用力的合力表现为引力。

思考与讨论

请在图7.3-2中作出一个分子所受另一个分子的斥力与引力的合力随分子间距离r变化的图象。例如，当r＝OP时，这个分子所受斥力的大小可以用线段PC的长度表示，所受引力的大小用PD的长度表示。从C向下作CQ＝PD，于是线段PQ的长度就代表了合力F的大小：F＝F_斥－F_引。

再作出r取其他大约10个值时代表合力的点，连成平滑曲线。这条曲线将在本章第5节用到，因此作图时要尽可能准确。

讨论这条曲线的含义。

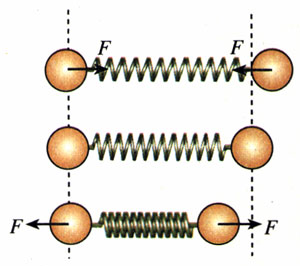
分子间作用力的合力有些像弹簧连接着的两个小球间的作用力：拉伸时表现为引力，压缩时表现为斥力。

分子动理论

通过前面的学习我们已经知道：物体是由大量分子组成的，分子在做永不停息的无规则运动，分子之间存在着引力和斥力。这就是分子动理论（molecular kinetic theory）的主要内容。

本册课本的中心是热学。热学包括两个方面：一方面是关于热现象的宏观理论，它研究热现象的一般规律，不涉及热现象的微观解释；另一方面是关于热现象的微观理论，从分子运动的角度来研究宏观热现象的规律。分子动理论就是热现象微观理论的基础。

由于物体是由数量极多的分子组成的，这些分子并没有统一的运动步调，单独来看，各个分子的运动都是不规则的、带有偶然性的，但从总体来看，大量分子的运动却有一定的规律，这种规律叫做统计规律（statistical regularity）。大量分子的集体行为受到统计规律的支配。

问题与练习

1．请描述：当两个分子间的距离由小于r₀逐渐增大，直至远大于r₀时，分子间的引力如何变化？分子间的斥力如何变化？分子间引力与斥力的合力又如何变化？

2．当两个分子间的距离由图7.3-2中的r₀逐渐增大时，分子间相互作用力的合力会出现一个极大值。你能否用实际生活中的例子说明分子间相互作用的合力的确存在着这样的极大值？

3．为什么物体能够被压缩，但压缩得越小，进一步压缩就越困难？

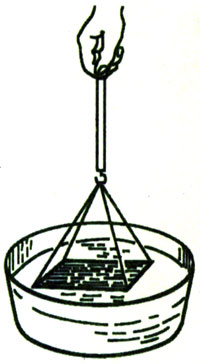
4．如图7.3-4，把一块洗净的玻璃板吊在橡皮筋的下端，使玻璃板水平地接触水面。如果你想使玻璃板离开水面，必须用此玻璃板重量大的力向上拉橡皮筋。动手做一做，并解释为什么。

发布时间：2017/5/12 上午11:16:43  阅读次数：2590