第三章 6 带电粒子在匀强磁场中的运动

图3.6-1是洛伦兹力演示仪。电子束由电子枪产生，玻璃泡内充有稀薄的气体，在电子束通过时能够显示电子的径迹。励磁线圈的原理与图3.3-8相同，它能够在两线圈之间产生匀强磁场，磁场的方向与两线圈中心的连线平行。电子的速度大小和磁感应强度可以分别通过电子枪的加速电压和励磁线圈的电流来调节。

演示

用洛伦兹力演示仪观察运动电子在磁场中的偏转。在做以下每项观察之前，首先进行讨论，根据洛伦兹力的知识预测电子束的径迹，然后观察，检验你的预测。

1．不加磁场时观察电子柬的径迹。

2．给励磁线圈通电，在玻璃泡中产生沿两线圈中心连线方向、由纸内指向读者的磁场，观察电子束的径迹。

3．保持出射电子的速度不变，改变磁感应强度，观察电子束径迹的变化。

4．保持磁感应强度不变，改变出射电子的速度，观察电子束径迹的变化。

带电粒子在匀强磁场中的运动

带电粒子在磁场中运动时，它所受的洛伦兹力总与速度方向垂直，洛伦兹力在速度方向没有分量，所以洛伦兹力不改变带电粒子速度的大小，或者说，洛伦兹力不对带电粒子做功，不改变粒子的能量。

由于粒子速度的大小不变，所以粒子在匀强磁场中所受洛伦兹力的大小也不改变，加之洛伦兹力总与速度方向垂直，正好起到了向心力的作用。所以，沿着与磁场垂直的方向射入磁场的带电粒子，在匀强磁场中做匀速圆周运动。

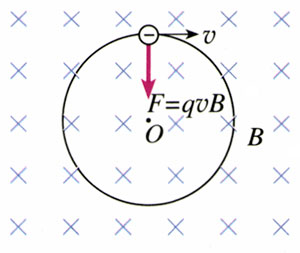
思考与讨论

带电粒子在匀强磁场中做匀速圆周运动的圆半径，与粒子的速度、磁场的磁感应强度有什么关系？

考虑到粒子所受的洛伦兹力就是它做匀速圆周运动的向心力，列出方程来不难解出几个物理量的关系式。然后就可以分别判断粒子的速度、磁场的强弱对圆半径的影响。

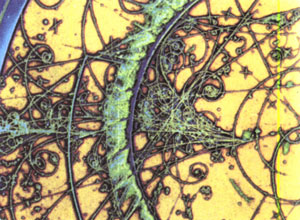
在粒子物理的研究中，可以让粒子通过“云室”“汽泡室”等装置，显示它们的径迹。如果在云室、汽泡室中施加匀强磁场，可以看到带电粒子运动的圆形径迹。粒子的质量、速度、带电多少不一样，径迹的半径也不一样。

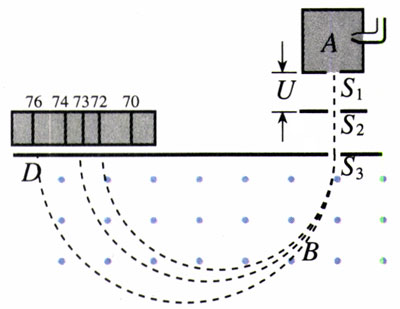
【例题】一个质量为m、电荷量为q的粒子，从容器下方的小孔S₁飘入电势差为U的加速电场，其初速度几乎为零，然后经过S₃沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中，最后打到照相底片D上（图3.6-4）。

（1）求粒子进入磁场时的速率。

（2）求粒子在磁场中运动的轨道半径。

【解】（1）粒子进入磁场时的速度v等于它在电场中被加速而得到的速度。由动能定理，粒子得到的动能\(\frac{1}{2}\)mv²等于它在S₁、S₂之间的加速电场中运动时电场对它做的功qU，即

\(\frac{1}{2}\)mv²＝qU

由此解得

v＝\(\sqrt {\frac{{2qU}}{m}} \)

（2）粒子在磁场中只受洛伦兹力的作用，这个力与运动方向垂直，不能改变粒子运动的速率，所以粒子的速率总是v，做匀速圆周运动。设圆半径为r，粒子做匀速圆周运动的向心力可以写为\(\frac{{m{v^2}}}{r}\)，而洛伦兹力为qvB，二者相等，即

qvB＝\(\frac{{m{v^2}}}{r}\)

由此解出

r＝\(\frac{{mv}}{{qB}}\)

把第（1）问中求得的v代入，得出粒子在磁场中做匀速圆周运动的轨道半径

r＝\(\frac{1}{B}\sqrt {\frac{{2mU}}{q}} \)

从这个结果可以看出，如果容器A中粒子的电荷量相同而质量不同，它们进入磁场后将沿着不同的半径做圆周运动，因而打到照相底片的不同地方，如图3.6-4中的D。这样的仪器叫做质谱仪。从粒子打在底片上的位置可以测出圆周的半径r，进而可以算出粒子的比荷\(\frac{q}{m}\)或算出它的质量。

质谱仪最初是由汤姆生的学生阿斯顿设计的，他用质谱仪发现了氖20和氖22，证实了同位素的存在。现在质谱仪已经是一种十分精密的仪器，是测量带电粒子的质量和分析同位素的重要工具。

回旋加速器

要认识原子核内部的情况，必须把核“打开”进行“观察”。然而，原子核被强大的核力约束，只有用极高能量的粒子作为“炮弹”去轰击，才能把它“打开”。产生这些高能“炮弹”的“工厂”就是各种各样的粒子加速器。

由于电场力可以对带电粒子做功，从而增加粒子的能量，因此，人们首先想到加速器中一定要用到电场。加速电压越高，粒子获得的能量就越高。然而产生过高的电压在技术上是很困难的。于是人们进一步设想，能不能采用多次（多级）加速的方法呢？

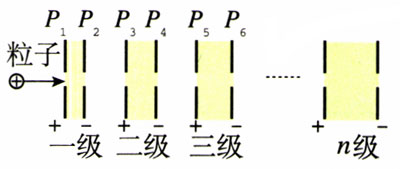
在图3.6-5所示的多级加速器中，由于粒子在加速过程中的径迹为直线，其加速装置要很长很长。人们进一步思考，如果带电粒子在一次加速后又转回来被第二次加速，如此往复“转圈圈”式地被加速，加速器装置所占的空间不是会大大缩小吗？而磁场正好能使带电粒子“转圈圈”！于是，人们依据这个思路设计出了用磁场控制轨道、用电场进行加速的回旋加速器（cyclotron）。

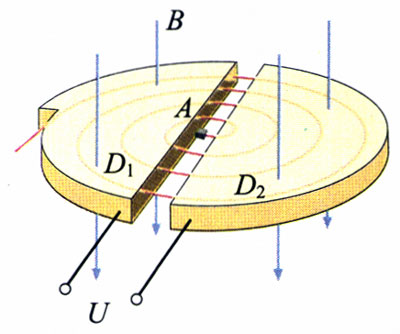
回旋加速器的工作原理如图3.6-6所示。D₁和D₂是两个中空的半圆金属盒，它们之间有一定的电势差U。A处的粒子源产生的带电粒子，在两盒之间被电场加速。两个半圆盒处于与盒面垂直的匀强磁场B中，所以粒子在磁场中做匀速圆周运动。经过半个圆周之后，当它再次到达两盒间的缝隙时，控制两盒间的电势差，使其恰好改变正负，于是粒子经过盒缝时再一次被加速。如此，粒子在做圆周运动的过程中一次一次地经过盒缝，而两盒间的电势差一次一次地反向，粒子的速度就能够增加到很大。

思考与讨论

假如粒子每两次经过盒缝的时间间隔[1]相同，控制两盒间电势差的正负变换是比较容易的。但是粒子的运动越来越快，也许粒子走过半圆的时间间膈越来越短，这样两盒间电势差的正负变换就要越来越快，从而造成技术上的一个难题。实际情况是这样吗？

图3.6-6中，粒子每经过一次加速，它的轨道半径就大一些，这样画对吗？

利用带电粒子在匀强磁场中运动的知识，分别计算粒子运动的周期（绕圆运动一周的时间）与速度的关系和半径与速度的关系，就能回答这两个问题。

回旋加速器加速的带电粒子，能量达到25～30 MeV后，就很难再加速了。原因是，按照狭义相对论，粒子的质量随着速度的增加而增大，而质量的变化会导致其回转周期的变化，从而破坏了与电场变化周期的同步。关于质量与速度的关系，我们将在选修3-4中学到。

问题与练习

1．电子以1.6×10⁶ m/s的速度沿着与磁场垂直的方向射入B＝2.0×10^-4 T的匀强磁场中。求电子做匀速圆周运动的轨道半径和周期。

2．已知氚核的质量约为质子的3倍，带正电荷，电荷量为一个元电荷；α粒子即氦原子核，质量约为质子的4倍，带正电荷，电荷量为元电荷的2倍。现在质子、氚核和α粒子在同一匀强磁场中做匀速圆周运动。求以下情况下它们运动半径之比：

（1）它们的速度大小相等；

（2）它们由静止经过相同的加速电场加速后进入磁场。

3．A、B是两种同位素的原子核，它们具有相同的电荷、不同的质量。为测定它们的质量比，使它们从质谱仪的同一加速电场由静止开始加速，然后沿着与磁场垂直的方向进入同一匀强磁场，打到照相底片上。如果从底片上获知A，B在磁场中运动轨迹的直径之比是1.08∶1，求A、B的质量之比。

3．回旋加速器D形盒的半径为r，匀强磁场的磁感应强度为B。一个质量为m、电荷量为q的粒子在加速器的中央从速度为零开始加速。根据回旋加速器的这些数据，请估算该粒子离开回旋加速器时获得的动能。

发布时间：2017/5/5 上午8:15:58  阅读次数：2276