第二章 6 电阻定律

影响导体电阻的因素

我们已经知道，导体的电阻是导体本身的一种性质，由导体自身的因素决定，那么，它到底由哪些因素决定呢？移动滑动变阻器的滑片可以改变它的电阻，这说明导体电阻跟它的长度有关；同是220 V的灯泡，灯丝越粗用起来越亮，说明导体电阻跟横截面积有关；电线常用铜丝制造而不用铁丝，说明导体电阻跟它的材料有关。

本节就来探究导体的电阻与以上这些因素的定量关系。实验时可以在铁丝、康铜丝、电炉丝（镍铬合金丝）等不同金属丝中选择几种，测量它们的横截面积、长度、电阻，从中找出关系。关于这些物理量的测量方法，建议如下。

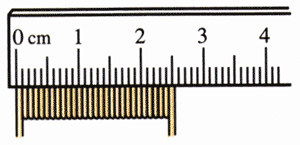
取一段新的紧密绕制的电炉丝，如图2.6-1那样用刻度尺测出它的宽度，除以圈数，便是电炉丝的直径，于是可以算出电炉丝的横截面积S。测量铜丝的横截面积时，可以使用类似的方法[1]。

把电炉丝拉直，或者用一根已经被拉直的同一规格的电炉丝，用刻度尺量出它的长度l。

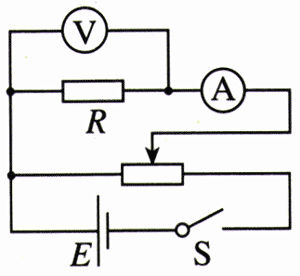
可以用图2.6-2的电路测量电炉丝的电阻R：闭合开关后，测出电炉丝两端的电压、通过电炉丝的电流，然后根据欧姆定律算出电炉丝的电阻。改变滑动变阻器滑片的位置，能获得多组数据，以各组电阻数据的平均值为R。

通过测量得到所霈数据后，怎样得出结论？以下方案可供参考。

探究方案一

我们可以通过实验在长度、横截面积、材料三个因素中，保持两个因素不变，比较第三个因素的影响；然后研究另外两个因素的影响。

实验

探究导体电阻与其影响因素的定量关系

如图2.6-3，a、b、c、d是四条不同的金属导体。在长度、横截面积、材料三个因素方面，b、c、d跟a相比，分别只有一个因素不同：b与a长度不同；c与a横截面积不同；d与a材料不同。

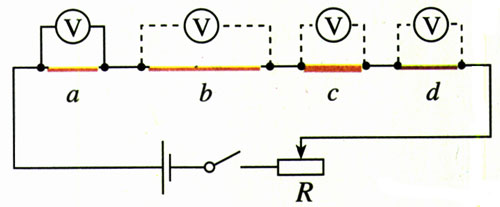
图中四段导体是串联的，每段导体两端的电压与它们的电阻成正比，因此，用电压表分别测量a、b、c、d两端的电压，就能知道它们的电阻之比。

比较a、b的电阻之比与它们的长度之比；比较a、c的电阻之比与它们的横截面积之比；比较a、d的电阻是否相等。这样就可以得出长度、横截面积、材料这三个因素与电阻的关系。

改变滑动变阻器滑片的位置，可以获得多组实验数据以得到更可靠的结论。

这个实验得到的是电阻与导线长度、横截面积的比例关系，实验中不必测量电阻大小的数值。

探究方案二

除了上述探究思路外，我们还可以用刚刚学过的知识，通过逻辑推理来探究导体的电阻与导体长度、横截面积的关系，然后通过实验来探究导体电阻与材料的关系。

1．分析导体电阻与它的长度的关系

一条长度为l、电阻为R的导体，可以看成是由n段长度同为l₁、电阻同为R₁的导体串联而成的，这n段导体的材料、横截面积都相同。总长度l与每段长度l₁的关系为

\(\frac{l}{{{l_1}}}\)＝n

另一方面，由串联电路的性质可知，R＝nR₁，即

\(\frac{R}{{{R_1}}}\)＝n

对比两式，可知

\(\frac{R}{{{R_1}}}\)＝\(\frac{l}{{{l_1}}}\)

即在横截面积、材料相同的条件下，导体的电阻与长度成正比。

2．研究导体电阻与它的横截面积的关系

有n条导体，它们的长度相同、材料相同、横截面积相同。横截面积同为S₁、电阻同为R₁。把它们紧紧地束在一起，组成一根横截面积为S、电阻为R的导体。

由并联电路的性质可知，R＝\(\frac{R_1}{n}\)，即

\(\frac{R_1}{R}\)＝n

同时

\(\frac{S}{S_1}\)＝n

所以

\(\frac{R}{R_1}\)＝\(\frac{S_1}{S}\)

即在长度、材料相同的条件下，导体的电阻与横截面积成反比。

在以上两个结论的基础上，再通过实验探究导体的电阻是否跟材料有关，这时对它们的几何尺寸就可以不做限制。这样实验操作的自由度就大多了。

实验

探究导体电阻与材料的关系

1．根据以上分析，以等式的形式写出用导体长度l、导体横截面积S表示导体电阻R的关系式，用一个与l、S无关的常量表示比例系数。

2．选择至少两种不同材料的导体（例如镍铬合金丝和康铜丝），测出它们的长度、横截面积和电阻，分别计算出上述等式中的比例系数。

3．分析上述比例系数的物理意义。

电阻定律

同种材料的导体，其电阻R与它的长度l成正比，与它的横截面积S成反比；导体电阻与构成它的材料有关。这就是电阻定律，写成公式，则是

R＝ρ\(\frac{l}{S}\)                （1）

式中ρ是比例系数，它与导体的材料有关，是表征材料性质的一个重要的物理量。在长度、横截面积一定的条件下，ρ越大，导体的电阻越大。ρ叫做这种材料的电阻率（resistivity）。

思考与讨论

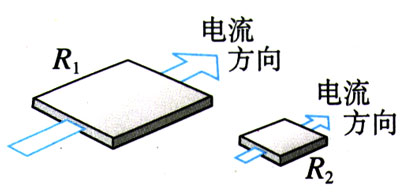
图2.6-4中，R₁和R₂是材料相同、厚度相同、表面为正方形的导体，但R₂的尺寸比R₁小很多。通过两导体的电流方向如图所示。这两个导体的电阻有什么关系？

你认为这种关系对电路元件的微型化有什么意义？

*锰铜合金：85%铜，3%镍，12%锰。

**镍铜合金：54%铜，46%镍。

***镍铬合金：67.5%镍，15%铬，16%铁，1.5%锰。

从上表中可以看出，纯净金属的电阻率较小，合金的电阻率较大。连接电路的导线一般用电阻率小的铝或铜来制作，必要时可在导线上镀银。

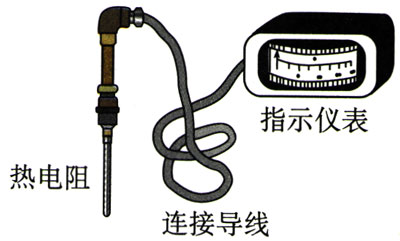
各种材料的电阻率一般都随温度的变化而变化。金属的电阻率随温度的升高而增大。电阻温度计（图2.6-5）就是利用金属的电阻随温度变化而制成的，可以用来测量很高的温度。精密的电阻温度计是用铂做的。已知铂丝的电阻随温度的变化情况，测出铂丝的电阻就可以知道温度。有些合金如锰铜合金和镍铜合金，电阻率几乎不受温度变化的影响，常用来制作标准电阻。

说一说

中央电视台2002年12月播放了北京市技术质量监督局对市场中电线电缆产品质量抽查的消息。消息引用检验负责人的话：“十几个不合格产品中，大部分存在导体电阻不合格问题，主要是铜材质量不合格，使用了再生铜或含杂质很多的铜。再一个就是铜材质量可能合格，但把截面积缩小，买2.5平方（毫米）的线，拿到手的线可能是1.5或1.5多一点的，载流量不够。还有一个问题是绝缘层质量不合格，用再生塑料制作电线外皮，电阻率达不到要求……”

谈一谈，这位负责人的讲话中体现了哪些物理原理？

问题与练习

1．在实验室用一段导线连接一个“3V、0.25 A“的小灯泡做实验时，一般都不会考虑导线的电阻。请你找一段这种导线，目测它的长度和导线中铜丝的横截面积，估算它的电阻，然后说明可以不考虑导线电阻的理由。

2．小李家的房子装修，买了一卷规格为“100 m、ϕ2.5 mm”的铜导线，用来安装一路专线，对额定功率1.5 kW的空调供电。实际上恰好用去了一半导线。如果空调能够正常工作，通电时在这段导线上损失的电压约是多少？

3．某同学想探究导电溶液是否与金属一样遵从电阻定律。她拿了一根自行车轮胎气门芯用的橡胶管，里面灌满了盐水，两端用粗铜丝塞住管口，形成一段封闭的盐水柱。她量得盐水柱的长度是30 cm，并测出盐水柱的电阻等于R。现握住橡胶管的两端把它拉长，使盐水柱的长度变为40 cm。如果溶液的电阻也遵从电阻定律，此时盐水柱的电阻应该等于多大？

4．有两根不同材料的金属丝，长度相同，甲的横截面的圆半径及电阻率都是乙的2倍。

（1）把它们并联在电路中，甲、乙消耗的电功率之比是多少？

（2）把它们串联在电路中，甲、乙消耗的电功率之比是多少？

发布时间：2017/4/18 下午9:32:32  阅读次数：972