第二章 4 串联电路和并联电路

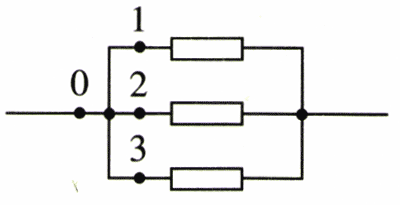
我们在初中已经知道，把几个导体依次首尾相连，接入电路，这样的连接方式叫做串联（series connection），如图2.4-1；把几个导体的一端连在一起，另一端也连在一起，然后把这两端接入电路，这样的连接方式叫做并联（parallel connection），如图2.4-2。这一节，我们分别研究串联电路和并联电路中各部分电流的关系、各部分电压的关系，以及各部分电阻的关系。

在初中，我们已经研究过其中的某些问题，现在用高中的物理知识做进一步分析。

串联电路和并联电路的电流

我们已经知道，恒定电流电路内各处电荷的分布是稳定的，任何位置的电荷都不可能越来越多或越来越少。在图2.4-1的串联电路中，要使串联电路中各处的电荷分布保持不变，相同时间内通过0、1、2、3各点的电荷量必须相等，因此，串联电路各处的电流相等，即

I₀＝I₁＝I₂＝I₃

在图2.4-2的并联电路中，只有在相同时间内流过干路0点的电荷量等于进入各支路1、2、3各点的电荷量之和，才能保持电路各处的电荷量的分布恒定不变。因此，并联电路的总电流等于各支路电流之和，即

I₀＝I₁＋I₂＋I₃

串联电路和并联电路的电压

在图2.4-1的串联电路中，如果以φ₀、φ₁、φ₂、φ₃分别表示电路中0、1、2、3各点的电势，以U₀₁、U₁₂、U₂₃、U₀₃分别表示0与1、1与2、2与3、0与3的电势差（即电压），那么从电势差跟电势的关系知道，

U₀₁＝φ₀－φ₁，U₁₂＝φ₁－φ₂，U₂₃＝φ₂－φ₃

因此

U₀₁＋U₁₂＋U₂₃＝φ₀－φ₃

另一方面

φ₀－φ₃＝U₀₃

所以

U₀₁＋U₁₂＋U₂₃＝U₀₃

即串联电路两端的总电压等于各部分电路电压之和。

在图2.4-2的并联电路中，不考虑导线的电阻，0、1、2、3各点之间没有电势差，它们具有相同的电势。同样，几个电阻右边的电势也相同，因此，并联电路的总电压与各支路电压相等。如果分别以U₁、U₂、U₃代表图2.4-2中三个电阻两端的电压，则

U₁＝U₂＝U₃＝U

串联电路和并联电路的电阻

两个电阻R₁、R₂串联起来接到电路里，作为一个整体，它相当于一个电阻（图2.4-3），这个电阻的大小与原来两个电阻的大小有什么关系？

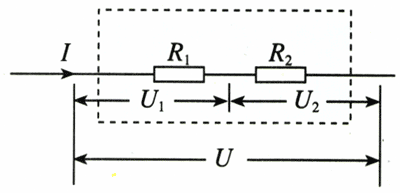
由于R₁与R₂是串联的，它们两端的总电压U等于两个电阻上的电压U₁、U₂之和，即

U＝U₁＋U₂

流过这两个电阻的电流I是一样的，上式两旁同除以电流I，于是得到

\(\frac{U}{I}\)＝\(\frac{{{U_1}}}{I}\)＋\(\frac{{{U_2}}}{I}\)

由欧姆定律，可得

R＝R₁＋R₂

不难证明，如果多个电阻串联，那么

R＝R₁＋R₂＋…

即串联电路的总电阻等于各部分电路电阻之和。

两个电阻R₁、R₂并联起来接到电路里，作为一个整体，它相当于一个电阻（图2.4-4），这个电阻的大小与原来两个电阻的大小有什么关系？

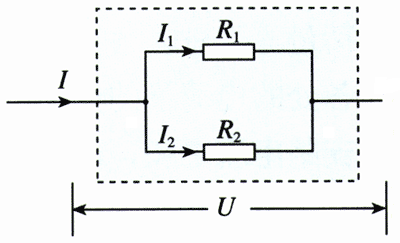
由于R₁与R₂是并联的，流过它们的总电流，等于两个电阻上的电流I₁，I₂之和，即

I＝I₁＋I₂

两个电阻上的电压U是相同的。把上式两旁同除以U，得

\(\frac{I}{U}\)＝\(\frac{{{I_1}}}{U}\)＋\(\frac{{{I_2}}}{U}\)

由欧姆定律，得

\(\frac{1}{R}\)＝\(\frac{1}{{{R_1}}}\)＋\(\frac{1}{{{R_2}}}\)

不难证明，如果多个电阻并联，那么

\(\frac{1}{R}\)＝\(\frac{1}{{{R_1}}}\)＋\(\frac{1}{{{R_2}}}\)＋…

思考与讨论

即并联电路总电阻的倒数等于各支路电阻的倒数之和。

试证明：

（1）n个相同的电阻并联，总电阻为一个电阻的n分之一；

（2）若干不同的电阻并联，总电阻小于其中最小的电阻。

电压表和电流表

常用的电压表和电流表都是由小量程的电流表G（表头）改装而成的。表头的工作原理涉及磁场对通电导线的作用，这是下一章学习的内容。从电路的角度看，表头就是一个电阻，同样遵从欧姆定律。表头与其他电阻的不同仅在于通过表头的电流是可以从刻度盘上读出来的。

电流表G的电阻R_g叫做电流表的内阻。指针偏转到最大刻度时的电流I_g叫做满偏电流。电流表G通过满偏电流时，加在它两端的电压U_g叫做满偏电压，由欧姆定律可知，U_g＝I_gR_g。

思考与讨论

图2.4-5是某一电流表G的刻度盘。使用时指针指着某一电流刻度，表示通过电流表的电流为某一数值，而且也意味着表头的两接线柱之间具有一定大小的电压，因此，电流表G实际上也是一个小量程的电压表。

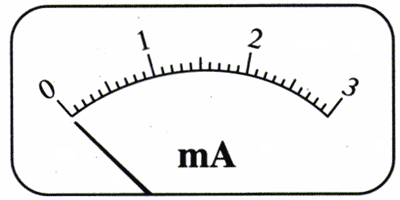
如果图中电流表的内阻是100 Ω，怎样在这个刻度盘上标出相应的电压数据？

表头的满偏电压和满偏电流一般都比较小，测量较大的电压时要串联一个电阻把它改装成电压表；测量较大的电流时则要并联一个电阻，把小量程的电流表改装成大量程的电流表。

【例题1】有一个电流表G，内阻R_g＝30 Ω满偏电流I_g＝1 mA。要把它改装为量程0～3 V的电压表，要串联多大的电阻？改装后电压表的内阻是多大？

【解】电压表V由表头G和电阻R串联组成，如图2.4-6的虚线框所示。电压表的量程是0～3 V，是指电压表V两端的电压为3 V时，表头的指针指在最大刻度，即通过电流表G的电流等于I_g。

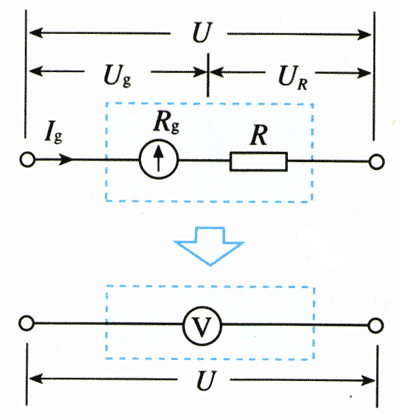
此时表头G两端得到的是满偏电压U_g＝I_gR_g＝0.03 V。电阻R分担的电压为U_R＝U－U_g＝2.97 V。

由欧姆定律可以求出分压电阻

R＝\(\frac{{{U_{\rm{R}}}}}{{{I_{\rm{g}}}}}\)＝\(\frac{{2.97}}{{1 \times {{10}^{ - 3}}}}\)Ω＝2.97×10³ Ω

电压表V的内阻等于R_g和R串联时的总电阻，即

R_V＝R_g＋R＝3.00×10³ Ω＝3.00 kΩ

也可以选择整个电压表为研究对象，根据欧姆定律由R_V＝\(\frac{U}{{{I_{\rm{g}}}}}\)求得电压表的内阻。

【例2】有一个电流表G，内阻R_g＝30 Ω，满偏电流I＝1 mA。要把它改装为量程0～0.6 A的电流表，要并联多大的电阻？改装后电流表的内阻是多大？

【解】电流表A由表头G和电阻R并联组成，如图2.4-7的虚线框所示。电流表量程为0～0.6 A，是指通过电流表A的电流为0.6A时，表头的指针指在最大刻度，即通过电流表G的电流等于I_g。

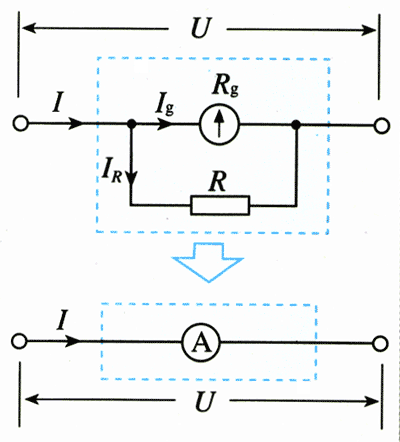
此时通过电阻R的电流I_R＝I－I_g＝（0.6－0.001）A＝0.599 A。由欧姆定律可以求出分流电阻

R＝\(\frac{U}{{{I_{\rm{R}}}}}\)＝\(\frac{{{I_{\rm{g}}}{R_{\rm{g}}}}}{{{I_{\rm{R}}}}}\)＝\(\frac{{1 \times {{10}^{ - 3}} \times 30}}{{0.599}}\)Ω＝0.050 Ω

电流表内阻R_A等于R_g与R的并联值。由

\(\frac{1}{{{R_{\rm{A}}}}}\)＝\(\frac{1}{{{R_{\rm{g}}}}}\)＋\(\frac{1}{R}\)

可以解出R_A，然后代入数据，得

R_A＝\(\frac{{{R_{\rm{g}}}R}}{{{R_{\rm{g}}} + R}}\)＝\(\frac{{30 \times 0.050}}{{30 + 0.050}}\)Ω＝0.050 Ω

也可以选择整个电流表为研究对象，根据欧姆定律由R_A＝\(\frac{U}{I}\)求得电流表的内阻。

问题与练习

1．（1）在图2.4-8中，电压之比\(\frac{{{U_1}}}{U}\)与电阻之比\(\frac{{{R_1}}}{{{R_1} + {R_2}}}\)有什么关系？

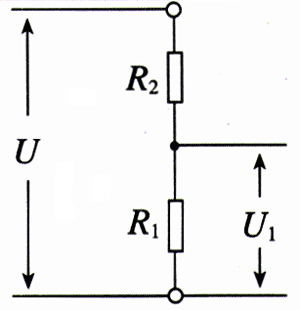
（2）图2.4-9的电路常称分压电路，当a、b间的电压为U时，利用它可以在c、d端获得0和U之间的任意电压。试说明其中的道理。

2．图2.4-10画出了用电压表，电流表测量导体电阻的两种电路图。

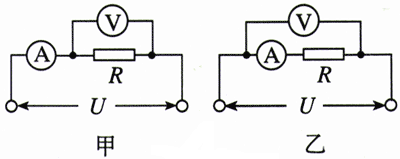
图中电压表的内阻为1 kΩ，电流表内阻为0.1 Ω，被测导体R的真实电阻为87.4 Ω。测量时，把电压表读数和电流表读数的比值作为电阻的测量值。

如果不考虑实验操作中的偶然误差，按甲、乙两种电路进行实验，得到的电阻测量值各是多少？你能从中得出什么结论？

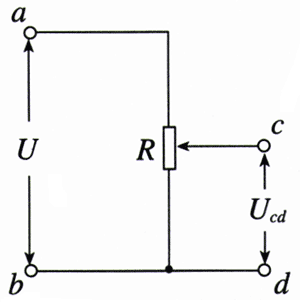
3．如图2.4-11，两个电阻串联后接在电路中a、b两点。已知a、b两点的电压能保持10 V不变。某同学把一个电压表并联在R₁两端时，电压表读数为5 V，将该电压表并联在R₂两端时，读数为4 V。两次电压表读数之和明显不等于串联电路的总电压，而实验用的电压表是正常的、准确的。这种现象可能发生吗？如果可能，分析产生这种现象的原因。

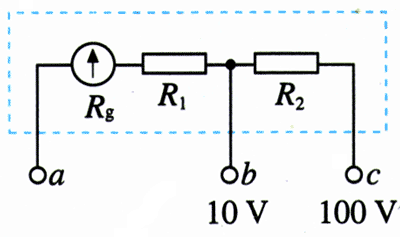
4．图2.4-12是有两个量程的电压泰，当使用a、b两个端点时，量程为0～10 V，当使用a、c两个端点时，量程为0～100 V。已知电流表的内阻R_g为500 Ω，满偏电流I_g为1 mA，求电阻R₁、R₂的值。

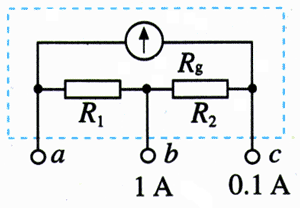
5．图2.4-13是有两个量程的电流表，当使用a、b两个端点时，量程为1 A，当使用a、c两个端点时，量程为0.1 A。已知表头的内阻R_g为200 Ω，满偏电流I_g为2 mA，求电阻R₁、R₂的值。

发布时间：2017/4/14 下午4:08:32  阅读次数：7276