第二章 3 欧姆定律
欧姆定律
电流的大小与什么因素有关?在初中我们曾经探究过导体中的电流跟导体两端电压、导体电阻的关系,现在我们进一步讨论这个关系。
演示
如图2.3-1,用电流表测量通过导体A的电流,用电压表测量A两端的电压。图中虚线框内是一个能提供可变电压的电路(其原理将在以后讨论,在此暂不涉及),调节滑动变阻器的滑片,可以得到关于导体A的几组电压、电流数据。随后,换用另一个导体B代替A进行实验,又可以得到关于导体B的多组电压、电流数据。
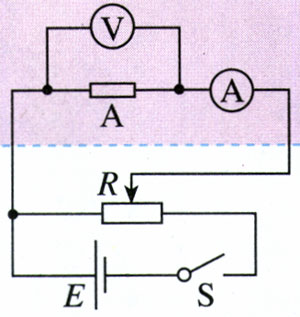
请你观察和记录实验数据,并在同一坐标系中作出A、B的U-I图象。
图2.3-2是根据某实验作出的关于金属导体A和B的U-I图象。从图中可以看出,同一金属导体的U-I图象是一条过原点的直线。这表明,同一导体,不管电流、电压怎样变化,电压跟电流的比值都是一个常数,此结论可写为
R=\(\frac{U}{I}\)
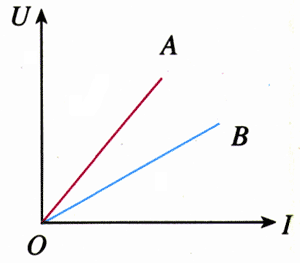
R是一个只跟导体本身性质有关而与通过的电流无关的物理量。图中不同导体U-I图象的倾斜程度不同,表明不同导体的R值不同。从以上公式可以看到,在电压U相同时,R越大的导体电流I越小。看来R的值反映了导体对电流的阻碍作用,所以物理学中把它叫做导体的电阻(resistance)。有了电阻的概念,我们可以把电压、电流、电阻的关系写成
I=\(\frac{U}{R}\) (1)
上式可以表述为:导体中的电流跟导体两端的电压U成正比,跟导体的电阻R成反比。这就是我们在初中学过的欧姆定律(Ohm law)。
电阻的单位是欧姆(ohm),简称欧,符号是Ω。它是根据欧姆定律规定的:如果某段导体两端的电压是1 V,通过的电流是1 A,这段导体的电阻就是1 Ω,所以,1 Ω=1 V/A。常用的电阻单位还有千欧(kΩ)和兆欧(MΩ):
1 kΩ=103 Ω
1 MΩ=106 Ω
导体的伏安特性曲线
在实际应用中,常用纵坐标表示电流I、横坐标表示电压U,这样画出的I-U图象叫做导体的伏安特性曲线。某一个金属导体,在温度没有显著变化时,电阻是不变的,它的伏安特性曲线是通过坐标原点的直线,具有这种伏安特性的电学元件叫做线性元件。图2.3-2中导体A、B的伏安特性曲线如图2.3-3所示。
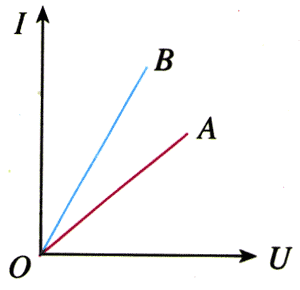
图2.3-2与图2.3-3看起来十分相像,不要混淆。
欧姆定律是个实验定律,实验中用的都是金属导体。这个结论对其他导体是否适用,仍然需要实验的检验。实验表明,除金属外,欧姆定律对电解质溶液也适用,但对气态导体(如日光灯管、霓虹灯管中的气体)和半导体元件并不适用。也就是说,在这些情况下电流与电压不成正比,这类电学元件叫做非线性元件。
实验
测绘小灯泡的伏安特性曲线
实验装置如图2.3-4,L为额定电流0.2 A左右的小灯泡,虚线框内是能够提供可变电压的电路。开关闭合前,调节滑动变阻器的滑片,使它靠近电路图中变阻器左端的接线柱,这时小灯泡两端的电压为零。
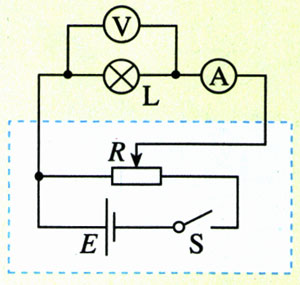
闭合开关后逐渐移动变阻器的滑片,增加小灯泡两端的电压,从零开始记录电流表和电压表的多组读数,直至电流达到它的额定电流为止。
根据实验数据在方格纸上作出小灯泡灯丝的伏安特性曲线。也可以把测量数据输入计算机中,利用数表软件直接生成伏安特性曲线。
你在自己得到的曲线中有什么新的发现?你怎样解释这个发现?
说一说
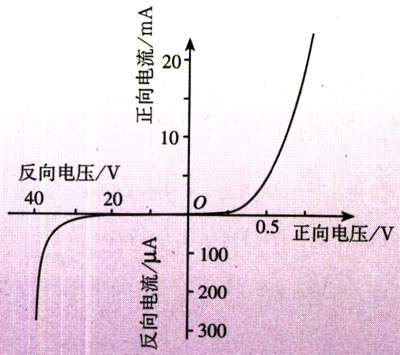
图2.3-5是某晶体二极管的伏安特性曲线,请你根据这条曲线说出通过二极管的电流与二极管两端电压的关系。
问题与练习
1.某电流表可以测量的最大电流是10 mA。已知一个电阻两端的电压是8 V时,通过的电流是2 mA,如果给这个电阻加上50 V的电压,能否用该电流表测量通过这个电阻的电流?
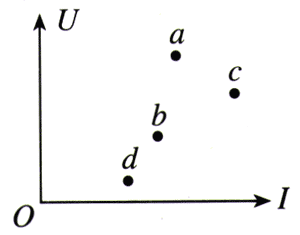
2.某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,得到了图2.3-6中a、b、c、d四个点。请比较这四个电阻值的大小。
3.有三个电阻:RA=5 Ω,RB=10 Ω,RC=2.5 Ω,它们的伏安特性曲线都是过原点的直线。请在同一坐标系中作出它们的伏安特性曲线,并在线旁标明A,B,C。
4.一个小灯泡,当它两端的电压在3 V以下时,电阻大致等于14 Ω不变;当它两端电压增大到4 V时,钨丝温度明显升高,它的电阻为16 Ω;当电压增大到5 V时,它的电阻为20 Ω。它在0~5V范围内的伏安特性曲线大概是怎样的?请画出草图。
5.初中数学课中已经学过,正比例函数可以表示为y=kx的形式,它的图象是一条过原点的直线,k是直线的斜率。请证明:某导体伏安特性曲线的斜率等于这个导体的电阻的倒数。
文件下载(已下载 164 次)发布时间:2017/4/12 下午2:46:54 阅读次数:2383
