第一章 9 带电粒子在电场中的运动

带电粒子在电场中受到静电力的作用，因此要产生加速度，速度的大小和方向都可能发生变化。对于质量很小的带电粒子，如电子、质子等，虽然它们也会受到万有引力（重力）的作用，但万有引力（重力）一般远小于静电力，可以忽略。

在现代科学实验和技术设备中，常常利用电场来改变或控制带电粒子的运动。利用电场使带电粒子加速、利用电场使带电粒子偏转，就是两种最简单的情况。

带电粒子的加速

如图1.9-1所示，在真空中有一对平行金属板，由于接上电池组而带电，两板间的电势差为U。若一个质量为m，带正电荷q的粒子，在静电力的作用下由静止开始从正极板向负极板运动，计算它到达负极板时的速度。

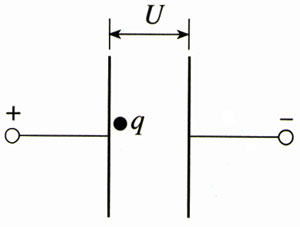
在带电粒子的运动过程中，静电力对它做的功是

W＝qU

设带电粒子到达负极板时的速率为v，其动能可以写为

E_k＝\(\frac{1}{2}\)mv²

由动能定理可知

\(\frac{1}{2}\)mv²＝qU

于是求出

v＝\(\sqrt {\frac{{2qU}}{m}} \)

思考与讨论

上述问题中，两块金属板是平行的，两板间的电场是匀强电场。如果两极板是其他形状，中间的电场不再均匀，上面的结果是否仍然适用？为什么？

【例题1】炽热的金属丝可以发射电子。在金属丝和金属板之间加以电压U＝2 500 V（图1.9-2），发射出的电子在真空中加速后，从金属板的小孔穿出。电子穿出时的速度有多大？设电子刚刚离开金属丝时的速度为零。

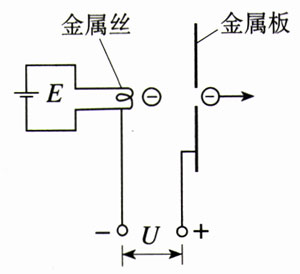
【解】电荷量为e的电子从金属丝移动到金属板，两处的电势差为U，电势能的减少量是eU。减少的电势能全部转化为电子的动能，所以

\(\frac{1}{2}\)mv²＝eU

解出速度v并把数值代入，得

v＝\(\sqrt {\frac{{2qU}}{m}} \)＝\(\sqrt {\frac{{2 \times 1.6 \times {{10}^{ - 19}} \times 2500}}{{0.9 \times {{10}^{ - 30}}}}}\)＝3.0×10⁷m/s

带电粒子的偏转

如图1.9-3所示，在真空中放置一对金属板Y和Yʹ，把两板接到电源上，于是两板间出现了电场。现有一个带电粒子射入电场，它受到的静电力的方向与速度方向不一致，因而发生偏转。下面通过例题做些深入的讨论。

【例题2】如图1.9-3，两个相同极板Y与Yʹ的长度l＝6.0 cm，相距d＝2 cm，极板间的电压U＝200 V。一个电子沿平行于板面的方向射入电场中，射入时的速度v₀＝3.0×10⁷ m/S。把两板间的电场看做匀强电场，求电子射出电场时沿垂直于板面方向偏移的距离y和偏转的角度θ。

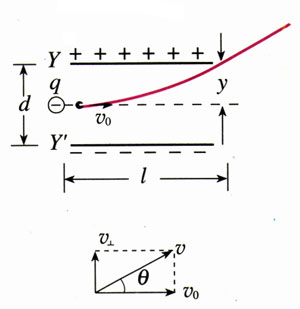
【解】电子在垂直于板面的方向受到静电力。由于电场不随时间改变，而且是匀强电场，所以整个运动中在垂直于板面的方向上加速度是不变的。加速度是

a＝\(\frac{F}{m}\)＝\(\frac{{eE}}{m}\)＝\(\frac{{eU}}{{md}}\)

电子射出电场时，在垂直于板面方向偏移的距离为

y＝\(\frac{1}{2}\)at²

其中t为飞行时间。由于电子在平行于板面的方向不受力，所以在这个方向做匀速运动，由l＝v₀t可求得

t＝\(\frac{l}{{{v_0}}}\)

将a和t代入y的表达式中，得到

y＝\(\frac{1}{2} \cdot \frac{{eU}}{{md}} \cdot {\left( {\frac{l}{{{v_0}}}} \right)^2}\)

代入数值后，得

y＝0.36 cm

即电子射出时沿垂直于板面的方向偏离0.36 cm。

由于电子在平行于板面的方向不受力，它离开电场时，这个方向的分速度仍是v₀，而垂直于板面的分速度是

v_⊥＝at＝\(\frac{{eU}}{{md}}\)·\(\frac{l}{{{v_0}}}\)

离开电场时的偏转角度θ可由下式确定

tanθ＝\(\frac{{{v_ \bot }}}{{{v_0}}}\)＝\(\frac{{eUl}}{{mdv_0^2}}\)

代入数值后，得

θ＝6.8°

带电粒子在匀强电场中的运动，跟重物在重力场中的运动相似，有时像自由落体运动，有时像抛体运动，依初速度是否为零而定。不过，重物在重力场中受到的力跟质量成正比，因此不同质量的物体具有相同的加速度（g）。但是带电粒子在电场中受到的力跟它的电荷量成正比，而电荷量相同的粒子可能质量不同，因而它们在电场中的加速度可以互不相同，这是静电场与重力场的重要区别。

示波管的原理

有一种电子仪器叫示波器，可以用来观察电信号随时间变化的情况。示波器的核心部件是示波管，图1.9-4是它的原理图。它由电子枪、偏转电极和荧光屏组成，管内抽成真空。电子枪的作用是产生高速飞行的一束电子，前面例题1实际上讲的就是电子枪的原理。

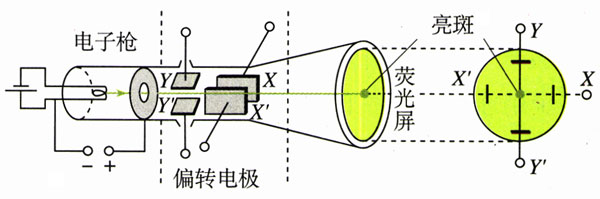
如果在偏转电极XXʹ之间和偏转电极YYʹ之间都没有加电压，电子束从电子枪射出后沿直线传播，打在荧光屏中心，在那里产生一个亮斑。

思考与讨论

1．如果在电极XXʹ之间不加电压，但在YYʹ之间加不变的电压，使Y的电势比Yʹ高（有时说这种情况是“Y正、Yʹ负”），电子束运动过程中受哪个方向的力？电子将打在荧光屏的什么位置？试着在图1.9-4中标出来。

如果在YYʹ之间不加电压，而在XXʹ之间加不变的电压（X正、Xʹ负），电子将打在荧光屏的什么位置？试着在图1.9-4中标出来。

2．如果在电极XXʹ之间不加电压，而在电极YYʹ之间所加的电压按图1.9-5所示的规律随时间变化，在荧光屏上会看到什么图形？试着画出来。

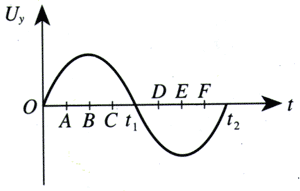
3．如果YYʹ之间的电压仍然如图1.9-5所示，而在电极XXʹ之间加不变的电压（X正、Xʹ负），在荧光屏上会看到什么图形？若XXʹ之间的电压是“X负、Xʹ正”呢？试着画出来。

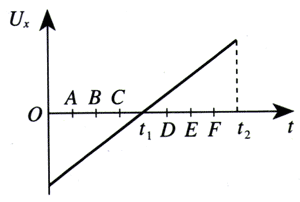
4．如果YYʹ之间的电压仍然如图1.9-5所示，而在电极XXʹ之间所加的电压按图1.9-6所示的规律变化，在荧光屏上会看到什么图形？建议按以下步骤画图。

（1）在白纸上按图1.9-6右侧的样子画出荧光屏的放大图；

（2）在图上分别标出O、A、B、C、t₁、D、E、F、t₂几个时刻光点在荧光屏上的位置；

（3）根据以上光点的位置，画出荧光屏上的图形。

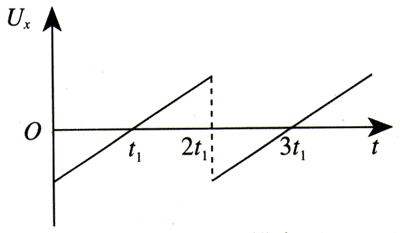
示波管的YYʹ偏转电极上加的是待显示的信号电压。这个电压是周期性的，XXʹ偏转电极通常接入仪器自身产生的锯齿形电压（图1.9-7），叫做扫描电压。如果信号电压是周期性的，并且扫描电压与信号电压的周期相同，就可以在荧光屏上得到待测信号在一个周期内随时间变化的稳定图象了。

科学足迹

密立根实验——电子电荷量的测定

在19世纪末发现电子以后，美国物理学家密立根（R．A．Millikan，1868-1953）在1907～1913年间进行了多次实验，比较准确地测定了电子的电量。

密立根并没有直接测量电子的电荷量，而是测定很小的带电油滴所带的电荷量。一个带电的油滴在匀强电场中所受的静电力是一定的。如果静电力的方向向上，并且大小正好与油滴所受的重力相等，那么油滴将悬浮在空间，由此可以测定油滴所带的电荷量。

图1.9-8是密立根实验的示意图。把两块水平放置的金属板分别与电源的正负极相接，板间产生匀强电场，方向竖直向下。用一个喷雾器把许多油滴从上板中间的小孔喷入电场。油滴从喷口出来时由于摩擦而带负电，在电场中受到向上的静电力。油滴的大小、质量、所带电荷量各不相同。在实验中要用显微镜来观察，找到悬浮不动的或做匀速直线运动的油滴，根据已知的电场强度从上述公式算出油滴的电荷量。这个实验操作难度较大，要求的精密度较高。

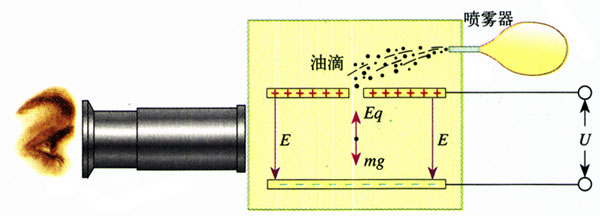
在进行了几百次测量以后，密立根发现油滴所带的电荷量虽不相同，但都是某个最小电荷量的整数倍，这个蕞小电荷量被认为是元电荷e，也就是电子的电荷量。

现代实验测出的电子电荷量是

e＝1.602 177 33×10^-19 C

到目前为止，科学实验尚未发现比这个电荷量更小的电荷。现代物理学家认为质子、中子等粒子是由更基本的成分——夸克组成的，夸克的电荷量为±\(\frac{1}{3}\)e或±\(\frac{2}{3}\)e。但是目前还没有找到独立存在的夸克，因而有的理论认为夸克是不能单独存在的，只能“集体”存在，其总电荷量为零或e。

在密立根的实验中，需要测量哪些物理量？请导出用这些物理量计算油滴电荷量的表达式。

科学漫步

范德格拉夫静电加速器

范德格拉夫（Van de Graaff，1901-1967）静电加速器由两部分组成，一部分是产生高电压的装置，叫做范德格拉夫起电机；另一部分是利用高电压加速带电粒子的加速管。

图1.9-9是起电机部分的示意图。金属球壳固定在绝缘支柱顶端，绝缘材料制成的传送带套在两个转轮上，由电动机带动循环运转。E和F是两排金属针（称做电刷）。

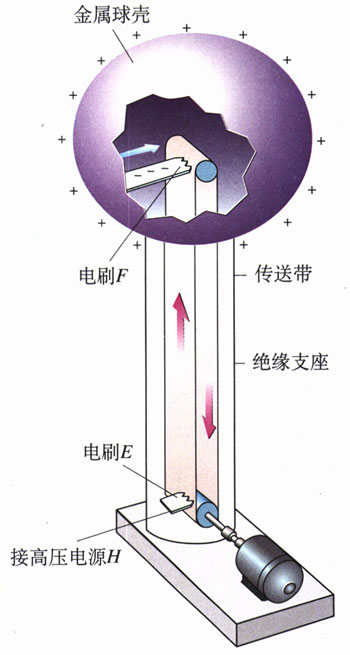
当电刷E与几万伏的直流高压电源H的正极接通时，E与大地之间就有几万伏的电势差。由于尖端放电，正电荷被喷射到传送带上，并被传送带带着向上运动。当正电荷到达电刷F附近时，F上被感应出异号电荷。由于尖端放电，F上的负电荷与传送带上的正电荷中和，从而使传送带失去电荷，而F上剩下了正电荷。由于导体带电电荷只能存在于外表面，所以F上的正电荷立即传到金属壳的外表面。这样，由于传送带的运送，正电荷不断从直流电源H接高压传到球壳的外表面，从而在金属壳与大地之间形成高电压。

由于电晕放电、局部尖端放电和漏电等现象，球壳与大地间的电压不能无限制提高。目前可达数百万伏。

带电粒子的加速是在加速管中进行的。加速管安装在起电机的绝缘支柱里面，管内抽成真空。管顶有离子发生装置，即粒子源，底部是靶。粒子源产生的正离子在强电场的作用下，经过加速可以获得很大的动能。由于粒子加速运动的轨迹是直线，这类加速器是一种直线加速器。

在医院，用直线加速器产生的粒子束（射线）治疗某些癌症，称为放射治疗。与使用钴60等放射性物质的放射治疗相比，使用直线加速器无需放射源，不开机时完全没有射线，更加安全，也便于管理。

问题与练习

1．真空中有一对平行金属板，相距6.2 cm，两板电势差为90V。二价的氧离子由静止开始加速，从一个极板到达另一个极板时，动能是多大？这个问题有几种解法？哪种解法比较简便？

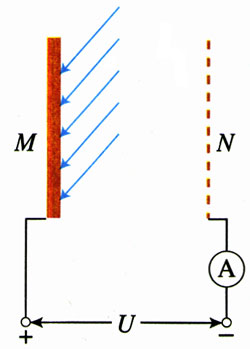
2．某种金属板M受到某种紫外线照射时会不停地发射电子，射出的电子具有不同的方向，其速度大小也不相同。在M旁放置一个金属网N。如果用导线将MN连起来，M射出的电子落到N上便会沿导线返回M，从而形成电流。现在不把M、N直接相连，而按图1.9-11那样在M、N之间加一个电压U，发现当U＞12.5 V时电流表中就没有电流。

问：被这种紫外线照射出的电子，最大速度是多少？

3．先后让一束电子和一束氢核通过同一对平行板形成的偏转电场。在下列两种情况下，分别求出电子偏角的正切与氢核偏角的正切之比。

（1）电子与氢核的初速度相同。

（2）电子与氢核的初动能相同。

4．让一价氢离子、一价氦离子和二价氦离子的混合物经过同一加速电场由静止开始加速，然后在同一偏转电场里偏转，它们是否会分离为三股粒子束？请通过计算说明。

5．电子从静止出发被1000 V的电压加速，然后沿着与电场垂直的方向进入另一个电场强度为5 000 N/C的匀强偏转电场，进入方向与电场强度方向垂直。已知偏转电极长6 cm，求电子离开偏转电场时的速度及其与进入偏转电场时的速度方向之间的夹角。

发布时间：2017/4/7 上午10:12:20  阅读次数：7726