第一章 4 电势能和电势
我们已经建立了电场强度的概念,知道它是描述电场性质的物理量。倘若把一个静止的试探电荷放入电场中,它将在静电力的作用下做加速运动,经过一段时间以后获得一定的速度,试探电荷的动能增加了。我们知道,这是静电力做功的结果,而功又是能量变化的量度,那么,在这一过程中,是什么能转化成试探电荷的动能呢?为此,我们首先要研究静电力做功的特点。
静电力做功的特点
试探电荷q在电场强度为E的匀强电场中沿几条不同路径从A点移动到B点(图1.4-1),我们计算这几种情况下静电力对电荷所做的功。
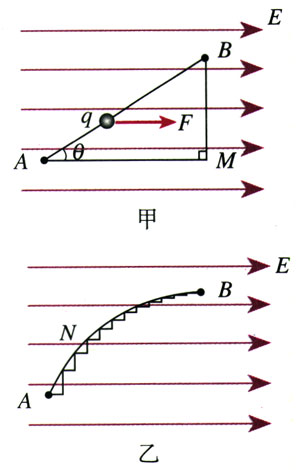
q在沿直线从A移往B的过程中(图1.4-1甲),受到的静电力F=qE,静电力与位移AB的夹角始终为θ,静电力对q所做的功为
W=Fcosθ·|AB|=qE·|AM|
q在沿折线AMB从A移往B的过程中(图1.4-1甲),在线段AM上静电力对q所做的功W1=qE·|AM|。在线段MB上,由于移动方向跟静电力垂直,静电力不做功,W2=0。在整个移动过程中静电力对q所做的功W=W1+W2。所以
W=qE·|AM|
再使q沿任意曲线ANB从A移动到B(图1.4-1乙)。我们可以用无数组跟静电力垂直和平行的折线来逼近曲线ANB。只要q的移动方向与静电力平行,静电力都做功,而这些与静电力平行的短折线的长度之和等于|AM|。因此,静电力所做的功还是
W=qE·|AM|
可见,不论q经由什么路径从A点移动到B点,静电力做的功都是一样的。因此,在匀强电场中移动电荷时,静电力做的功与电荷的起始位置和终止位置有关,但与电荷经过的路径无关。
这个结论虽然是从匀强电场中推导出来的,但是可以证明,对于非匀强电场也是适用的。
电势能
在必修物理课中我们学过,正是由于移动物体时重力做的功与路径无关,同一物体在地面附近的同一位置才具有确定的重力势能[1],从而也使重力势能的概念具有实际的意义。同样地,由于移动电荷时静电力做的功与移动的路径无关,电荷在电场中也具有势能,这种势能叫做电势能(electric potential energy或electrostatic potential energy),可用Ep表示。
思考与讨论
如果沿不同路径移动时静电力做的功不一样,还能建立电势能的概念吗?
物体在地面附近下降时,重力对物体做正功,物体的重力势能减少;物体上升时,重力对物体做负功,物体的重力势能增加。与此相似,当正电荷在电场中从A点移动到B点时,静电力做正功(图1.4-2甲),电荷的电势能减少;当电荷从B点移动到A点时,静电力做负功(图1.4-2乙),即电荷克服静电力做功,电荷的电势能增加。
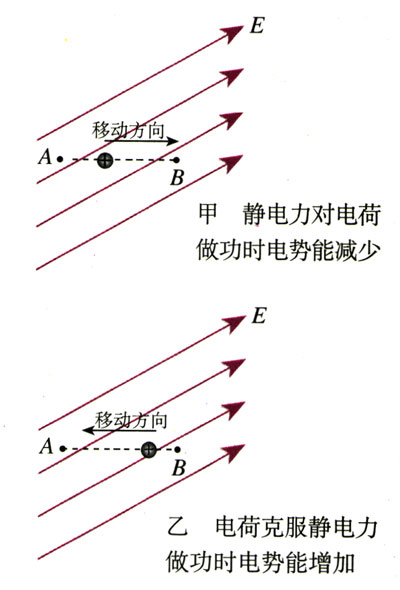
功是能量变化的量度。所以由上面的分析可以得出结论:静电力做的功等于电势能的减少量。若用WAB表示电荷从A点移动到B点的过程中静电力做的功,EpA和EpB分别表示电荷在A点和B点的电势能,则
WAB=EpA-EpB (1)
通过以上分析可以看到,静电力做的功只能决定电势能的变化量,而不能决定电荷在电场中某点的电势能的数值。只有先把电场中某点的电势能规定为零,才能确定电荷在电场中其他点的电势能。例如,若规定电荷在B点的电势能为零,则电荷在A点的电势能等于WAB。也就是说,电荷在某点的电势能,等于静电力把它从该点移动到零势能位置时所做的功。
通常把电荷在离场源电荷无限远处的电势能规定为零,或把电荷在大地表面上的电势能规定为零。
多么远是“无限远”?在静电问题中,如果离场源电荷已经很远,以至于试探电荷已经不能探测到电场了,这点就可以算是“无限远”。
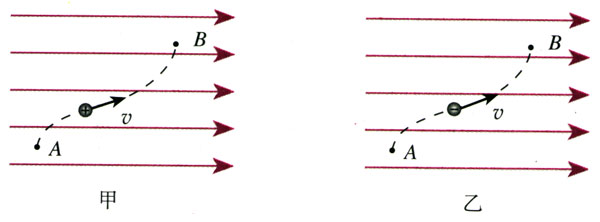
重力或引力存在的空间也称为重力场或引力场。物体在重力场或引力场中移动时,重力或引力做的功,跟电荷在电场中移动时静电力做的功虽然相似,但还是有很大的差异。这是由于存在两种电荷的缘故。在同一电场中,同样从A点到B点,移动正电荷与移动负电荷,电荷的电势能的变化是相反的(图1.4-3)。
电势
我们通过静电力的研究认识了电场强度,现在要通过电势能的研究来认识另一个物理量——电势,它同样是表征电场性质的重要物理量。
我们已经熟悉了用比值定义物理量的方法,现在就来研究电荷在电场中的电势能与它的电荷量的比值,从这里入手研究电势。
有一个电场强度为E场的匀强电场,如图1.4-4,规定电荷在O点的电势能为零。A为电场中的任意一点,电荷q在A点的电势能EpA等于电荷q由A点移至O点的过程中静电力做的功。由于静电力做功与路径无关,为方便起见,选择直线路径AO进行计算。设AO的长度为l,则EpA=qE场lcosθ。可见,电荷q在任意一点A的电势能EpA与q成正比。也就是说,处于A点的电荷,无论电荷量大小是多少,它的电势能跟电荷量的比值\(\frac{{{E_{{\rm{pA}}}}}}{q}\)都是相同的。对电场中的不同位置,由于l和θ可以不同,所以这个比值一般是不同的。
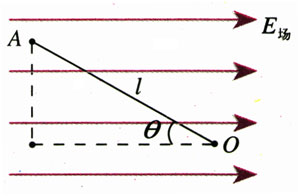
按照国家标准,电场强度和能量都用字母E表示,而在本节,电场强度和能量会在同一个关系式中出现。为了区分,我们用E场表示电场强度,用Ep表示势能,在某点A的势能用EpA表示。
从以上分析可知,电荷在电场中某一点的电势能与它的电荷量的比值,是由电场中这点的性质决定的,跟试探电荷本身无关。这个结论虽然是从匀强电场得出的,但可以证明,对于其他电场同样适用。
电荷在电场中某一点的电势能与它的电荷量的比值,叫做这一点的电势(electric potential)。如果用φ表示电势,用Ep表示电荷q的电势能,则
φ=\(\frac{{{E_{{\rm{p}}}}}}{q}\) (2)
在国际单位制中,电势的单位是伏特(volt),符号为V。在电场中的某一点,如果电荷量为1 C的电荷在该点的电势能是1 J,这一点的电势就是1 V,即1 V=1 J/C。
在图1.4-4中,假如正的试探电荷沿着电场线从左向右移向O点,它的电势能逐渐减少,电势逐渐降低,因此,电场线指向电势降低的方向。
与电势能的情况相似,应该先规定电场中某处的电势为零,然后才能确定电场中其他各点的电势。在物理学的理论研究中常取离场源电荷无限远处的电势为零,在实际应用中常取大地的电势为零[2]。
在规定了电势零点之后,电场中各点的电势可以是正值,也可以是负值。
电势只有大小,没有方向,是个标量。
思考与讨论
在上面关于电势能和电势的讨论及插图中,我们一直把试探电荷q当做正电荷处理。请把q当做负电荷,重复以上讨论。其结果与上面的结果是否一致?
等势面
在地图中常用等高线来表示地势的高低。与此相似,在电场的图示中常用等势面来表示电势的高低。
电场中电势相同的各点构成的面叫做等势面(equipotential surface)。与电场线的功能
相似,等势面也是用来形象地描绘电场的。等势面与电场线有什么关系呢?
在同一个等势面上,任何两点间的电势都相等。所以在同一等势面上移动电荷时静电力不做功。由此可知,等势面一定跟电场线垂直,即跟电场强度的方向垂直。这是因为,假如不垂直,电场强度就有一个沿着等势面的分量,在等势面上移动电荷时静电力就要做功,这个面也就不是等势面了。
这里讨论等势面与电场线的关系时用到了反证法。反证法是科学研究中重要的逻辑方法,在日常生活中也常用到。你能举出一些例子吗?
前面说过,沿着电场线的方向,电势越来越低。总起来说,就是:电场线跟等势面垂直,并且由电势高的等势面指向电势低的等势面。
图1.4-5是几种电场的等势面和电场线。每幅图中,两个相邻的等势面间的电势之差是相等的。
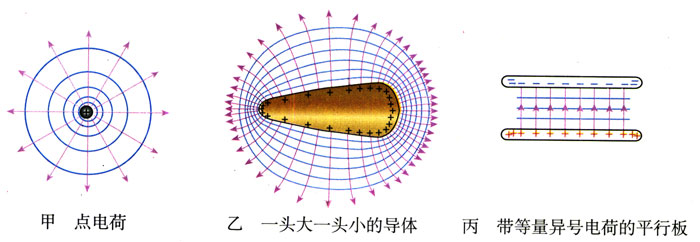
实际测量电势比测量电场强度容易,所以常用等势面研究电场。先测绘出等势面的形状和分布,再根据电场线与等势面的关系,绘出电场线的分布,于是就知道电场的情况了。设计电子仪器(如示波管、电子显微镜等)中电极的形状、大小和相互位置时,都要利用试验模型测绘等势面的形状和分布,推知电极产生的电场的情况,以便确定符合实际要求的设计方案。
问题与练习
1.把q1=4×10-9 C的试探电荷放在电场中的A点,具有6×10-8 J的电势能,求A点的电势。若把q2=2×10-10 C的试探电荷放在电场中的A点,电荷所具有的电势能是多少?
2.解答以下题目后进行小结:如何根据试探电荷的电势能来判断电场中两点电势的高低?
(1)+q在A点的电势能比在B点大,A、B两点哪点电势高?
(2)-q在C点的电势能比在D点大,C、D两点哪点电势高?
(3)+q在E点的电势能为负值,-q在F点的电势能也是负值,E、F两点哪点电势高?
3.根据图1.4-6解答以下题目,然后进行小结:如何根据电场线来判断电场中两点电势的高低?
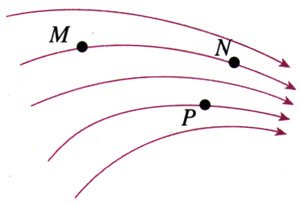
(1)M、N是同一条电场线上的两点,哪点电势高?
(2)M、P是同一电场中不在同一条电场线上的两点,哪点电势高?
4.在重力场中可以把物体的重力势能与它的质量的比值定义为重力势。如果物体在地面上的重力势能为零,试写出重力势的表达式。
5.以无限远处的电势为零,请把点电荷+Q、-Q电场中某一点P产生的电势及试探电荷+q、-q在P点的电势能的特点填在以下表格中。
|
场源电荷 |
P点电势φP的正负 |
+q在P点的电势能E+q的正负 |
-q在P点的电势能E-q的正负 |
当P点移至离场源电荷较近的位置时 |
||
|
φP怎样变化 |
E+q怎样变化 |
E-q怎样变化 |
||||
|
+Q |
|
|
|
|
|
|
|
-Q |
|
|
|
|
|
|
6.电场中两个电势不同的等势面能不能相交?说明理由。
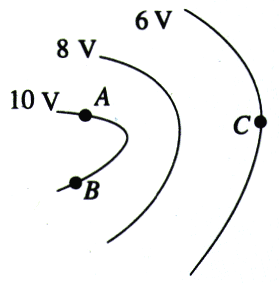
7.某电场的等势面如图1.4-7所示,试画出电场线的大致分布。若单位正电荷q沿任一路径从A点移到B点,静电力所做的功是多少?说明理由。正电荷q从A点移到C点,跟从B点移到C点,静电力所做的功是否相等?说明理由。
发布时间:2017/3/28 上午10:29:16 阅读次数:10446
