第十七章 2 科学的转折:光的粒子性
光究竟是什么?这似乎不应再是一个问题。因为从19世纪初开始,托马斯·杨、菲涅耳、马吕斯等分别观察到了光的干涉、衍射和偏振现象,这等于对微粒说宣判了死刑。19世纪60年代和80年代,麦克斯韦和赫兹先后从理论上和实验上确认了光的电磁波本质,光的波动理论似乎已经完美了。
既然如此,为什么又要谈论“光的粒子性”呢?
不断发现和认识新现象,进而理解事物的本性,这是一切科学发展的必由之路。人类对光的研究也是如此。重新提出“光的粒子性”,恰恰展示了曲折的认识过程。科学在这里又一次转折……
演示
把一块锌板连接在验电器上,用紫外线灯照射锌板(图17.2-1),观察验电器指针的变化。
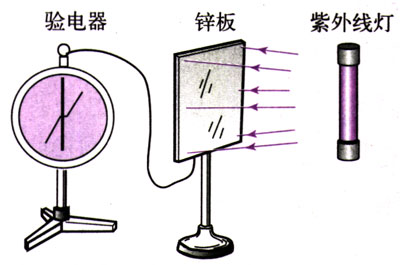
这个现象说明了什么问题?
光电效应的实验规律
1887年,赫兹在研究电磁波的实验中偶尔发现,接收电路的间隙如果受到光照,就更容易产生电火花。这就是最早发现的光电效应,也是赫兹细致观察的意外收获。后来这一现象引起许多物理学家的关注。德国物理学家P.勒纳德(P.Lenard)、英国物理学家J.J.汤姆孙(J.J.Thomson,1856-1940)等相继进行了实验研究,证实了这个现象,即照射到金属表面的光,能使金属中的电子从表面逸出。这个现象称为光电效应(photoelectric effect)。
可以用图17.2-2的电路研究光电效应中电子发射的情况与照射光的强弱、光的颜色(频率)等物理量间的关系。阴极K和阳极A是密封在真空玻璃管中的两个电极,K在受到光照时能够发射光电子。K与A之间电压的大小可以调整,电源的正负极也可以对调。电源按图示极性连接时,阳极A吸收阴极K发出的光电子,在电路中形成光电流。
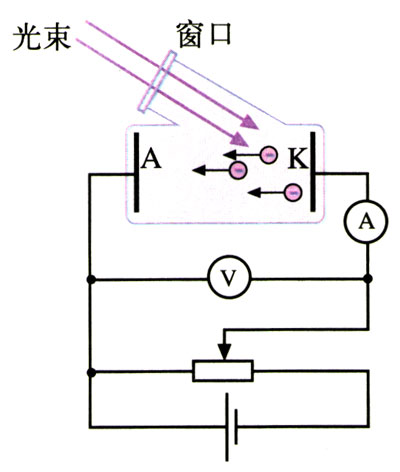
实验发现了以下规律。
存在着饱和电流
在光照条件不变的情况下,随着所加电压增大,光电流趋于一个饱和值。也就是说,在电流较小时电流随着电压的增大而增大;但当电流增大到一定值之后,即使电压再增大,电流也不会增大了,如图17.2-3所示。
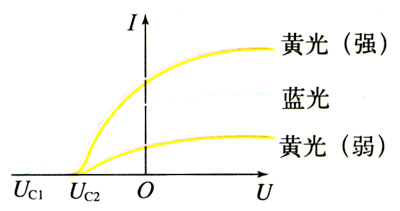
这说明,在一定的光照条件下,单位时间内阴极K发射的光电子的数目是一定的,电压增加到一定值时,所有光电子都被阳极A吸收,这时即使再增大电压,电流也不会增大。
实验表明,入射光越强,饱和电流越大。这表明入射光越强,单位时间内发射的光电子数越多。
存在着遏止电压和截止频率
当所加电压U为零时,电流I并不为零。只有施加反向电压,也就是阴极接电源正极、阳极接电源负极,在光电管两极间形成使电子减速的电场,电流才有可能为零。使光电流减小到零的反向电压Uc称为遏止电压。遏止电压的存在意味着光电子具有一定的初速度。众多光电子的初速度不一定一样,它的上限vc应该满足以下关系
\(\frac{1}{2}\)mevc2=eUc (1)
实验表明,对于一定颜色(频率)的光,无论光的强弱如何,遏止电压都是一样的。光的频率ν改变时,遏止电压Uc也会改变,如图17.2-3所示。这表明光电子的能量只与入射光的频率有关,而与入射光的强弱无关。
从实验中还可以看出,当入射光的频率减小到某一数值νc时,即使不施加反向电压也没有光电流,这表明已经没有光电子了。νc称为截止频率(cutoff frequency)或极限频率。这就是说,当入射光的频率低于截止频率时不能发生光电效应。实验表明,不同金属的截止频率不同。
光电效应具有瞬时性
当频率超过截止频率νc时,无论入射光怎样微弱,几乎在照到金属时立即产生光电流。精确测量表明产生电流的时间不超过10-9 s,即光电效应几乎是瞬时的。
光电效应解释中的疑难
光的电磁理论只能部分地解释光电效应。
人们知道,金属中原子外层的价电子会脱离原子而做无规则的热运动。但在温度不很高时,电子并不能大量逸出金属表面,这表明金属表面层内存在一种力,阻碍电子的逃逸。电子要从金属中挣脱出来,必须克服这种阻碍做功。使电子脱离某种金属所做功的最小值,叫做这种金属的逸出功(work function),用W0表示。不同金属的逸出功不同,见表1。
|
表1 几种金属的逸出功和极限频率[1] |
|||||
|
金属 |
钨 |
钙 |
钠 |
钾 |
铷 |
|
νc/ 1014 Hz |
10.95 |
7.73 |
5.53 |
5.44 |
5.15 |
|
W0/ eV |
4.54 |
3.20 |
2.29 |
2.25 |
2.13 |
当光照射金属表面时,电子吸收能量。若电子吸收的能量与原有的热运动能量之和超过逸出功,电子就从表面逸出,这就是光电子。光越强,逸出的电子数越多,光电流也就越大。这些结论与实验相符。
但是,按照光的电磁理论,还应得出如下结论:①光越强,光电子的初动能应该越大,所以遏止电压Uc应该与光的强弱有关;②不管光的频率如何,只要光足够强,电子都可以获得足够能量以而逸出表面,不应存在截止频率;③如果光很弱,按经典电磁理论估算,电子需要几分钟到十几分钟的时间才能获得逸出表面所需的能量,这个时间远远大于10-9 s。这些结论与实验结果相矛盾。此外,对于遏止电压Uc与光的频率ν的关系,经典电磁理论更是无法解释。
众多的疑难呼唤着新的思想、新的观念、新的理论。
爱因斯坦的光电效应方程
普朗克的能量子假说是对经典物理学思想与观念的一次突破,连普朗克本人都很犹豫,多数物理学家自然更难接受。所以在开始的几年里它没有受到重视,物理学界几乎没有去讨论它。最早认识到能量子意义的是年轻的爱因斯坦,他在1905年发表了《关于光的产生和转化的一个试探性观点》一文。他表示,普朗克关于辐射问题的崭新观点还不够彻底,仅仅认为电磁波在吸收和辐射时才显示出不连续性,这还不够,实际上电磁辐射本身就是不连续的,也就是说,光不仅在发射和吸收时能量是一份一份的,而且光本身就是由一个个不可分割的能量子组成的,频率为ν的光的能量子为hν,h为普朗克常量。这些能量子后来称为光子(photon)。
常温下金属中电子的热运动能量约为4×10-2 eV,比产生光电效应的光子能量hν(约75 eV)小得多,可以忽略。
按照爱因斯坦的理论,在光电效应中,金属中的电子吸收一个光子获得的能量是hν,这些能量的一部分用来克服金属的逸出功W0,剩下的表现为逸出后电子的初动能Ek,即
hν=Ek+W0
或
Ek=hν-W0 (2)
式中Ek为光电子的最大初动能,Ek=\(\frac{1}{2}\)mev2。
电子吸收光子后从金属中逸出时,除了要做逸出功外,有时还要克服原子的其他束缚而做功,这时光电子的初动能就比(2)式中的Ek小。因此,以下把Ek称做“最大”初动能。
上面(2)式称为爱因斯坦光电效应方程。从下面的讨论可以看出,这个方程使得光电效应中理论与实验的矛盾迎刃而解。
- 爱因斯坦方程表明,光电子的最大初动能Ek与入射光的频率ν有关,而与光的强弱无关。只有当hν>W0时,才有光电子逸出,νc=\(\frac{W_0}{h}\)就是光电效应的截止频率。
- 电子一次性吸收光子的全部能量,不需要积累能量的时间,光电流自然几乎是瞬时产生的。
- 光较强时,包含的光子数较多,照射金属时产生的光电子较多,因而饱和电流较大。
爱因斯坦提出光电效应的解释时,实验测量尚不精确,加上这种观点与以往的观点大相径庭,因此并未立即得到承认,甚至被说成是“在思辨中迷失目标”的“冒昧的假设”。
从1907年起,美国物理学家密立根(R.A.Millikan,1868 - 1953)开始以精湛的技术测量光电效应中几个重要的物理量。他后来写道:“经过十年之久的实验……与我自己的预料相反,这项工作终于成了爱因斯坦方程式在很小误差范围内的直接实验证据。”爱因斯坦也由于发现了光电效应的规律而获得1921年的诺贝尔物理学奖。
光子像其他粒子一样,也具有能量。光电效应显示了光的粒子性。
在本节稍后的部分我们将会看到,光子像其他粒子一样,不但具有能量,也具有动量。
思考与讨论
爱因斯坦光电效应方程给出了光电子的最大初动能Ek与入射光的频率ν的关系。但是,很难直接测量光电子的动能,容易测量的是遏止电压Uc。怎样根据(1)、(2)两式得到Uc与ν、W0的关系?
【例题】密立根的实验的目的是:测量金属的遏止电压Uc与入射光频率ν,由此算出普朗克常量h,并与普朗克根据黑体辐射得出的h相比较,以检验爱因斯坦方程式的正确性。
实验结果是,两种方法得出的普朗克常量h在0.5%的误差范围内是一致的。下表是某次实验中得到的某金属的Uc和ν的几组对应数据。
|
Uc/V |
0.541 |
0.637 |
0.714 |
0.809 |
0.878 |
|
ν/1014 Hz |
5.644 |
5.888 |
6.098 |
6.303 |
6.501 |
试作出Uc-ν图象并通过图象求出:
(1)这种金属的截止频率;
(2)普朗克常量。
【分析】本节(1)式可以写成
Ek=eUc (3)
它给出了光电子的最大初动能Ek与遏止电压Uc的关系。(2)式则给出了最大初动能Ek与光的频率ν的关系。(3)式和(2)式结合,消去Ek,解出Uc,得到
Uc=\(\frac{h}{e}\)ν-\(\frac{W_0}{e}\) (4)
本题中逸出功W0是确定的,电子电荷e和普朗克常量h都是常量。所以,(4)式表明遏止电压Uc与光的频率ν之间是一次函数的关系,即线性关系,Uc-ν图象是一条斜率为\(\frac{h}{e}\)的直线。
初中数学已经学过,形式为y=kx+b的一次函数图象是一条斜率为k的直线。
遏止电压Uc与光电子的最大初动能有关,最大初动能越大,遏止电压越高;如果遏止电压为零,表示光电子的最大初动能也是零,即没有光电子。与遏止电压Uc=0对应的频率应该是截止频率νc。
Uc-ν直线的斜率可以从图中测量,因此作出图象就能求出h。
【解】以频率ν为横轴,以遏止电压Uc为纵轴,根据表中数据选取适当比例,描点后作直线拟合这些点,得到Uc-ν图象如图17.2-4所示。
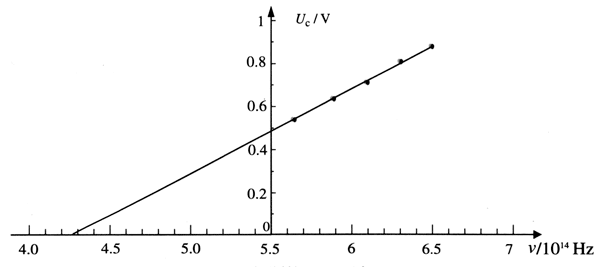
为了作图的方便,图17.2-4中两个坐标轴的交点没有选在原点,读图时要注意。
(l)前面(4)式中Uc=0对应的频率ν即为截止频率,从图象上看,Uc=0的点就是直线与横轴的交点。由图读出,这种金属的截止频率为
νc=4.27×1014 Hz
(2)在图中选取两个与直线偏离最小的点,即表中第1列和第5列数据,由它们计算直线的斜率\(\frac{h}{e}\)
\(\frac{h}{e}\)=\(\frac{{\Delta {U_c}}}{{\Delta \nu }}\)=×10-14 V·s=3.93×10-15 V·s
已知e=1.60×10-19 C,因而求得普朗克常量
h=6.30×10-34 J·s
思考与讨论
白天的天空各处都是亮的;航天员在大气层外飞行时,尽管太阳的光线耀眼刺目,其他方向的天空却是黑的,甚至可以看见星星。这是为什么?
康普顿效应
光在介质中与物质微粒相互作用,因而传播方向发生改变,这种现象叫做光的散射(scattering of light)。1918-1922年,美国物理学家康普顿(A.H.Compton,1892-1962)在研究石墨对X射线的散射时,发现在散射的X射线中,除了与入射波长λ0相同的成分外,还有波长大于λ0的成分,这个现象称为康普顿效应(Compton effect)。康普顿的学生,中国留学生吴有训(1897-1977)测试了多种物质对X射线的散射,证实了康普顿效应的普遍性。
按照经典物理学的理论,由于光是电磁振动的传播,入射光引起物质内部带电微粒的受迫振动,振动着的带电微粒从入射光吸收能量,并向四周辐射。这就是散射光。散射光的频率应该等于带电粒子受迫振动的频率,也就是入射光的频率,因而散射光的波长与入射光的波长应该相同,不会出现λ>λ0的散射光。经典理论与实验事实又一次出现了矛盾。
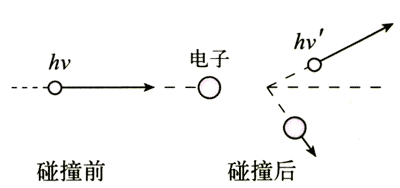
康普顿用光子的模型成功地解释了这种效应。他的基本思想是,X射线的光子不仅具有能量,也像其他粒子那样具有动量,X射线的光子与晶体中的电子碰撞时要遵守能量守恒定律和动量守恒定律,求解这些方程,可以得出散射光波长的变化值Δλ。理论结果与实验符合得很好。
光电效应和康普顿效应深入地揭示了光的粒子性的一面。前者表明光子具有能量,后者表明光子除了能量之外还具有动量。康普顿因此获得了1927年的诺贝尔物理学奖。
光子的动量
在狭义相对论中我们已经知道,一定的质量m与一定的能量E相对应:E=mc2。一个光子的能量是hν,即hν=mc2,所以它的质量是m=\(\frac{{h\nu }}{{{c^2}}}\)。借用质子、电子等粒子动量的定义:动量=质量×速度,可得光子的动量
这里得出的光子质量是它的相对论质量。由于光子不能静止下来,所以它没有静止质量。
p=mc=\(\frac{{h\nu }}{{{c^2}}}\)·c=\(\frac{{h\nu }}{c}\)
考虑到
\(\frac{c}{\nu}\)=λ
所以,光子的动量为
p=\(\frac{h}{\lambda }\)
你是否已经注意到,光子的能量表达式ε=hν与动量表达式p=h/λ具有高度对称性!
在康普顿效应中,当入射的光子与晶体中的电子碰撞时,要把一部分动量转移给电子,因而光子动量变小。从p=\(\frac{h}{\lambda }\)看,动量p减小意味着波长λ变大,因此有些光子散射后波长变大。从动量守恒定律和能量守恒定律出发,按照动量表达式p=\(\frac{h}{\lambda }\)和能量表达式ε=hν对康普顿效应做定量分析,其结论与实验事实符合得很好。
问题与练习
1.在可见光范围内,哪种颜色光的光子能量最大?想想看,这种光是否一定最亮?为什么?
2.在光电效应实验中
(1)如果入射光强度增加,将产生什么结果?
(2)如果入射光频率增加,将产生什么结果?
3.金属A在一束绿光照射下恰能产生光电效应,现用紫光或红光照射时,能否产生光电效应?紫光照射A、B两种金属都能产生光电效应时,为什么逸出金属表面的光电子的最大速度大小不同?
4.铝的逸出功是4.2 eV,现在将波长200 nm的光照射铝的表面。
(1)求光电子的最大初动能。
(2)求遏止电压。
(3)求铝的截止频率。
5.根据图17.2-2所示的电路,利用能够产生光电效座的两种(或多种)频率已知的光来进行实验,怎样测出普朗克常量?根据实验现象说明实验步骤和应该测量的物理量,写出根据本实验计算普朗克常量的关系式。
6.假如一个光子与一个静止的电子碰撞,光子并没有被吸收,只是被电子反弹回来,散射光子的频率与原来光子的频率相比哪个大?为什么?
[1] 当金属表面涂敷其他物质时,逸出功会有显著改变。
发布时间:2017/3/15 下午1:39:15 阅读次数:5669
