第十三章 1 光的折射
固执于光的旧有理论的人们,最好是从它自身的原理出发,提出实验的说明。并且,如果他的这种努力失败的话,他应该承认这些事实。
——托马斯·杨[1]

光给了我们一个明亮的世界,可是它自己却像一团谜。人们不断争论着关于光的问题。光学既是物理学中一门古老的基础科学,又是现代科学领域中最活跃的前沿科学之一,具有强大的生命力和不可估量的发展前景。
按照不同的研究目的,光学可以粗略地分为两大分支:一支利用几何学的概念和方法研究光的传播规律,称为几何光学;另一支主要研究光的本性以及光与物质相互作用的规律,通常称为物理光学。我们先学习几何光学,然后学习物理光学。
光到底是什么?这个问题早就引起了人们的注意,不过在很长的时期内对它的认识却进展得很慢。
到17世纪时,科学界已经形成了两种学说:一种是微粒说,认为光是从光源发出的一种物质微粒,在均匀的介质中以一定的速度传播;另一种是波动说,是惠更斯首先提出的,认为光是在空间传播的某种波。微粒说和波动说都能解释一些光现象,但又不能解释当时观察到的全部光现象。
到了19世纪初,人们在实验中观察到了光的干涉和衍射现象,这是波动的特征,不能用微粒说解释,因而证明了波动说的正确性。19世纪60年代,麦克斯韦预言了电磁波的存在,并认为光也是一种电磁波。此后,赫兹在实验中证实了这种假说,这样,光的电磁说使光的波动理论发展到相当完美的地步,取得了巨大的成功。
但是,19世纪末又发现了新的现象——光电效应,这种现象用波动说无法解释。爱因斯坦于20世纪初提出了光子说,认为光具有粒子性,从而解释了光电效应。不过,这里所说的光子已经不同于过去所说的“微粒”了。
现在人们认识到,光既具有波动性,又具有粒子性。
第十三章 1 光的折射
折射定律
阳光能够照亮水中的鱼和水草,同时我们也能通过水面看到烈日的倒影,这说明:光从空气射到水面时,一部分光射进水中,另一部分先返回到空气中。一般说来,光从第1种介质射到它与第2种介质的分界面时,一部分光会返回到第1种介质,这个现象叫做光的反射(reflection);另一部分光会进入第2种介质,这个现象叫做光的折射(refraction)。
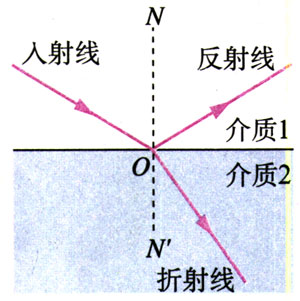
光从一种介质射到两种介质的分界面时发生反射,反射光线与入射光线、法线处在同一平面内,反射光线与入射光线分别位于法线的两侧;反射角等于入射角。这就是光的反射定律(reflection law)。
光在折射时遵循哪些规律呢?
如图13.1-2,让窄光束由一种介质斜射向另一种介质表面,例如,从空气射向水,或从水射向玻璃,我们研究入射光的折射情况。图中入射光线与法线间的夹角θ1叫做入射角,折射光线与法线间的夹角θ2叫做折射角。实验表明,当入射角变化时折射角随着改变。但是折射角与入射角之间有什么定量的关系呢?
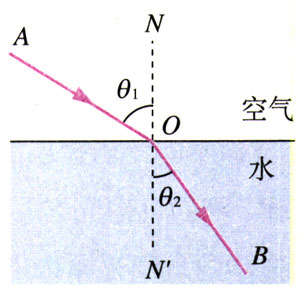
直到1621年,荷兰数学家斯涅耳在分析了大量数据后终于找到了两者之间的关系,并把它总结为光的折射定律(refraction law):折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比。即
\(\frac{{\sin {\theta _1}}}{{\sin {\theta _2}}}\)=n12 (1)
式中n12是比例常数。
说一说
我们在上一章研究波的折射时已经见过这个等式,那是从惠更斯原理得出的推论;而这里的(1)式是由实验得出来的。由此我们是否可以推测:光可能是一种波,我们常说的“光线”就是光波的波线?
所有事实都表明,在光的折射现象中,当光从水射向空气后(图13.1-2)也会发生偏折,而且光线沿BO的方向进入空气时,会沿OA的方向射出。也就是说,与光的反射现象一样,在光的折射现象中,光路也是可逆的。
光路可逆现象很有用处。例如,我们只对光从空气射入介质的情况做过深入的研究,但如果遇到光从介质射入空气的问题,由于光路可逆,也能得出结论。
折射率
光从第1种介质射人第2种介质时,入射角的正弦与折射角的正弦之比n12是个常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。在实际应用中,遇到最多的情形是光从空气射入某种介质,或从某种介质射入空气,而空气对光的传播的影响很小,可以作为真空处理。因此,以后我们只讨论光从真空射入介质的情形。这时,常数n12可以简单地记为n。
对于不同的介质来说,常数n是不同的。例如,光从空气射入水中时,n=1.33;光从空气射入某种玻璃时,n=1.50。可见常数n与介质有关系,是一个反映介质的光学性质的物理量。常数n越大,光线从空气斜射入这种介质时偏折的角度越大。
光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率(refractive index),用符号n表示。
研究表明,光在不同介质中的速度不同;某种介质的折射率,等于光在真空中的传播速度c与光在这种介质中的传播速度v之比,即
n=\(\frac{c}{v}\) (2)
(2)式也与惠更斯原理的结论一样。见第十二章第4节。
由于光在真空中的传播速度c大于光在任何其他介质中的传播速度v,因而任何介质的折射率n都大于1。所以,光从真空射入任何介质时,sinθ1都大于sinθ2,即入射角总是大于折射角。下表列出了几种介质的折射率
|
表1 几种介质的折射率 |
|||
|
介质 |
折射率 |
介质 |
折射率 |
|
金刚石 |
2.42 |
岩盐 |
1.55 |
|
二硫化碳 |
1.63 |
酒精 |
1.36 |
|
玻璃 |
1.5~1.8 |
水 |
1.33 |
|
水晶 |
1.55 |
空气 |
1.00028 |
说一说
光从介质1射入介质2(二者都不是真空),可能有几种折射情况?
实验
测定玻璃的折射率
如图13.1-3,当光以一定的入射角透过一块玻璃砖时,只要找出与入射光线AO相对应的出射光线O′D,就能够画出光从空气射入玻璃后的折射光线OO′,于是就能测量入射角θ1、折射角θ2。根据折射定律,就可以求出玻璃的折射率了。
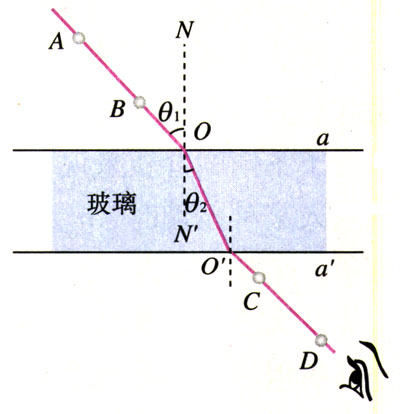
怎样确定与入射光线AO相对应的折射光线OO′?
把玻璃砖放在木板上,下面垫一张白纸,在纸上描出玻璃砖的两个边a和a′。然后,在玻璃砖的一侧插两个大头针A、B,AB的延长线与直线a的交点就是O。
眼睛在另一侧透过玻璃砖看两个大头针,使B把A挡住(图13.1-3)。如果在眼睛这一侧再插第三个大头针C,使它把A、B都挡住,插第四个大头针D,使它把前三个都挡住,那么后两个大头针就确定了从玻璃砖射出的光线。
在白纸上描出光线的径迹,测量相应的角度,就能计算玻璃的折射率了。
实验中,应该采取哪些措施以减小误差?
例题
如图13.1-4所示,一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶底上的点C,C、B两点相距\(\frac{d}{4}\)。求油的折射率和光在油中传播的速度。
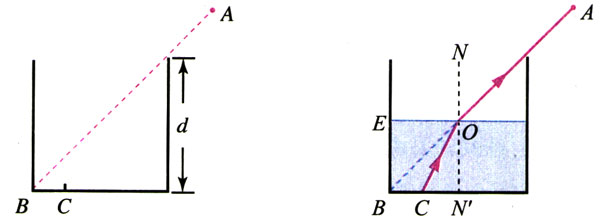
图13.1-4 计算油的折射率和油中的光速
【分析】在图乙中过直线AB与油面的交点O做油面的垂线,交桶底于N′点。此题是说,来自C点的光线沿CO到达油面后沿OA方向射入空气。折射现象中光路是可逆的,因此如果光线沿AO方向由空气射到油面,折射光将沿OC进入油中。以∠AON作为入射角,以么CON′作为折射角,由折射定律可以求出油的折射率n。
【解】因为底面直径与桶高相等,所以
∠AON=∠BON′=45°
由ON′=2CN′可知
sin∠CON′=\(\frac{{{\rm{CN'}}}}{{\sqrt {{\rm{C}}{{{\rm{N'}}}^2} + {\rm{O}}{{\rm{N}}^2}} }}\)=\(\frac{1}{{\sqrt 5 }}\)
因此,油的折射率
n=\(\frac{{\sin \angle {\mathop{\rm AON}\nolimits} }}{{\sin \angle {\rm{CON'}}}}\)=\(\frac{{\frac{{\sqrt 2 }}{2}}}{{\frac{1}{{\sqrt 5 }}}}\)=1.58
光在油中的传播速度
v=\(\frac{c}{n}\)=\(\frac{{3.0 \times {{10}^8}}}{{1.58}}\)m/s=1.9×108m/s
问题与练习
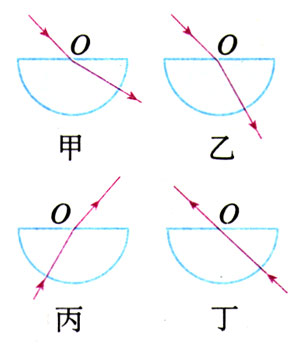
1.图13.1-5是光由空气射入半圆形玻璃砖,再由玻璃砖射入空气的光路图,O点是半圆形玻璃砖的圆心。指出哪些情况是可能发生的,哪些情况是不可能发生的。
2.光以60°的入射角从空气射入折射率n=\(\sqrt 3 \)的玻璃中,折射角是多大?画出光路图。
3.根据水和水晶的折射率,分别算出光在其中的传播速度。水中的光速大约是真空中的光速的几分之几?
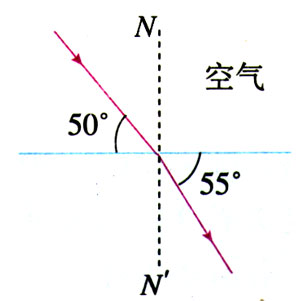
4.图13.1-6是光由空气射入某种介质时的折射情况,试由图中的数据求出这种介质的折射率和这种介质中的光速。
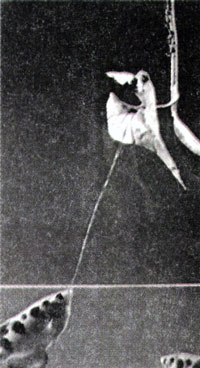
5.图13.1-7是射水鱼在水中准确射中水面上约1m远的小昆虫的照片。请你利用光的折射的知识分析,水中的鱼看到小昆虫的位置是在实际昆虫的上方还是下方?
6.关于图13.1-3测定玻璃折射率的实验,回答以下问题。
(1)证明图中的入射光线与射出玻璃砖的光线是平行的。
(2)如果光射入和射出玻璃的两个平面是平行的,射出玻璃砖的光线相对入射光线来说产生了侧移。证明:入射角越大侧移越大。
(3)为减小实验误差,入射角大一些好还是小一些好?
[1] 托马斯·杨(T.Young,1773~1829)。英国物理学家、考古学家、医生,光的波动说的奠基人之一。
发布时间:2017/1/18 下午9:22:21 阅读次数:9066
