两力合成

求两个力的合力，画出力的合成图。

解析

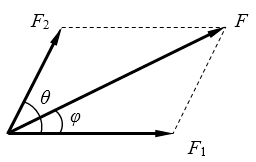
如图1所示，两个力F₁和F₂的合力大小为

F＝\(\sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \theta } \)

夹角为

φ＝arctan\(\frac{{{F_2}\sin \theta }}{{{F_1} + {F_2}\cos \theta }}\)

程序

main.m代码如下：

%两力的合成的主程序
clear                                  %清除变量
f1=30;                                 %第1个力
f2=50;                                 %第2个力
theta=60;                              %两力之间的夹角
P0_14fun(f1,f2,theta)                  %调用函数文件画力的合成图
P0_14fun(f1,60,120)                    %调用函数文件画力的合成图

fun.m代码如下。

%两力的合成的函数文件
function fun(f1,f2,theta)
th=theta*pi/180;                       %角度化为弧度
f=sqrt(f1^2+f2^2+2*f1*f2*cos(th));     %合力的大小
phi=atan2(f2*sin(th),f1+f2*cos(th));   %合力的方向
fx=[f1,f2*cos(th),f*cos(phi)];         %力的x分量
fy=[0,f2*sin(th),f*sin(phi)];          %力的y分量
figure                                 %创建图形窗口
quiver([0,0,0],[0,0,0],fx,fy,0,'LineWidth',2)%画力矢量
hold on                                %保持图像
plot([f1,fx(3)],[0,fy(3)],'--','LineWidth',2)%画斜虚线
plot([fx(2),fx(3)],[fy(2),fy(3)],'--','LineWidth',2)%画横虚线
axis equal                             %使坐标间隔相等
grid on                                %加网格
fs=16;                                 %字体大小
title('两力的合成','FontSize',fs)      %标题
xlabel('\itF_x\rm/N','FontSize',fs)    %标记横坐标
ylabel('\itF_y\rm/N','FontSize',fs)    %标记纵坐标
txt{1}=['\itF\rm_1=',num2str(f1),'N']; %第一个分力元胞
txt{2}=['\itF\rm_2=',num2str(f2),'N,\it\theta\rm=',...
    num2str(theta),'\circ'];           %第二个分力元胞
txt{3}=['\itF\rm=',num2str(f),'N'];    %合力元胞
text(fx,fy,txt,'FontSize',fs)          %标记力
phi(abs(phi)<1e-5)=0;                  %角度太小则作零处理
text(0,0,['\it\phi\rm=',num2str(phi*180/pi),'\circ'],'FontSize',fs)%标记角度
phi=linspace(0,phi);                   %角度向量
plot(f/10*cos(phi),f/10*sin(phi))      %画角度圆弧

说明

1．从键盘输入两个力的大小和角度，使程序灵活通用。

2．根据公式计算合力。

3．计算合力的角度时要用第2反正切函数，其值在－π到π之间。

4．箭杆指令quiver中第一个和第二个参数（三个零）分别表示三个箭杆的起点横坐标和纵坐标，第三个和第四个参数分别表示箭杆水平长度和竖直长度，第五个参数0表示不用自动刻度而用箭杆的规定长度。

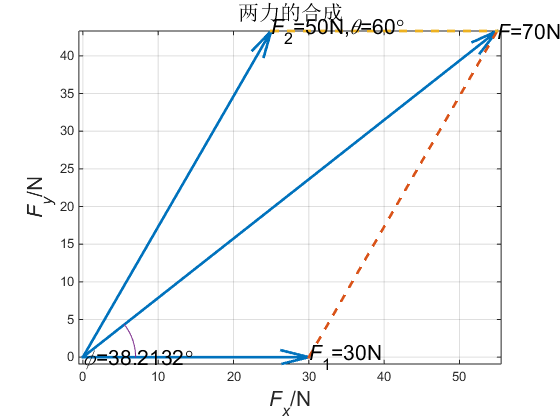
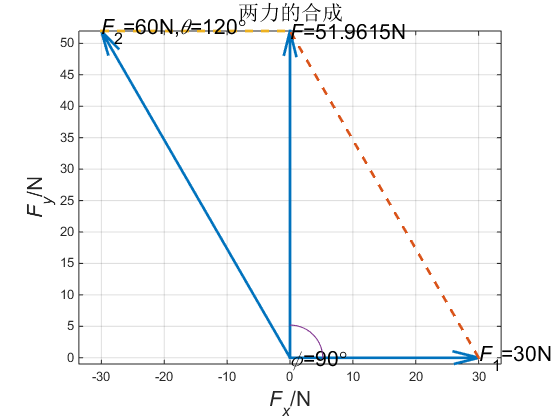
5．画虚线形成平行四边形。当F₁＝30N，F₂＝50N，θ＝60°时，力的合成如图2所示；当F₁＝30N，F₂＝60N，θ＝120°时，力的合成如图3所示。

6．将文本放在元胞中，用文本指令标记力的大小。

7．在图形窗口中往往要显示希腊字母或特殊字符。MATLAB作图所用的希腊字母如表1所示，MATLAB作图常用的字符为表2所示。

8．当初值或（和）终值是无理数时，常用linspace函数形成向量，以免漏掉初值或终值。

发布时间：2017/1/17 下午2:14:18  阅读次数：8693