第十二章 4 波的反射和折射

对着悬崖喊一声，过一小会儿就会听到回声，这是声波在悬崖上的反射。绳子的一端系在墙上，将另一端迅速上下抖动一次，可以看到凸起和凹下部分向墙的方向传播，在到达绳的固定端后又被反射回来。

演示

在水槽的一端放置振动发生器，它的窄条形平板能够周期性地打击水面，产生水波。可以看到，水波传播到挡板后被反射出去。图12.4-1中带箭头的直线表示波的传播方向。

为了解释与波的传播相关的现象，惠更斯提出了一个原理，不过在学习这个原理之前先要了解几个概念。

波面和波线

假设水面O点有一个波源，水波向四周传开。由于向各个方向的波速都一样，所以向四面八方传播的波峰组成了一个个圆，波谷也组成了一个个圆；实际上，任何振动状态相同的点都组成了一个个圆。我们把这些圆叫做一个个波阵面或波面（图12.4-2），而与波面垂直的那些线代表了波的传播方向，叫做波线。

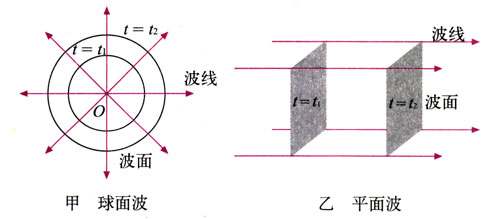
当然，在水波的例子中，波面还不是面，因为水波只在水面传播。可以想像，对于空间一点发出的球面波，它的波阵面就是以波源为球心的一个个球面，而波线就是这些球面的半径。如果波面是平面，它就是平面波（图12.4-2乙）。当然，如果在纸上画出来，平面波的波面只是一条直线。

惠更斯原理

惠更斯在1690年提出：介质中任一波面上的各点，都可以看做发射子波的波源，其后任意时刻，这些子波在波前进方向的包络面就是新的波面。这就是常说的惠更斯原理（Huygens principle）。

如果知道某时刻一列波的某个波面的位置，还知道波速，利用惠更斯原理可以得到下一时刻这个波面的位置，从而确定波的传播方向。下面以球面波为例做些说明。

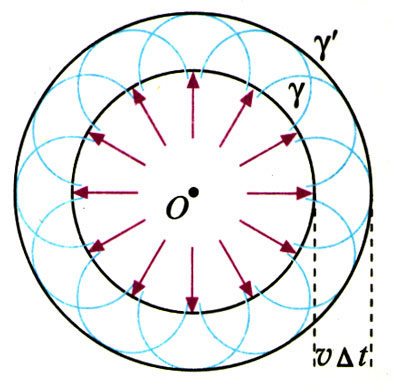
如图12.4-3，以O为球心的球面波在时刻t的波面为γ，按照惠更斯原理，γ面上每个点都是子波的波源。在Δt时间之后各子波的波面如图中浅色线所示。假设波在同种均匀介质中传播，波向各个方向传播的速度都相等，所以浅色线圆的半径vΔt也都相等。γʹ是这些子波波面的包络面，它就是原来球面波的波面γ在时间Δt后的新位置。可以看出，新的波面仍是一个球面，它与原来球面的半径之差为vΔt，表示波向前传播了vΔt的距离。这个结论与常识一致。

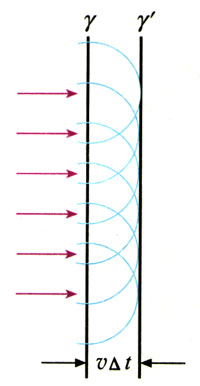
与此类似，可以用惠更斯原理说明平面波的传播（图12.4-4）。

波的反射

用惠更斯原理不但可以说明为什么波在两种介质的界画会发生反射，而且可以得到反射角与入射角的关系。

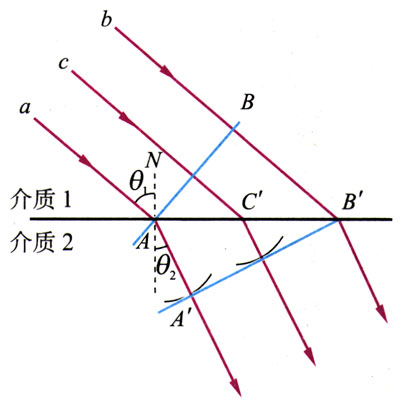
如图12.4-5，一列平面波到达两种介质的界面，AB是这列波的一个波面。由于入射波的传播方向与界面并不垂直，a、c、b三条波线并不同时到达界面，它们到达界面时产生子波的时间也就有先有后，子波传播的距离也就有远有近。当波面上的B点刚刚到达界面上的Bʹ点时，A、Cʹ两点发出的子波的波面如图中两小段圆弧所示，它们的包络面为图中的AʹBʹ，这是反射后新的波面，aʹ、cʹ、bʹ三条射线与波面AʹBʹ垂直，是反射波的波线，代表了反射波的传播方向。

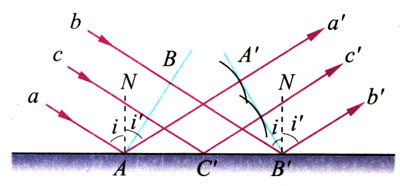
下面推导反射角与入射角的关系。

在直角三角形ABʹB与直角三角形BʹAAʹ中，ABʹ是公共边；波从B传播到Bʹ所用的时间与子波从A传播到Aʹ所用的时间是一样的，而波在同种介质中的波速不变，所以BʹB＝AAʹ。

因此

直角三角形ABʹB≌直角三角形BʹAAʹ

所以

∠AʹABʹ＝∠BBʹA

从图12.4-5看出，入射角i和反射角iʹ分别为∠BBʹA和∠AʹABʹ的余角，所以

iʹ＝i

也就是说，在波的反射中，反射角等于入射角。

波的折射

当波由一种介质进入另一种介质时会发生什么现象？我们尝试用惠更斯原理做出预言。

如图12.4-6，一束平面波中的波线a首先于时刻t由介质1到达界面。波线a进入介质2后，又经过时间Δt，波线b也到达界面。这时A、Cʹ两点发出的子波的波面如图中两小段圆弧所示，它们的包络面为图中的AʹBʹ，这是波进入介质2之后的新的波面。由于是两种不同的介质，其中波的传播速度v₁，v₂不一定相同，在Δt这段时间内，两条波线a和b前进的距离AAʹ和BBʹ也不一定相同。因此波进入第二种介质后传播方向常常发生偏折。

在初中学习光学时已经知道了入射角和反射角的概念。类似地，我们把入射时波线与法线的夹角叫做入射角，反射时波线与法线的夹角叫做反射角。

波在第1种介质中的传播方向（波线的方向）与法线间的夹角称为入射角（incident angle），如图12.4-6中的θ₁；波进入第2种介质后，它的传播方向（波线的方向）与法线间的夹角称为折射角（refraction angle），如图12.4-6中的θ₂。利用平面几何的知识可以得到折射角θ₂与入射角θ₁的以下关系

\(\frac{{\sin {\theta _1}}}{{\sin {\theta _2}}}\)＝\(\frac{{{v_1}}}{{{v_2}}}\)                         （1）

如果有兴趣，可以试着证明（1）式。

由于一定介质中的波速是一定的，所以\(\frac{{{v_1}}}{{{v_2}}}\) 是一个只与两种介质的性质有关而与入射角度无关的常数，叫做第2种介质对第1种介质的折射率（refractive index），以n₁₂表示[1]

n₁₂＝\(\frac{{{v_1}}}{{{v_2}}}\)                        （2）

从（1）式可以看出，如果第2种介质中的波速小于第一种介质中的波速，波在进入第2种介质后，传播方向将向法线靠拢。这个结论与实验得到的波的折射定律（refraction law）是一致的。

做一做

观察水波的折射

在水槽中放入一块厚度均匀的玻璃板，注意使它的一条边不与波传来的方向垂直，如图12.4-7中虚线a所示的位置。然后加水，使水面高过玻璃板。接通电源产生水波，观察水波经过水深不同的区域时传播方向的变化。

通过这个实验，你认为水槽中水波的波速与水的深浅有什么关系？

海边的波涛，为什么总是沿着与海岸垂直的方向袭来？

科学漫步

回声、混响和建筑声学

各种波在传播过程中如果遇到大的障碍物，都会发生反射，声波也是一样。同学们都有这样的经验，在山谷中大喊一声，过一会儿能够听到回声。知道了声速就可以根据回声到来的时间测出人与山的距离。打雷时听到的隆隆声可以持续很久，原因之一就是声波在地面、云层以及山谷之间发生了多次反射。

声波遇到普通房间的墙壁、地面、天花板也会反射，但是由于回声与原声几乎同时到达，而入耳只能分辨相差0.1 s以上的两个声音，所以在房间里不能听到回声，但会感到声音比在野外时大些。由于墙壁、地面、天花板对声波的多次反射，当声源停止发声后，声音要经过一段时间才会消失，这种现象叫做混响，这段时间叫做混响时间。混响时间的长短是音乐厅、剧院、礼堂等建筑物的重要声学特性。对讲演厅来说，混响时间不能太长。我们平时讲话，每秒大约发出2至3个音节，如果混响时间太长，发出下波一个音节的时候上一个音节的声音还很强，那就不容易听清楚。混响时间也不能太短，太短了听起来就像在旷野里说话，同样听不清。北京科学会堂有一个会议厅，坐满人时实测的混响时间是1s。

音乐厅的最佳混响时间要比会议厅长些，不过也不完全一样。上演轻音乐时，混响时间要短些，这样能使节奏更为鲜明；交响乐的混响时间可以长些，这样听起来更加混厚有力。北京的首都剧场，坐满观众时的混响时间是1.36 s，空的时候是3.3 s，这是因为满座时人的衣服、皮肤等吸声表面增大，所以混响时间缩短。

高级的音乐厅或剧场，为了不同的要求，需要人工调节混响时间。其中一种办法是改变厅堂的吸声情况。在大厅墙壁上嵌入一组可以转动的圆柱体，柱面的一半是反射面，另一半是吸声面。把反射面转到厅堂内部，混响时间增加；把吸声面转到厅堂内部，混响时间变短。有的剧场坐椅的下表面也是软的，没人坐的时候椅面翻起，软面朝向舞台，能够增加吸声的表面，这样可以避免观众较少时混响时间过长。

高水平的音乐会都不使用扩音设备，目的是使观众直接听到舞台上的声音，完整地体会演员表达的情感。为了让全场观众都能清楚地听到较强的声音，音乐厅的天花板上挂着许多反射板。这些反射板的大小、角度和安放位置都经过精确设计，能把舞台上的声音反射到大厅的各个角落。

处理各种建筑物的声学特性，取得好的声音效果，这门学问叫做建筑声学。

问题与练习

1．一个人在高处用望远镜看到，远处地面的木工以每秒一次的频率钉钉子。他听到声音时恰好看到锤子打在钉子上。木工停止敲击后，他还听到一次敲击声。木工离他有多远？

2．一列声波在空气中的波长为25 cm，传播速度为340 m/s。这列声波传入另一介质中时，波长变为80 cm，它在这种介质中的传播速度是多少？

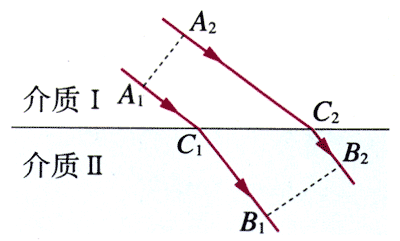
3．如图12.4-9，一列平面波朝着两种介质的界面传播，A₁A₂是它在介质Ⅰ中的一个波面，A₁C₁和A₂C₂是它的两条波线，其入射角为53°（sin53°取0.8）。C₁和C₂位于两种介质的界面上。B₁B₂是这列平面波进入介质Ⅱ后的一个波面。已知A₁A₂的长度为0.6 m，介质Ⅰ和介质Ⅱ中的波速之比为4∶3，问：A₁C₁B₁与A₂C₂B₂的长度相差多少？

发布时间：2017/1/12 上午7:39:25  阅读次数：3225