第十二章 3 波长、频率和波速

我们以横波为例讨论波长。

在图12.1-3中，从t＝0到t＝T这段时间里，由质点P₀发出的振动传到质点P₈，使质点P₈开始振动。这时质点P₀恰好结束了一次全振动而开始下一次全振动，因而质点P₀和质点P₈的振动步调完全一致。也就是说，这两个质点振动的相位相同，它们在任何时刻对平衡位置的位移的大小和方向总是相等的。同样，质点P₁和P₉、P₂和P₁₀…它们每一对在振动中的相位也总是相同的。

在波动中，振动相位总是相同的两个相邻质点间的距离，叫做波长（wavelength），通常用λ表示（图12.3-1）。

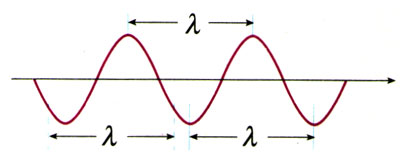
在横波中，两个相邻波峰或两个相邻波谷之间的距离等于波长。在纵波中，两个相邻密部或两个相邻疏部之间的距离等于波长。

在波动中，各个质点的振动周期或频率是相同的，它们都等于波源的振动周期或频率，这个周期或频率也叫做波的周期或频率。在图12.1-3中，由质点P₀发出的振动，经过一个周期传到质点P₈，也就是说，经过一个周期T，振动在介质中传播的距离等于一个波长λ，所以机械波在介质中传播的速度为

v＝\(\frac{\lambda }{T}\)                                                      （1）

由于周期T与频率f互为倒数，即f＝\(\frac{1}{T}\)，所以上式也可以写成

v＝fλ                                                        （2）

（1）、（2）两式的关系虽然是从机械波得到的，但是它对于以后要学习的电磁波也适用。

机械波在介质中的传播速度由介质本身的性质决定，在不同的介质中，波速是不同的。下表列出了0℃时声波在几种介质中的传播速度。声速还与温度有关，如20℃时空气中的声速为344 m/s，比0℃时略大些。

游泳时耳朵在水中听到的音乐与在岸上听到的是一样的，说明机械波从一种介质进入另一种介质，频率并不改变；但由于波速变了，所以波长会改变。

例题1

某乐律C调“la”的频率为f＝440 Hz，试求这个乐音在空气中的波长和在水中的波长。

解   根据波速、频率、波长的关系v＝f λ，可以求出波长

λ＝\(\frac{\lambda }{f}\)

水中的声速为1 450 m/s，空气中的声速为332 m/s（设温度为0℃），把两个值分别代入上式，得到

λ_水＝\(\frac{\lambda_水 }{T_水}\) ＝\(\frac{1450}{440}\) m＝3.3 m

λ_气＝\(\frac{\lambda_气 }{T_气}\) ＝\(\frac{332}{440}\) m＝0.75 m

通过这个例子可以看出，频率一定的声音，在不同的介质中的波长是不同的。

例题2

图12.3-2中的实线是一列正弦波在某一时刻的波形曲线。经0.5 s后，其波形如图中虚线所示。设该波的周期T大于0.5 s。

（1）如果波是向左传播的，波的速度是多大？波的周期是多大？

（2）如果波是向右传播的，波的速度是多大？波的周期是多大？

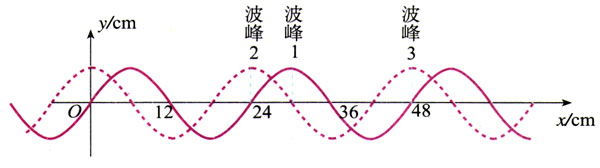
分析       根据题意，这列波的周期大于0.5 s，所以经过0.5 s的时间，这列波传播的距离不可能大于一个波长λ。当波向左传播时，图中的波峰1只能到达波峰2，而不可能向左到达更远的波峰。当波向右传播时，图中的波峰1又能到达波峰3，而不可能向右到达更远的波峰。

已知波传播的时间为t＝0.5 s，由图可以知道波的传播距离Δx，由公式v＝\(\frac{{\Delta x}}{t}\)就能够求出波的传播速度v。

又，由图可以知道波长λ，由公式v＝\(\frac{\lambda }{T}\)就能够求出周期T。

解（1）如果波是向左传播的，从图12.3-2看出，虚线所示的波形相当于实线所示的波形向左移动了6 cm（\(\frac{1}{4}\)个波长），由此可求出波速的大小

v＝\(\frac{{\Delta x}}{t}\)＝\(\frac{0.06}{0.5}\)m/s＝0.12 m/s

波的周期为

T＝\(\frac{\lambda }{v}\)＝ \(\frac{0.24}{0.12}\)s＝2.0 s

（2）如果波是向右传播的，从图12.3-2看出，虚线所示的波形相当于实线所示的波形向右移动了18 cm（\(\frac{3}{4}\)个波长），由此可以求出波速的大小

v＝\(\frac{{\Delta x}}{t}\)＝\(\frac{0.18}{0.5}\)m/s＝0.36 m/s

波的周期为

T＝\(\frac{\lambda }{v}\)＝\(\frac{0.24}{0.36}\)s＝0.67 s

问题与练习

1．一个高个子人和一个矮个子人并肩行走（图12.3-3），哪个人的双腿前后交替更为频繁？如果拿这两个人与两列波做类比，波长、频率、波速分别可以比做什么？

2．据你所知，人能听到的声音的最低频率和最高频率大致各是多少？你知道自己能听到的声音的最高频率吗？你认为可以用什么方法来测定？

3．海面上停着一条船，一个人观察到每隔10 s有一个波峰经过这条船，他还注意到相邻波峰间的距离大约是150 m。试由这些数据估算海面波浪的速度。

4．湖面上停着A、B两条小船，它们相距20 m。一列水波正在湖面上传播，每条小船每分钟上下浮动20次。当A船位于波峰时，B船在波谷，两船之间还有一个波峰。求水波的波速。

5．第一次测定声音在水中的传播速度是1827年在日内瓦湖上进行的（图12.3-4）：两条船相距14 km，实验员在一条船上敲响水里的一口钟，同时点燃船上的火药使其发光；另一条船上的实验员在看到火药发光后10 s，通过水里的听音器听到了水下的钟声。试根据这些数据计算水中的声速。

发布时间：2017/1/11 上午11:44:36  阅读次数：7954