第十一章 5 外力作用下的振动
做简谐运动的物体受到的回复力,是振动系统内部的相互作用力。如果振动系统不受外力的作用,此时的振动叫做固有振动,其振动频率称为固有频率(natural frequency)。倘若振动系统受到外力作用,它将如何运动?
阻尼振动
振动系统最常见的外力是摩擦力或其他阻力。当系统受到阻力的作用时,我们说振动受到了阻尼。系统克服阻尼的作用要做功,消耗机械能,因而振幅减小,最后停下来。这种振幅逐渐减小的振动,叫做阻尼振动(damped vibration)。图动11.5-1是阻尼振动的图象。
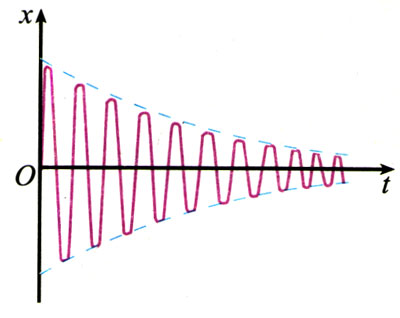
振动系统受到的阻尼越大,振幅减小得越快。阻尼过大时,系统不能发生振动。阻尼越小,振幅减小得越慢,当阻尼很小时,在不太长的时间内看不出振幅有明显的减小,于是可以把它当做简谐运动来处理。前面关于简谐运动的演示就属于这种情形。
设想弹簧振子浸在泥浆中,把小球拉开再放开,它只能缓慢地回到平衡位置,而不能振动。
受迫振动
阻尼振动最终要停下来,那么怎样才能产生持续的振动呢?最简单的办法是使周期性的外力作用于振动系统,外力对系统做功,补偿系统的能量损耗,使系统的振动维持下去。这种周期性的外力叫做驱动力,系统在驱动力作用下的振动叫做受迫振动(forced vibration)。机器运转时底座发生的振动、扬声器纸盆的振动,都是受迫振动。
受迫振动的频率与什么因素有关呢?
演示
如图11.5-2,架子上面的电动机向弹簧一小球系统施加周期性的驱动力,使小球做受迫振动。改变电动机的转速可以调整驱动力的频率。
接通电源,使小球做受迫振动,记录驱动力的周期和小球振动的周期。改变驱动力的周期(频率),再做记录。小球做受迫振动的周期(频率)与驱动力的周期(频率)有什么关系?

共振
通过以上研究我们知道,不管系统的固有频率如何,它做受迫振动的频率总等于驱动力的频率,与系统的固有频率无关。但是,在一定驱动力作用下的受迫振动,其振幅是否也跟它的固有频率无关呢?
实验
如图11.5-3,在一条张紧的绳子上挂几个摆,其中A、B的摆长相等。当A摆振动的时候,通过张紧的绳子给其他各摆施加驱动力,使其余各摆做受迫振动。驱动力的频率等于A摆的频率。其他各摆的固有频率取决于自己的摆长。
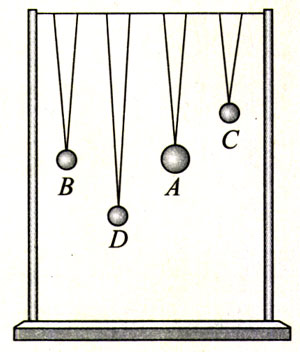
B、C、D三个摆在驱动力的作用下开始摆动,观察它们振幅的差别。三个摆的振幅与它们的固有频率有什么关系?
实验表明,当系统做受迫振动时,如果驱动力的频率十分接近系统的固有频率,系统的振幅会很大。
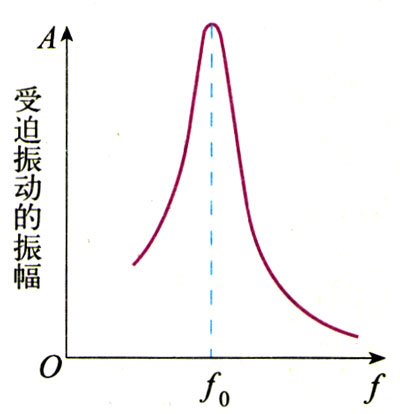
如果驱动力的频率可以调节,把不同频率的驱动力先后作用于同一个振动系统,其受迫振动的振幅将不同。图11.5-4的曲线表示某振动系统的受迫振动的振幅A随驱动力频率f变化的关系。可以看出:驱动力频率f等于系统的固有频率f0时,受迫振动的振幅最大,这种现象叫做共振[1](resonance)。
科学漫步
我国古代对共振早有了解。据《天中记》一书记载,晋初(公元3世纪)时,京城有户人家挂着的铜盘每天早晚轻轻自鸣两次,人们十分惊恐。学者张华判断,这是铜盘与皇宫早晚的钟声共鸣所致。后来把铜盘磨薄一些(改变固有频率),它就不再自鸣了。我国古代乐器的研制,也反映了当时人们对共振的认识。
共振在现代生活中有着许多应用。一些不同长度的钢片安装在同一个支架上,可以制作转速计。把这样的转速计与开动着的机器紧密接触,机器的振动引起转速计的轻微振动,这时固有频率与机器转速一致的那个钢片发生共振,振幅最大。读出这个钢片的固有频率,就知道机器的转速。
共振筛是利用共振现象制成的。把筛子用四根弹簧支起来,在筛架上安装一个偏心轮,就成了共振筛。偏心轮在发动机的带动下转动时,适当调节偏心轮的转速,可以使筛子受到的驱动力的频率接近筛子的固有频率,筛子发生共振,提高了筛选工作的效率。
在某些情况下,共振可能造成损害。军队或火车过桥时,整齐的步伐或车轮对铁轨接头的撞击会对桥梁产生周期性的驱动力,如果驱动力的频率接近桥梁的固有频率,就可能使桥梁的振幅显著增大,致使桥梁断裂。因此,部队过桥要便步走,以免产生周期性的驱动力,火车过桥要慢速,使驱动力的频率远小于桥梁的固有频率。

轮船航行时,如果所受波浪冲击力的频率接近轮船左右摇摆的固有频率,轮船可能倾覆。这时应该改变航向,使波浪冲击力的方向与轮船摇摆的方向不一致,同时要改变航速,使波浪冲击的频率远离轮船摇摆的固有频率。
机器运转时,零部件的运动,如活塞的运动、轮的转动,会产生周期性的驱动力。如果驱动力的频率接近机器本身或支持物的固有频率,就会发生共振,使机器或支持物损坏。这时要采取措施,如调节机器的转速,使驱动力的频率与机器或支持物的固有频率不一致。同样,厂房建筑物的固有频率也不能处在机器转动的频率范围之内。
除了避免共振之外,有时我们还需要减振,以降低外界冲击力对物体的破坏作用。减振的思路之一是给被保护的物体加一层减振的阻尼材料,使冲击过程的机械能尽量多地转化为阻尼材料的内能,减轻被保护物受到的冲击作用。例如,用泡沫塑料作为商品的内包装,就能起到这种作用。
减振的另一个思路悬在物体与外界冲击作用之间安装一个“质量—弹簧”系统。对一个周期性变化的驱动力来说,在一段较长时间(远大于1周期)内,其驱动力的平均值是非常小的。外界冲击力作用在一个质量—弹簧系统上时,如果该系统的固有周期比外界冲击力的周期大很多,它不会及时地把冲击力传递给物体,这种延缓的过程实际上对冲击力起到了“平均”的作用。图11.5-6是汽车三级减振的示意图,最下面的是由车轮的轴和轮胎组成的第一级质量一弹簧系统,车身和底座弹簧构成第二级,乘客和座椅弹簧构成第三级,这些质量一弹簧系统的固有频率都比较低,能对来自地面的频率较高的振动起到很好的减振作用。

问题与练习
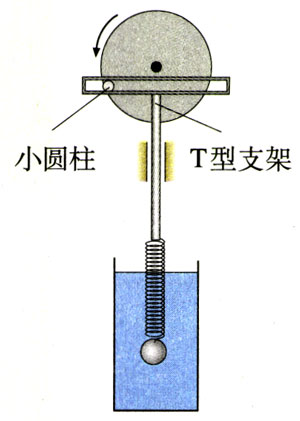
1.如图11.5-7所示,一个竖直圆盘转动时,固定在圆盘上的小圆柱带动一个T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球组成的振动系统,小球浸没在水中。当圆盘静止时,让小球在水中振动,其阻尼振动的频率约为3 Hz。现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定,它振动的频率是多少?
2.如图11.5 -8所示,张紧的水平绳上吊着A、B、C三个小球。B靠近A,但两者的悬线长度不同;C远离球A,但两者的悬线长度相同。
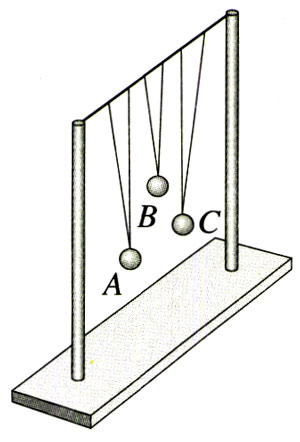
(1)让球A在垂直于水平绳的方向摆动,将会看到B、C球有何表现?
(2)在C球摆动起来后,用手使A、B球静止,然后松手,又将看到A、B球有何表现?
3.汽车的车身是装在弹簧上的,某车的车身一弹簧系统的固有周期是1.5 s。这辆汽车在一条起伏不平的路上行驶,路面凸起之处大约都相隔8m。汽车以多大速度行驶时,车身上下颠簸得最剧烈?
4.图11.5-9是一个单摆的共振曲线。
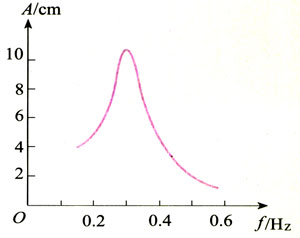
(1)试估计此单摆的摆长。
(2)若摆长增大,共振曲线的最大值将怎样移动?
[1] 对于有阻尼的真实振动,当驱动力的频率略小于固有频率时,系统的振幅达到最大值,阻尼越大,这两个频率的差别越明显。
发布时间:2017/1/8 下午1:21:51 阅读次数:5304
