第十一章 3 简谐运动的回复力和能量
我们已经学过,物体做匀变速运动时,所受的合力大小、方向都不变;物体做匀速圆周运动时,所受的合力大小不变、方向与速度方向垂直并指向圆心。那么,物体做简谐运动时,所受的合力有什么特点?
前两节只研究做简谐运动的质点的运动的特点,不涉及它所受的力,是从运动学的角度研究的。本节要讨论它所受的力,是从动力学的角度研究的。
简谐运动的回复力
如图11.3-1,在弹簧振子的例子中,小球所受的力F与弹簧的伸长量成正比。由于坐标原点就是平衡位置,弹簧的伸长量与小球位移x的大小相等,因此有
F=-kx (1)
式中k是弹簧的劲度系数。因为当x在原点的左侧,即x取负值时,力F沿坐标轴的正方向;而x在原点右侧,取正值时,力F沿坐标轴的负方向,所以式中有负号。
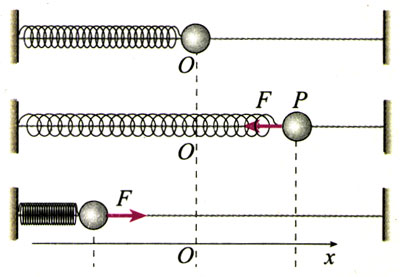
理论上可以证明,如果质点所受的力具有(1)式的形式,也就是说:如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动。由于力的方向总是指向平衡位置,它的作用总是要把物体拉回到平衡位置,所以通常把这个力称为回复力(restoring force)。
简谐运动的能量
弹簧振子的速度在不断变化,因而它的动能在不断变化;弹簧的伸长量或压缩量在不断变化,因而它的势能也在不断变化。它们的变化具有什么规律?
思考与讨论
作为一个振动系统,弹簧振子的势能与弹簧的伸长量有关,动能与小球的速度有关。请在下表中填出图11.3-2中的弹簧振子在各位置的能量。某量取最大值、最小值用文字表示,某量为零用数字0表示,增加和减少分别用斜向上的箭头和斜向下的箭头表示。
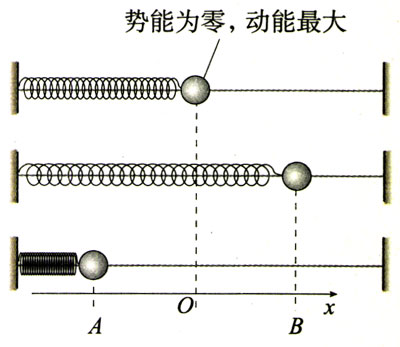
|
位置 |
A |
A→O |
O |
O→B |
B |
|
位移的大小 |
|
|
|
|
|
|
速度的大小 |
|
|
|
|
|
|
动能 |
|
|
|
|
|
|
势能 |
|
|
|
|
|
|
总能 |
|
|
|
|
|
理论上可以证明,如果摩擦等阻力造成的损耗可以忽略,在弹簧振子运动的任意位置,系统的动能与势能之和都是一定的,这与机械能守恒定律相一致。
实际的运动都有一定的能量损耗,所以简谐运动是一种理想化的模型。
做一做
弹簧下面悬挂的钢球,它所受的力与位移之间的关系也具有(1)式的形式吗?由于平衡时弹簧已经有了一个静伸长量h,问题稍稍麻烦一点。这时仍要选择钢球静止时的位置为坐标原点,而小球所受的回复力实际上是弹簧的弹力与重力的合力。
请你试着导出小球所受的合力与它的位移的关系。
问题与练习
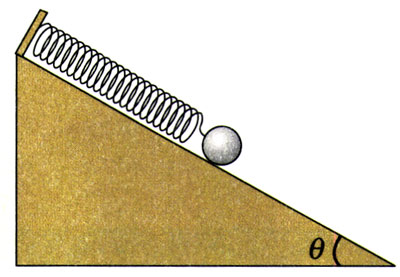
1.一个振动,如果回复力与偏离平衡位置的位移成正比且方向与位移相反,就能判定它是简谐运动。请你据此证明:把图11.3-3中倾角为θ的光滑斜面上的小球沿斜面拉下一段距离,然后松开,小球的运动是简谐运动。
2.某人想判定以下振动是不是简谐运动,请你陈述求证的思路(可以不做定量证明):
(1)粗细均匀的一条木筷,下端绕几圈铁丝,竖直浮在较大的筒中(图11.3-4)。把木筷往上提起一段距离后放手,木筷就在水中上下振动;

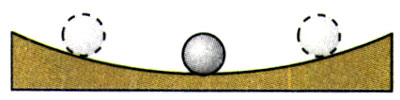
(2)光滑圆弧面上有一个小球,把它从最低点移开一小段距离,放手后,小球以最低点为平衡位置左右振动(图11.3 -5)。
3.做简谐运动的物体经过A点时,加速度的大小是2 m/s2,方向指向B点;当它经过B点时,加速度的大小是3 m/s2,方向指向A点。若AB之间的距离是10 cm,请确定它的平衡位置。
4.图11.3-6为某物体做简谐运动的图象,在所画曲线的范围内回答下列问题。
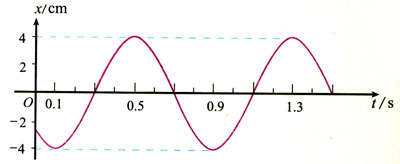
(1)哪些时刻物体的回复力与0.4 s时刻的回复力相同?
(2)哪些时刻物体的速度与0.4 s时刻的速度相同?
(3)哪些时刻的动能与0.4 s时刻的动能相同?
(4)哪些时间的加速度在减小?
(5)哪些时间的势能在增大?
文件下载(已下载 316 次)发布时间:2017/1/5 上午7:31:07 阅读次数:3118
