第十一章 2 简谐振动的描述

描述简谐运动的物理量

我们以弹簧振子为例来研究描述简谐运动的物理量。

振幅

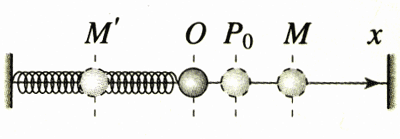
如图11.2-1，振子在水平杆上的M点和Mʹ点之间往复振动，O为它的平衡位置。图中OM＝OMʹ，，它们是振动物体离开平衡位置的最大距离，叫做振动的振幅（amplitude）。振幅的两倍表示的是做振动的物体运动范围的大小。

周期和频率

简谐运动是一种周期性运动。图11.2-1中，如果从振子向右通过O点的时刻开始计时，它将运动到M，然后向左回到O，又继续向左运动到达Mʹ，之后又向右回到O。这样一个完整的振动过程称为一次全振动。不管以哪里作为开始研究的起点，例如从图中的P₀开始运动，弹簧振子完成一次全振动的时间总是相同的。

做简谐运动的物体完成一次全振动所需要的时间，叫做振动的周期（period），单位时间内完成全振动的次数，叫做振动的频率（frequency）。周期和频率都是表示物体振动快慢的物理量，周期越小，频率越大，表示振动越快。用T表示周期，用f表示频率，则有

f＝\(\frac{1}{T}\)                                                                （1）

在国际单位制中，周期的单位是秒。频率的单位是赫兹（hertz），简称赫，符号是Hz。1 Hz＝1 s^-1。

我们用周期和频率描述简谐运动，实际上，描述任何周期性过程时，即使不是简谐运动，也要用到这两个概念。它们的应用范围已经扩展到物理学以外的领域了。

做一做

如图11.2-2，弹簧上端固定，下端悬吊钢球。把钢球从平衡位置向下拉下一段距离A，放手让其运动，A就是振动的振幅。用秒表测出钢球完成n个全振动所用的时间t，\(\frac{t}{n}\)就是振动的周期。n的值取大一些可以减小周期的测量误差。

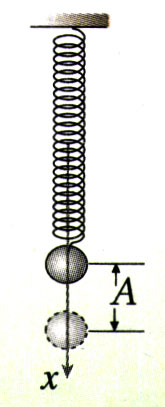
再把振幅减小为原来的一半，用同样的方法测量振动的周期。

通过这个实验你有什么发现？由此你对简谐运动的周期与振幅的关系有什么猜想？

相位

除了振幅、周期和频率外，要完整地描述简谐运动以及任何周期性运动，还需要另一个物理量。

实验

有并列悬挂的两个小球，悬线的长度相同。把它们拉起同样的角度后同时放开。可以看到，它们的振幅、周期（频率）也都相同。

但是如果先把第一个小球放开，然后再放第二个，这种情况下尽管两个小球运动的振幅和周期还都是相同的，但它们运动的步调不再一致了。例如，当第一个小球到达平衡位置时再放开第二个，那么当第一个到达另一方的最高点时，第二个刚刚到达平衡位置；而当第二个到达另一方的最高点时，第一个小球已经返回平衡位置了。与第一个小球相比，第二个总是滞后\(\frac{1}{4}\)个周期，或者说总是滞后\(\frac{1}{4}\)个全振动。

在物理学中，我们用不同的相位（phase）来描述周期性运动在各个时刻所处的不同状态。例如，对于同时放开的两个小球，我们说它们的相位相同，而对于上面说的不同时放开的两个小球，我们说第二个小球的相位落后于第一个的相位。

科学漫步

月相

描述自然界的许多周期性变化都会用到相位的概念。例如，从地球上看，月亮从圆到缺，又从缺到圆，这是一种周期性的变化（图11.2-3）周期为29.5天。月亮的这种圆缺变化叫做月相变化。为了便于记忆，人们还给几个特殊的月相起了特殊的名称：

望——满月

下弦——恰好有半个月面是亮的

朔——这时实际上看不见月亮

上弦——恰好另半个月面是亮的

在望和下弦之间的“月芽”称为残月；在朔和上弦之间的“月芽”称为新月。

你是否注意观察过，上弦时月面的弧线是在月面的东侧还是在西侧？上弦月出现在黄昏还是出现在黎明？

简谐运动的表达式

在数学课中，我们已经学习了正弦函数y＝Asin（ωx＋φ）的图象。在上节我们已经得知，正弦函数可以描述简谐运动，那么用位移x表示函数值，用时间t表示自变量，这个正弦函数式便写为

x＝A sin（ωt＋φ）                                                 （2）

因此，要描述简谐运动的位移x与时间t之间的定量关系，必须知道物理量A、ω、φ。它们是描述简谐运动的基本的物理量。

哪个量代表简谐运动的振幅？

因为| sin（ωt＋φ）|≤1，所以|x|≤A，也就是说，位移大小的最大值是A，所以（2）式中的A代表了图11.2-1中的OM，A代表简谐运动的振幅。

哪个量代表简谐运动的频率？

在数学课上我们已经知道，对于sin（ωt＋φ）来说，（ωt＋φ）这个量在从0增加到2π的过程中，sin（ωt＋φ）的值先从0增加到极大值1，又从极大值1经过0减小到极小值-1，然后又回到0，这样循环变化一次。现在的问题是，时间t每增加多少，sin（ωt＋φ）这个量循环变化一次？

设时间从t₁增加到t₂的过程中sin（ωt＋φ）循环一次，即周期为

T＝t₂－t₁

于是有

（ωt₂＋φ）－（ωt₁＋φ）＝2π

由此解出

ω＝\(\frac{{2\pi }}{T}\)

把（1）式代入，得

ω＝2πf                                                     （3）

可见，（2）式中的ω是一个与频率成正比的量，叫做简谐运动的“圆频率”。它也表示简谐运动的快慢。

哪个量代表简谐运动的相位？

数学课中我们已经学过，当（ωt＋φ）确定时，sin（ωt＋φ）的值也就确定了。所以（ωt＋φ）代表了做简谐运动的质点此时正处于一个运动周期中的哪个状态，可见（ωt＋φ）代表简谐运动的相位。φ是t＝0时的相位，称做初相位，或初相。

实际上经常用到的，是两个具有相同频率的简谐运动的相位差（phase difference），如果两个简谐运动的频率相等，其初相分别是φ₁和φ₂，当（φ₂＞φ₁时，它们的相位差是

∆φ＝（ωt＋φ₂）－（ωt＋φ₁）＝φ₂－φ₁

此时我们常说2的相位比1超前∆φ，或者说1的相位比2落后∆φ。

综上所述，做简谐运动的质点在任意时刻t的位移是

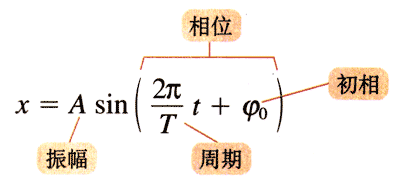
思考与讨论

表达式ωt＋φ看，相位的单位应该是怎样的？

科学漫步

乐音和音阶

在音乐理论中，把一组音按音调高低的次序排列起来就成为音阶，也就是大家都知道的do，re，mi，fa，sol，la．si，do（简谱记做“1”、“2”、“3”、“4”、“5”、“6”、“7”、“\(\dot 1\)”）。下表列出了某乐律C调音阶中各音的频率[1]。

有趣的是，高音do的频率正好是中音do频率的2倍，而且音阶中各音的频率与do的频率之比都是整数之比。

还有更有趣的事情。喜欢音乐的同学都知道，有些音一起演奏时听起来好听，有些音一起演奏时听起来不好听；前者叫做谐和音，后者叫做不谐和音。著名的大三和弦do、mi、sol的频率比是4∶5∶6；而小三和弦re、fa、la的频率比是10∶12∶15。大三和弦听起来更为和谐，那是因为三个音的频率比是更小的整数之比。随便拼凑在一起的三个音听起来不和谐，有兴趣的同学可以算一算它们的频率比，一定是三个大得惊人的整数。

从这个例子可以看到艺术后面的科学道理，但是，艺术远比1＋1＝2复杂。从上表中看出，频率增加一倍，音程高出8度。实际上这只对于中等音高是正确的。人的感觉十分复杂，对于高音段来说，频率要增加一倍多，听起来音高才高出一个8度。如果一个书呆子调琴师按照“频率翻倍”的办法调钢琴，那就要砸饭碗了。

尽管如此，科学家们还是可以通过音乐家的实际测听，确定音高与频率的对应关系，并且据此设计出优美动听的电子乐器。

做一做

用计算机观察声音的波形

绝大多数计算机的操作系统都有录音、放音的功能，并能在放音时显示声振动的图象。

用计算机的录音功能录制两个乐音，例如笛声，一个是do，另一个是sol，把它们保存起来。用媒体播放软件复现这个声音，并把播放软件界面中“条形与波浪”的选项设为“波形”。这样可以从电脑屏幕上看到播放声音时的振动图象。按下“暂停”键得到静止图象。

把do和sol这两个声音的振动图象复制到同一张空白幻灯片上，并把图象以外多余的区域剪裁掉，就得到图11.2-4所示的图形。在屏幕上作出矩形框，调节框的宽度，使框内包含“do”的10个周期。在屏幕上观察，多少个“sol”的周期与“do”的10个周期的时间相等？由此可以得到“sol”和“do”的频率之比。

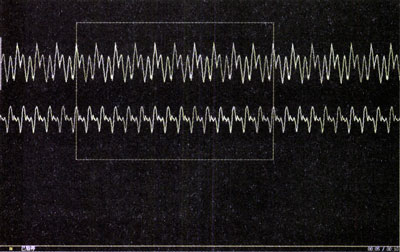
采用这种方法可以比较两个声音的频率之比。如果已知其中一个声音的频率，还可以推知另一个声音的频率。

问题与练习

1．有两个简谐运动：x₁＝3asin（4πbt＋\(\frac{\pi }{4}\)）和x₂＝9asin（8πbt＋\(\frac{\pi }{2}\)），它们的振幅之比是多少？它们的频率各是多少？t＝0时它们的相位差是多少？

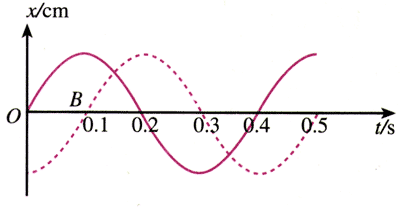
2．图11.2-5是两个简谐运动的振动图象，它们的相位差是多少？

3．有甲、乙两个简谐运动：甲的振幅为2 cm，乙的振幅为3 cm，它们的周期都是4 s，当t＝0时甲的位移为2 cm，乙的相位比甲落后\(\frac{\pi }{4}\)。请在同一坐标系中作出这两个简谐运动的位移—时间图象。

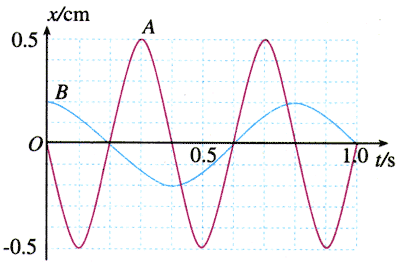
4．图11.2-6为A、B两个简谐运动的位移-时间图象。请根据图象写出这两个简谐运动的位移随时间变化的关系式。

发布时间：2017/1/4 上午10:55:56  阅读次数：1795