第十一章 1 简谐振动
科学是一种方法,它教导人们:一些事物是如何被了解的,不了解的还有些什么,对于了解的,现在了解到了什么程度……
——费恩曼[1]

人类生活在运动的世界里,机械运动是最常见的运动。在机械运动中,除了平动和转动之外,振动也是一种常见的运动。琴弦的振动,让人们欣赏到优美的音乐;地震则可能给人类带来巨大的灾难。然而,振动并不限制在机械运动范围之内,在交流电路中电流和电压的变化,也是一种振动。振动现象,比比皆是。
我门将从最简单的情况出发,学习怎样描述振动,振动有什么性质。
第十一章 1 简谐振动
振动现象在自然界中广泛存在。钟摆的摆动、水中浮标的上下浮动、担物行走时扁担下物体的颤动、树梢在微风中的摇摆……都是振动,一切发声的物体都在振动,地震是大地的剧烈振动,振动与我们的生活密切相关。
弹簧振子
如图11.1-1所示,把一个有孔的小球装在弹簧的一端,弹簧的另一端固定,小球穿在光滑的杆上,能够自由滑动,两者之间的摩擦可以忽略,弹簧的质量与小球相比也可以忽略。把小球拉向右方,然后放开,它就左右运动起来。小球原来静止时的位置叫做平衡位置(equilibrium position),小球在平衡位置附近的往复运动,是一种机械振动,简称振动(vibration)。这样的系统称为弹簧振子(spring oscillator)。
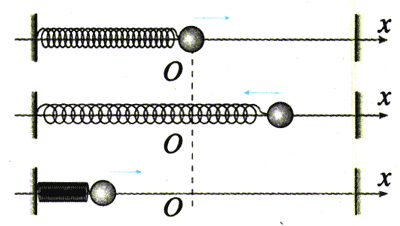
弹簧振子是小球和弹簧所组成的系统的名称,但有时也把这样的小球称做弹簧振子或简称振子。
弹簧振子的位移-时间图象
为了研究弹簧振子的运动规律,我们以小球的平衡位置为坐标原点O,沿着它的振动方向建立坐标轴。小球在平衡位置的右边时它对平衡位置的位移为正,在左边时为负。
本书以后研究振动时所说的位移,都是对于平衡位置的位移。因此,书中字母x具有双重意义:它即表示小球的位置(坐标),又表示小球的位移。
图11.1-2是图11.1-1所示的弹簧振子的频闪照片。频闪仪每隔0.05 s闪光一次,闪光的瞬间振子被照亮。拍摄时底片从下向上匀速运动,因此在底片上留下了小球和弹簧的一系列的像,相邻两个像之间相隔0.05 s。

图11.1-2中的两个坐标轴分别代表时间t和小球位移x,因此它就是小球在平衡位置附近往复运动时的位移-时间图象,即x-t图象。
做一做
用数码相机和计算机绘制小球运动的x-t图象
图11.1-2的照片是通过频闪摄影得到的。使用数码相机和计算机也能得到类似的图片。
弹簧的下端悬挂一个钢球,上端固定,它们组成了一个振动系统。用手把钢球向上托起一段距离,然后释放,钢球便上下振动。钢球原来静止时的位置就是振动的平衡位置(图11.1-3)。
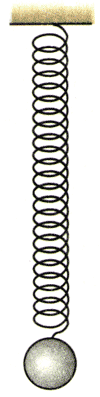
用摄像机或数码照相机拍摄钢球的运动。大约每隔0.04 s数码相机就会拍摄一帧照片。拍摄时最好把钢球的位置放在取景框的最左侧。
在电脑中建立一个幻灯片的演示文稿,把这些照片插入文稿中的同一张空白幻灯片中,照片会按拍摄时间的先后一帧一帧自动向右平铺开来。把这些照片的上端对齐,便能得到与图11.1-2相似的画面。这样就可以在同一个画面上看到钢球在各个不同时刻的位置。
简谐运动及其图象
我们对弹簧振子的位移与时间的关系做些深入的研究。从图11.1-2可以看出,小球运动时的位移与时间的关系很像正弦函数的关系。是不是这样呢?
思考与讨论
确定弹簧振子的位移与时间的关系
方法一
数学课中我们已经学过正弦函数的振幅、周期(频率)等知识。假定图11.1-2中的曲线的确是正弦曲线,用刻度尺测量它的振幅和周期,写出具有这样振幅、周期的正弦函数的表达式。应该注意到,这个表达式中计时开始时位移应该是零,随后位移开始增加并为正值。
然后,在图11.1-2的曲线中选小球的若干个位置,用刻度尺在图中测量它们的横坐标和纵坐标,代入你所写出的正弦函数的表达式中进行检验,看一看这条曲线是否真的是一条正弦曲线。
方法二
在图11.1-2中,测量小球在各个位置的横坐标和纵坐标。把测量值输入计算机中,用数表软件作出这条曲线,看一看弹簧振子的位移一时间的关系可以用什么函数表示。
如果质点的位移与时间的关系遵从正弦函数的规律,即它的振动图象(x-t图象)是一条正弦曲线[2],这样的振动叫做简谐运动(simple harmonic motion)。简谐运动是最简单、最基本的振动。图11.1-1中的弹簧振子的运动就是简谐运动。
做一做
在弹簧振子的小球上安装一枝绘图笔,让一条纸带在与小球振动方向垂直的方向上匀速运动,笔在纸带上画出的就是小球的振动图象(图11.1-4)。
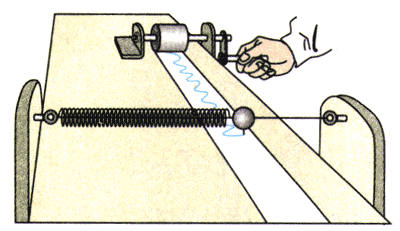
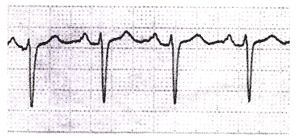
这种记录振动的方法在实际中有很多应用。医院里的心电图仪(图11.1-5)、地震仪中绘制地震曲线的装置(图11.1-6)等,都用类似的方法记录振动情况。

做一做
用传感器和计算机描绘简谐运动
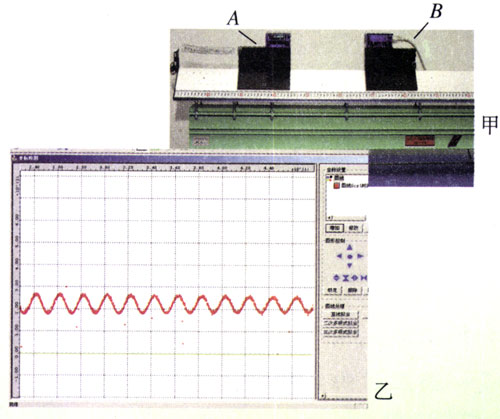
如图11.1-7甲,气垫导轨上的滑块系在一端固定的弹簧上,可以沿导轨做简谐运动。位移传感器的A、B两个小盒分别固定在滑块上和气垫导轨上。B盒通过数据采集器与计算机相连,把各个时刻滑块的位置输入计算机。计算机对数据进行处理后在屏幕上作出滑块的x-t图象(图11.1-7乙)。
问题与练习
1.除了课文中介绍的心电图仪、地震仪之外,你还见过哪些绘制振动曲线的装置?请举出一个实例,并说明:这个实例中绘图笔尖的位移跟时间的关系是不是具有简谐运动的规律?为什么?
2.如图11.1-8,两人合作,模拟振动曲线的记录装置。先在白纸中央画一条直线OO1使它平行于纸的长边,作为图象的横坐标轴。一个人用铅笔尖在白纸上沿垂直于OO1的方向振动,另一个人沿OO1的方向匀速拖动白纸,纸上就画出了一条描述笔尖振动情况的x-t图象。
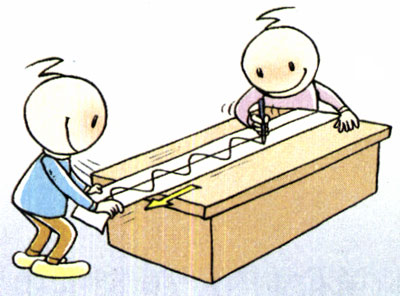
请完成这个实验,并解释:白纸上OO1坐标轴上的坐标代表什么物理量?纵坐标代表什么物理量?为什么必须匀速拖动白纸?如果拖动白纸的速度是5×10-2 m/s,在OO1坐标轴上应该怎样标出时间的坐标刻度?
3.图11.1-9是某质点做简谐运动的振动图象。根据图象中的信息,回答下列问题。
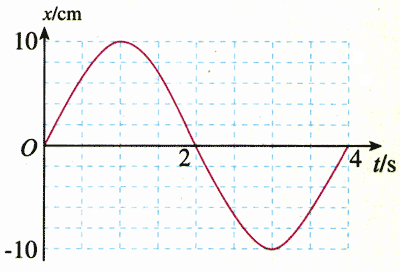
(1)质点离开平衡位置的最大距离有多大?
(2)在1.5 s和2.5 s这两个时刻,质点的位置各在哪里?
(3)在1.5 s和2.5 s这两个时刻,质点向哪个方向运动?
4.如图11.1-9,在t=0到t=4 s的范围内回答以下问题。
(1)质点相对平衡位置的位移方向在哪些时间内跟它瞬时速度的方向相同?在哪些时间内跟瞬时速度的方向相反?
(2)质点在第2 s末的位移是多少?
(3)质点在前2 s内走过的路程是多少?
[1] 理查德·费恩曼(R.P.Feynman,1918 - 1988),美国物理学家,杰出的物理学教育家,由于在量子电动力学方面的贡献而获得1965年诺贝尔物理学奖。
[2] 正弦函数的一般形式是y=Asin(ωx+φ),它的图象叫做正弦曲线,例如y=sin x,y=sin(x+\(\frac{\pi }{4}\))的图象,都是正弦曲线。y=cos x的图象也是一条正弦曲线,因为它可以写成y=sin(x+\(\frac{\pi }{2}\))。
发布时间:2017/1/3 下午2:38:22 阅读次数:4561
