第七章 8 机械能守恒定律

演示

如图7.8-1，一个用细线悬挂的小球从A点开始摆动。记住它向右能够达到的最大高度。然后用一把直尺在P点挡住悬线，看一看这种情况下小球所能达到的最大高度。

如果从能量的角度分析这个现象，你认为实验说明了什么？

动能与势能的相互转化

物体自由下落或沿光滑斜面滑下时，重力对物体做正功，物体的重力势能减少。减少的重力势能到哪里去了？我们发现，在这些过程中，物体的速度增加了，表示物体的动能增加了。这说明，物体原来的重力势能转化成了动能。

原来具有一定速度的物体，由于惯性在空中竖直上升或沿光滑斜面上升，这时重力做负功，物体的速度减小，表示物休的动能减少了。但由于物体的高度增加，它的重力势能增加了。这说明，物体原来具有的动能转化成了重力势能。

不仅重力势能可以与动能相互转化，弹性势能也可以与动能相互转化。被压缩的弹簧具有弹性势能，当弹簧恢复原来形状时，就把跟它接触的物体弹出去。这一过程中，弹力做正功，弹簧的弹性势能减少，而物体得到一定的速度，动能增加。射箭时弓的弹性势能减少，箭的动能增加，也是这样一种过程。

动能转化为重力势能或弹性势能时，重力或弹力做负功。你能举出这样的例子吗？

从上面的讨论可以看到，重力势能、弹性势能与动能之间具有密切的联系，我们把它们统称为机械能（mechanical energy）。通过重力或弹力做功，机械能可以从一种形式转化成另一种形式。

机械能守恒定律

动能与势能的相互转化是否存在某种定量的关系？这里以动能与重力势能的相互转化为例，讨论这个问题。

我们讨论物体只受重力的情况，如自由落体运动或各种抛体运动；或者虽受其他力，但其他力并不做功，如物体沿图7.8-3所示光滑曲面滑下的情形。一句话，在我们所研究的情形里，只有重力做功。

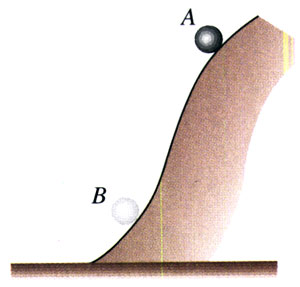
在图7.8-3中，物体在某一时刻处在位置A，这时它的动能是E_k1，重力势能是E_p1，总机械能是E₁＝E_k1＋E_p1。经过一段时间后，物体运动到另一位置B，这时它的动能是E_k2，重力势能是E_p2，总机械能是E₂＝E_k2＋E_p2。

以W表示这一过程中重力做的功。从动能定理知道，重力对物体做的功等于物体动能的增加，即

W＝E_k2－E_k1

另一方面，从重力的功与重力势能的关系知道，重力对物体做的功等于重力势能的减少（见本章第4节“重力势能”），即

W＝E_p1－E_p2

从以上两式可得

E_k2－E_k1＝E_p1－E_p2

移项后，有

E_k2＋E_p2＝E_k1＋E_p1

即

E₂＝E₁

可见，在只有重力做功的物体系统内，动能与重力势能可以互相转化，而总的机械能保持不变。

同样可以证明，在只有弹力做功的物体系统内，动能和弹性势能可以互相转化，总的机械能也保持不变。

我们的结论是：在只有重力或弹力做功的物体系统内，动能与势能可以互相转化，而总的机械能保持不变。这叫做机械能守恒定律（law of conservation of mechanical energy）。它是力学中的一条重要定律，是普遍的能量守恒定律的一种特殊情况。

例题

把一个小球用细线悬挂起来，就成为一个摆（图7.8-5），摆长为l，最大偏角为θ。如果阻力可以忽略，小球运动到最低位置时的速度是多大？

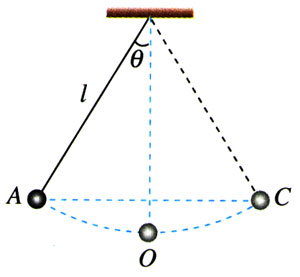
【分析】在阻力可以忽略的情况下，小球摆动过程中受重力和细线的拉力。细线的拉力与小球的运动方向垂直，不做功，所以这个过程中只有重力做功，机械能守恒。

小球在最高点只有重力势能，没有动能，计算小球在最高点和最低点重力势能的差值，根据机械能守恒定律就能得出它在最低点的动能，从而算出它在最低点的速度。

【解】把最低点的重力势能定为0，以小球在最高点的状态作为初状态。在最高点的重力势能是E_p1＝mg（l－lcosθ），而动能为0，即E_k1＝0。

小球在最高点与最低点的高度差为l－lcosθ，这个关系可以由几何关系得出。

以小球在最低点的状态作为末状态，势能E_p2＝0，而动能可以表示为E_k2＝\(\frac{1}{2}\)mv²。

运动过程中只有重力做功，所以机械能守恒，即

E_k2＋E_p2＝E_k1＋E_p1

把各个状态下动能、势能的表达式代入，得

\(\frac{1}{2}\)mv²＝mg（l－lcosθ）

由此解出

v＝\(\sqrt {2gl(1 - \cos \theta )} \)

从得到的表达式可以看出，初状态的θ角越大，cosθ越小，（1－cosθ）就越大，v也就越大。也就是说，最初把小球拉得越高，它到达最下端时的速度也就越大。这与生活经验是一致的。

解决一个问题之后要对结论进行分析。如果与已有的知识或日常经验不一致，则要认真考虑，看看是否出现了错误。这就是我们所说的“评估”。

从这个例题可以看出，应用机械能守恒定律解决问题，只需考虑运动的初状态和末状态，不必考虑两个状态间过程的细节。如果直接用牛顿定律解决问题，需要分析过程中各种力的作用，而这些力又往往在变化着，因此一些难于用牛顿定律解决的问题，应用机械能守恒定律则易于解决。

思考与讨论

一个小球在真空中自由下落，另一个同样的小球在黏性较大的液体中由静止开始下落。它们都由高度为h₁的地方下落到高度为h₂的地方。在这两种情况下，重力做的功相等吗？重力势能的变化相等吗？动能的变化相等吗？重力势能各转化成什么形式的能？

问题与练习

1．如图7.8-6，质量为m的小球从光滑曲面上滑下。当到达高度为h₁的位置A时，速度的大小为v₁，滑到高度为h₂的位置B时，速度的大小为v₂。在由高度h₁滑到高度h₂的过程中，重力做的功为W。

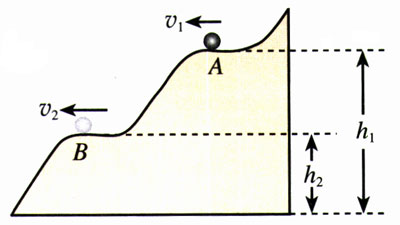
（1）根据动能定理列出方程，描述小球在A、B两点间动能的关系。

（2）根据重力做功与重力势能的关系，把以上方程变形，以反映出小球运动过程中机械能是守恒的。

2．神舟号载人飞船在发射至返回的过程中，以下哪些阶段中返回舱的机械能是守恒的？

A．飞船升空的阶段。

B．飞船在椭圆轨道上绕地球运行的阶段。

C．返回舱在大气层以外向着地球做无动力飞行的阶段。

D．降落伞张开后，返回舱下降的阶段。

3．把质量为0.5 kg的石块从10 m高处以30°角斜向上方抛出（图7.8-7），初速度是v₀＝5 m/s。不计空气阻力。

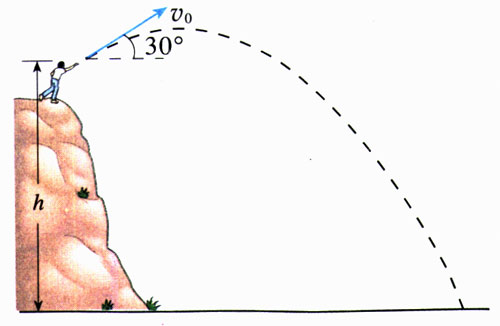
（1）石块落地时的速度是多大？请用机械能守恒定律和动能定理分别讨论。

（2）石块落地时速度的大小与下列哪些量有关，与哪些量无关？说明理由。

A．石块的质量。

B．石块初速度的大小。

C．石块初速度的仰角。

D．石块抛出时的高度。

4．有一种地下铁道，车站的路轨建得高些，车辆进站时要上坡，出站时要下坡，如图7.8-8。设坡高h为2 m，进站车辆到达坡下的A点时，速度为25.2 km/h，此时切断电动机的电源，车辆能不能“冲”到坡上？如果能够，到达坡上的速度是多大？

发布时间：2016/12/21 上午11:35:45  阅读次数：3013