第七章 7 动能和动能定理

动能的表达式

通过上节的实验，我们已经了解到一个特殊情形下力对物体做的功与物体速度变化的关系，即W∝v²。根据做功与能量变化相关联的思想，这个结果实际上向我们提示：物体动能的表达式中可能包含v²这个因子。本节我们再沿另一条线索探索物体动能的表达式，如果两者能够相互支持，做结论时就多一分把握。

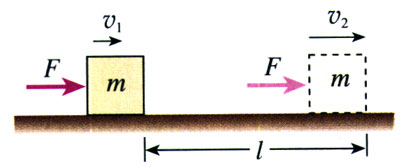
设某物体的质量为m，在与运动方向相同的恒力F的作用下发生一段位移l，速度由v₁增加到v₂，如图7.7-1所示。这个过程中力F做的功W＝Fl。

根据牛顿第二定律

F＝ma

而v₂²－v₁²＝2al，即

l＝\(\frac{{v_2^2 - v_1^2}}{{2a}}\)

v₂²－v₁²＝2al是匀变速运动的规律。这个物体的运动是匀变速运动吗？

把F、l的表达式代入W＝Fl，可得F做的功

W＝\(\frac{{ma(v_2^2 - v_1^2)}}{{2a}}\)

也就是

W＝\(\frac{1}{2}\)mv₂²－\(\frac{1}{2}\)mv₁²

从这个式子可以看出，“\(\frac{1}{2}\)mv²”很可能是一个具有特定意义的物理量，因为这个量在过程终了与过程开始时的差，正好等于力对物体做的功，所以“\(\frac{1}{2}\)mv²”应该就是我们寻找的动能表达式。上节的实验已经表明，力对初速度为0的物体所做的功与物体速度的二次方成正比，这也印证了我们的想法。于是我们说，质量为m的物体，以速度v运动时的动能是

E_k＝\(\frac{1}{2}\)mv²                          （1）

动能也是标量，它的单位与功的单位相同，在国际单位制中都是焦耳，这是因为1 kg·m²/s²＝1 N·m＝1 J。

我国在1970年发射的第一颗人造地球卫星，质量为173 kg，运动速度为7.2 km/s，它的动能是

E_k＝\(\frac{1}{2}\)mv²＝\(\frac{1}{2}\)×173×（7.2×10³）² J ＝4.5×10⁹ J

动能定理

在得到动能的表达式后，W＝\(\frac{1}{2}\)mv₂²－\(\frac{1}{2}\)mv₁²可以写成

W＝E_k2－E_k1                       （2）

其中E_k2表示一个过程的末动能\(\frac{1}{2}\)mv₂²，E_k1表示这个过程的初动能\(\frac{1}{2}\)mv₁²。

这个关系表明，力在一个过程中对物体做的功，等于物体在这个过程中动能的变化。这个结论叫做动能定理（theorem of kinetic energy）。

如果物体受到几个力的共同作用，动能定理中的W即为合力做的功，它等于各个力做功的代数和。例如，一架飞机在牵引力和阻力的共同作用下，在跑道上加速运动，速度越来越大，动能也就越来越大。牵引力和阻力的合力做了多少功，飞机的动能就增加多少。

本书中，动能定理是在物体受恒力作用，并且做直线运动的情况下得到的。当物体受变力作用，或做曲线运动时，我们仍可采用过去的方法，把过程分解成许多小段，认为物体在每小段运动中受到的是恒力，运动的轨迹是直线，这样也能得到动能定理。

正因为动能定理适用于变力做功和曲线运动的情况，所以在解决一些实际的力学问题时，它得到了广泛的应用。

例题1

一架喷气式飞机，质量m＝5.0×10³ kg，起飞过程中从静止开始滑跑。当位移达到l＝5.3×10² m时，速度达到起飞速度v＝60 m/s。在此过程中飞机受到的平均阻力是飞机重量的0.02倍。求飞机受到的牵引力。

【分析】滑跑过程中牵引力与阻力的合力对飞机做功。本题已知飞机滑跑过程的始末速度，因而能够知道它在滑跑过程中增加的动能，故可应用动能定理求出合力做的功，进而求出合力、牵引力。

【解】飞机的初动能E_k1＝0，末动能E_k2＝\(\frac{1}{2}\)mv²；合力F做的功W＝Fl。

根据动能定理，W＝E_k2－E_k1，于是有

Fl＝\(\frac{1}{2}\)mv²－0

合力F为牵引力F_牵与阻力F_阻之差，而阻力与飞机重量的关系为F_阻＝kmg（其中k＝0.02），所以

F＝F_牵－kmg

代入上式后解出

F_牵＝\(\frac{{m{v^2}}}{{2l}}\)＋kmg

把数值代入后得到

F_牵＝1.8×10⁴ N

飞机所受的牵引力是1.8×10⁴ N。

飞机滑行时除了地面阻力外，还受到空气阻力，后者随速度的增加而增加。本题说“平均阻力是飞机重量的0.02倍”，只是一种粗咯的估算。

从这个例题可以看出，动能定理不涉及物体运动过程中的加速度和时间，因此用它处理问题常常比较方便。

在应用动能定理时还应该注意到，力对物体做的功可正可负。做正功时物体的动能增加，做负功时物体的动能减少。

例题2

一辆质量为m、速度为v₀的汽车，关闭发动机后在水平地面上滑行了距离l后停了下来（图7.7-3）。试求汽车受到的阻力。

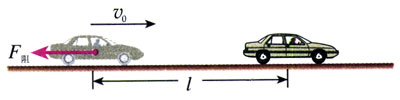
【分析】我们讨论的是汽车从关闭发动机到静止的运动过程。这个过程的初动能、末动能都可以求出，因而应用动能定理可以知道阻力做的功，进而求出汽车受到的阻力。

汽车实际上受到的阻力F_阻是变化的。这里以F_阻l表示阻力做的功，求出的F_阻是汽车在这段距离中受到的平均阻力。

【解】汽车的初动能、末动能分别为\(\frac{1}{2}\)mv₀²和0，阻力F_阻做的功为－F_阻l。应用动能定理，有

－F_阻l＝0－\(\frac{1}{2}\)mv₀²

由此解出

F_阻＝\(\frac{{mv_0^2}}{{2l}}\)

汽车在这段运动中受到的阻力是\(\frac{{mv_0^2}}{{2l}}\)。

能不能用牛顿运动定律解决这个问题？试一试。

思考与讨论

做功的过程是能量从一种形式转化为另一种形式的过程，或从一个物体转移到另一个物体的过程。在上面的例题中，阻力做功，汽车的动能到哪里去了？

问题与练习

1．改变汽车的质量和速度，都可能使汽车的动能发生改变。在下列几种情形下，汽车的动能各是原来的几倍？

A．质量不变，速度增夫到原来的2倍。

B．速度不变，质量增大到原来的2倍。

C．质量减半，速度增大到原来的4倍。

D．速度减半，质量增大到原来的4倍。

2．把一辆汽车的速度从10 km/h加速到20 km/h，或者从50 km/h加速到60 km/h，哪种情况做的功比较多？通过计算说明。

3．质量是2g的子弹，以300 m/s的速度射入厚度是5 cm的木板（图7.7-4），射穿后的速度是100 m/s。子弹射穿木板的过程中受到的平均阻力是多大？

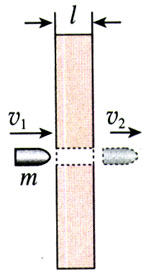
你对题目中所说的“平均”一词有什么认识？

4．我们在第四章曾用牛顿运动定律解答过一个问题：民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面，若斜面高3.2 m，斜面长6.5 m，质量60 kg的人沿斜面滑下时所受的阻力是240N，求人滑至底端时的速度。请用动能定理解答本题。

5．运动员把质量是500 g的足球踢出后，某人观察它在空中的飞行情况，估计上升的最大高度是10 m，在最高点的速度为20 m/s。请你根据这个估计，计算运动员踢球时对足球做的功。

发布时间：2016/12/20 上午9:23:02  阅读次数：1952